
História do Princípio de Pascal, aplicações, exemplos
O Princípio de Pascal, ou a lei de Pascal, estabelece que uma mudança na pressão de um fluido confinado em qualquer um de seus pontos é transmitida sem alteração para todos os outros pontos dentro do fluido.
Este princípio foi descoberto pelo cientista francês Blaise Pascal (1623 - 1662). Devido à importância das contribuições de Pascal para a ciência, a unidade de pressão do Sistema Internacional foi nomeada em sua homenagem..

Uma vez que a pressão é definida como a razão entre a força perpendicular a uma superfície e sua área, 1 Pascal (Pa) é igual a 1 newton / mdois.
Índice do artigo
- 1 história
- 2 Explicação do princípio de Pascal
- 2.1 A relação entre pressão e profundidade
- 3 aplicativos
- 3.1 A prensa hidráulica
- 4 exemplos
- 4.1 Freios hidráulicos
- 4.2 Vantagem mecânica da prensa hidráulica
- 5 Exercício resolvido
- 6 referências
História
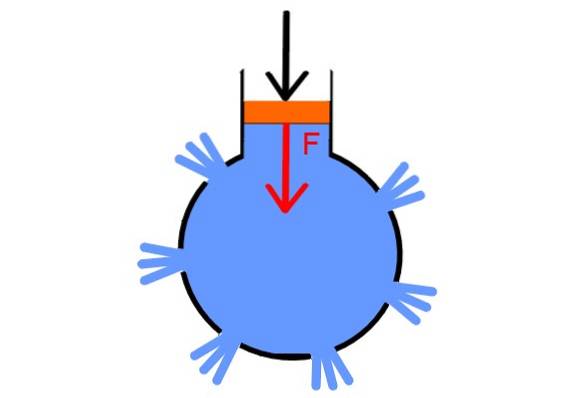
Para testar seu princípio, Pascal inventou uma prova bastante convincente. Ele pegou uma esfera oca e perfurou em vários lugares, colocou tampões em todos os orifícios exceto um, através do qual ele a encheu com água. Neste ele colocou uma seringa equipada com um êmbolo.
Ao aumentar suficientemente a pressão no êmbolo, os plugues são liberados ao mesmo tempo, pois a pressão é transmitida igualmente para todos os pontos do fluido e em todas as direções, demonstrando assim a lei de Pascal.
Blaise Pascal teve uma vida curta, marcada pela doença. O incrível alcance de sua mente o levou a investigar vários aspectos da natureza e da filosofia. Suas contribuições não se limitaram a estudar o comportamento dos fluidos, Pascal também foi um pioneiro da computação.
E é que, aos 19 anos, Pascal criou uma calculadora mecânica para seu pai usar em seu trabalho no sistema tributário francês: o pascalina.
Além disso, junto com seu amigo e colega o grande matemático Pierre de Fermat, eles moldaram a teoria das probabilidades, indispensável na Física e na Estatística. Pascal faleceu em Paris, aos 39 anos.
Explicação do princípio de Pascal
O seguinte experimento é bastante simples: um tubo em U é preenchido com água e tampões são colocados em cada extremidade que podem deslizar suave e facilmente, como os pistões. Faz-se pressão contra o pistão esquerdo, afundando-o um pouco e observa-se que o pistão direito sobe, empurrado pelo fluido (figura abaixo).
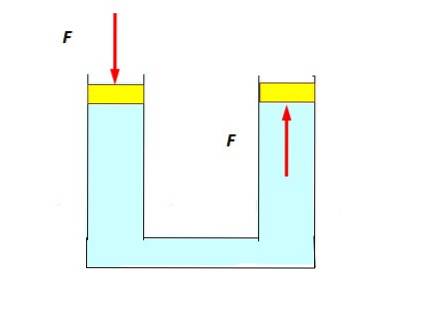
Isso ocorre porque a pressão é transmitida sem diminuição para todos os pontos do fluido, inclusive aqueles que estão em contato com o pistão à direita..
Líquidos como água ou óleo são incompressíveis, mas ao mesmo tempo as moléculas têm liberdade de movimento suficiente, o que permite que a pressão seja distribuída no pistão correto..
Graças a isso, o pistão direito recebe uma força que é exatamente igual em magnitude e direção à aplicada à esquerda, mas na direção oposta..
A pressão em um fluido estático é independente do formato do recipiente. Será mostrado em breve que a pressão varia linearmente com a profundidade e o princípio de Pascal é uma consequência disso..
Uma mudança na pressão em qualquer ponto faz com que a pressão em outro ponto mude na mesma quantidade. Caso contrário, haveria uma pressão extra que faria o líquido fluir.
A relação entre pressão e profundidade
Um fluido em repouso exerce uma força nas paredes do recipiente que o contém e também na superfície de qualquer objeto imerso nele. No experimento da seringa de Pascal, é visto que os jatos de água saem perpendicularmente para a esfera.
Os fluidos distribuem a força perpendicularmente sobre a superfície sobre a qual atua, por isso é conveniente introduzir o conceito de pressão média. Pm como a força perpendicular exercida F⊥ Por área PARA, cuja unidade SI é o pascal:
Pm = F⊥ / PARA
A pressão aumenta com a profundidade. Isso pode ser visto isolando uma pequena porção de fluido em equilíbrio estático e aplicando a segunda lei de Newton:
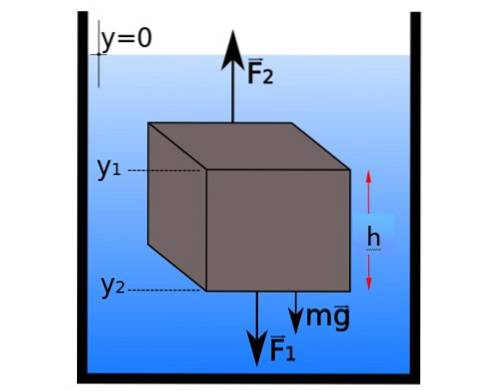
As forças horizontais se cancelam aos pares, mas na direção vertical as forças são agrupadas assim:
∑FY = Fdois - F1 - mg = 0 → Fdois - F1 = mg
Expressando massa em termos de densidade ρ = massa / volume:
Pdois.A- P1.A = ρ x volume x g
O volume da porção de fluido é o produto A x h:
A. (Pdois - P1) = ρ x A x h x g
ΔP = ρ.g.h Teorema fundamental da hidrostática
Formulários

O princípio de Pascal foi usado para construir vários dispositivos que multiplicam a força e facilitam tarefas como levantar pesos, estampar metal ou prensar objetos. Entre eles estão:
-A prensa hidráulica
-O sistema de travagem do carro
-Pás mecânicas e braços mecânicos
-O macaco hidráulico
-Guindastes e elevadores
A seguir, vamos ver como o princípio de Pascal transforma pequenas forças em grandes forças para fazer todas essas tarefas. A prensa hidráulica é o exemplo mais característico e será analisada a seguir.
A prensa hidráulica

Para construir uma prensa hidráulica, toma-se o mesmo dispositivo da figura acima, ou seja, um recipiente em forma de U, do qual já sabemos que a mesma força é transmitida de um pistão para o outro. A diferença será o tamanho dos pistões e é isso que faz o dispositivo funcionar.
A figura a seguir mostra o princípio de Pascal em ação. A pressão é a mesma em todos os pontos do fluido, tanto no pistão pequeno quanto no grande:
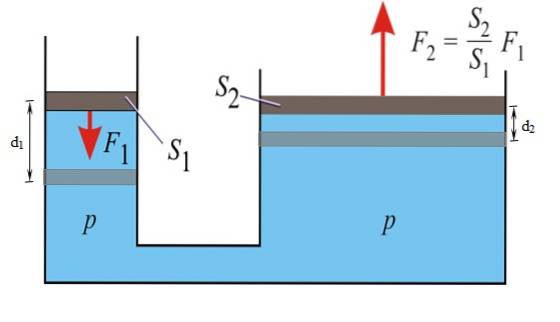
p = F1 / S1 = Fdois / Sdois
A magnitude da força transmitida ao pistão grande é:
Fdois = (Sdois / S1) F1
Como Sdois > S1, resultados em Fdois > F1, portanto, a força de saída foi multiplicada pelo fator dado pelo quociente entre as áreas.
Exemplos
Esta seção apresenta exemplos de aplicação.
Freios hidráulicos
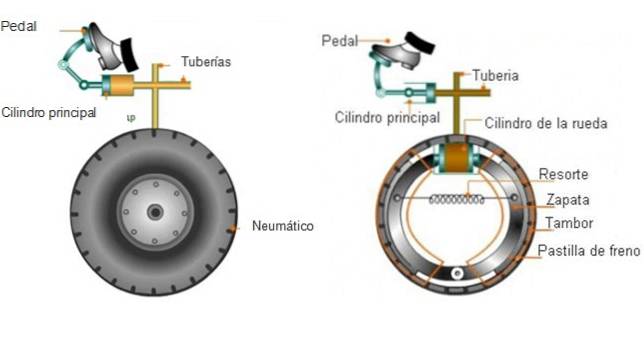
Os freios do carro fazem uso do princípio de Pascal por meio de um fluido hidráulico que preenche tubos conectados às rodas. Quando ele precisa parar, o motorista aplica uma força pressionando o pedal do freio e criando pressão de fluido.
No outro extremo, a pressão empurra as pastilhas de freio contra o tambor ou discos de freio que giram em conjunto com as rodas (não os pneus). O atrito resultante faz com que o disco pare, também diminuindo a velocidade das rodas.
Vantagem Mecânica da Prensa Hidráulica
Na prensa hidráulica da figura abaixo, o trabalho de entrada deve ser igual ao trabalho de saída, desde que o atrito não seja levado em consideração..

Força de entrada F1 faz o pistão percorrer uma distância d1 diminuindo, enquanto a força de saída Fdois permite um passeio ddois do pistão ascendente. Se o trabalho mecânico realizado por ambas as forças é o mesmo:
F1.d1 = Fdois. ddois
A vantagem mecânica M é o quociente entre as magnitudes da força de entrada e da força de saída:
M = Fdois/ F1 = d1/ ddois
E como demonstrado na seção anterior, também pode ser expresso como o quociente entre as áreas:
Fdois/ F1 = Sdois / S1
Parece que o trabalho pode ser feito de graça, mas na verdade não está sendo gerada energia com este dispositivo, já que a vantagem mecânica é obtida às custas do deslocamento do pequeno pistão d1.
Assim, para otimizar o desempenho, um sistema de válvula é adicionado ao dispositivo de forma que o pistão de saída sobe graças a breves impulsos no pistão de entrada..
Desta forma, o operador de um macaco hidráulico de garagem bombeia várias vezes para levantar gradualmente um veículo..
Exercício resolvido
Na prensa hidráulica da Figura 5, as áreas do pistão são de 0,5 polegadas quadradas (pistão pequeno) e 25 polegadas quadradas (pistão grande). Achar:
a) A vantagem mecânica desta prensa.
b) A força necessária para levantar uma carga de 1 tonelada.
c) A distância que a força de entrada deve atuar para levantar a referida carga em 1 polegada.
Expresse todos os resultados em unidades do sistema britânico e do Sistema Internacional SI.
Solução
a) A vantagem mecânica é:
M = Fdois/ F1 = Sdois/ S1 = 25 poldois / 0,5 pol.dois = 50
b) 1 tonelada é igual a 2.000 lb-força. A força necessária é F1:
F1 = Fdois / M = 2.000 lb-força / 50 = 40 lb-força
Para expressar o resultado no Sistema Internacional, é necessário o seguinte fator de conversão:
1 lb-força = 4.448 N
Portanto, a magnitude de F1 é 177,92 N.
c) M = d1/ d2 → d1 = M.ddois = 50 x 1 pol. = 50 pol.
O fator de conversão necessário é: 1 in = 2,54 cm
d1 = 127 cm = 1,27 m
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill. 417-450.
- Física da faculdade. Pascal começou. Recuperado de: opentextbc.ca.
- Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 4. Fluidos e termodinâmica. Editado por Douglas Figueroa (USB). 4 - 12.
- Rex, A. 2011. Fundamentals of Physics. Pearson. 246-255.
- Tippens, P. 2011. Physics: Concepts and Applications. 7ª Edição. McGraw Hill. 301-320.



Ainda sem comentários