UMA prisma trapezoidal é um prisma tal que os polígonos envolvidos são trapézios. A definição de um prisma é um corpo geométrico tal que é formado por dois polígonos iguais e paralelos e o resto de suas faces são paralelogramos.
Um prisma pode ter diferentes formas, que dependem não apenas do número de lados do polígono, mas do próprio polígono.
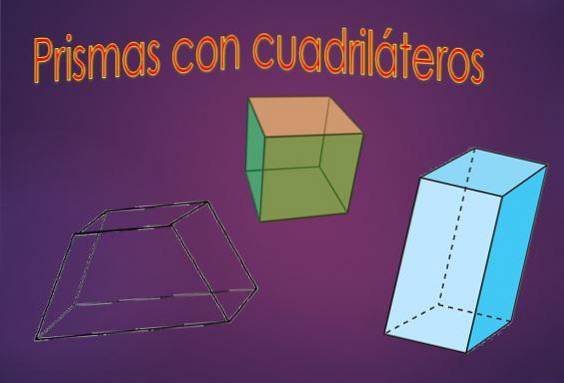
Se os polígonos envolvidos em um prisma são quadrados, isso é diferente de um prisma envolvendo losangos, por exemplo, embora ambos os polígonos tenham o mesmo número de lados. Portanto, depende de qual quadrilátero está envolvido..
Para ver as características de um prisma trapezoidal, você deve começar sabendo como ele é desenhado, então quais propriedades a base cumpre, qual é a área de superfície e finalmente como seu volume é calculado.
Para desenhá-lo, é necessário primeiro definir o que é um trapézio.
Um trapézio é um polígono irregular com quatro lados (quadrilátero), de forma que possui apenas dois lados paralelos chamados bases e a distância entre suas bases é chamada de altura..
Para desenhar o prisma trapezoidal reto, comece desenhando um trapézio. Em seguida, uma linha vertical de comprimento "h" é projetada a partir de cada vértice e, finalmente, outro trapézio é desenhado de forma que seus vértices coincidam com as extremidades das linhas previamente traçadas..
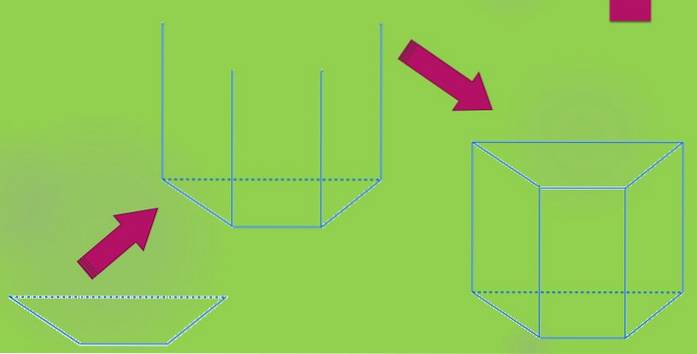
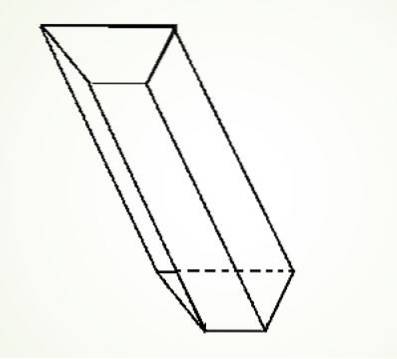
Também pode ter um prisma trapezoidal oblíquo, cuja construção é semelhante à anterior, bastando desenhar as quatro linhas paralelas entre si.
Como afirmado antes, a forma do prisma depende do polígono. No caso particular do trapézio, podemos encontrar três tipos diferentes de bases:
-Trapézio retângulo: é aquele trapézio tal que um de seus lados é perpendicular aos seus lados paralelos ou que simplesmente tem um ângulo reto.
-Trapézio isósceles: é um trapézio tal que seus lados não paralelos têm o mesmo comprimento.
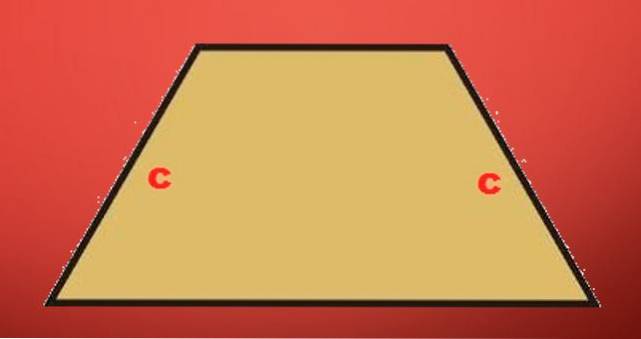
Trapézio escaleno: é aquele trapézio que não é isósceles ou retângulo; seus quatro lados têm comprimentos diferentes.
Como pode ser visto, de acordo com o tipo de trapézio utilizado, será obtido um prisma diferente.
Para calcular a área da superfície de um prisma trapezoidal, precisamos saber a área do trapézio e a área de cada paralelogramo envolvido..
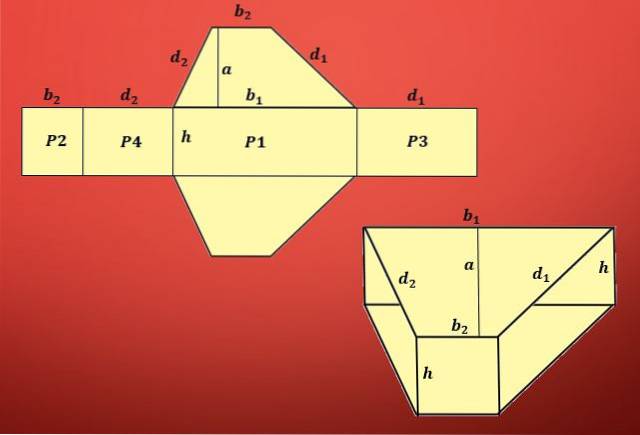
Como pode ser visto na imagem anterior, a área envolve dois trapézios e quatro paralelogramos diferentes..
A área de um trapézio é definida como T = (b1 + b2) xa / 2 e as áreas dos paralelogramos são P1 = hxb1, P2 = hxb2, P3 = hxd1 e P4 = hxd2, onde “b1” e “b2 ”São as bases do trapézio,“ d1 ”e“ d2 ”os lados não paralelos,“ a ”é a altura do trapézio e“ h ”a altura do prisma.
Portanto, a área de superfície de um prisma trapezoidal é A = 2T + P1 + P2 + P3 + P4.
Como o volume de um prisma é definido como V = (área do polígono) x (altura), pode-se concluir que o volume de um prisma trapezoidal é V = Txh.
Um dos objetos mais comuns que têm a forma de um prisma trapezoidal é um lingote de ouro ou as rampas usadas em corridas de moto..
Ainda sem comentários