
Conceito de probabilidade de frequência, como é calculado e exemplos
O probabilidade de frequência é uma sub-definição dentro do estudo da probabilidade e seus fenômenos. Seu método de estudo com relação a eventos e atributos é baseado em grandes quantidades de iterações, observando assim a tendência de cada uma no longo prazo ou mesmo em repetições infinitas..
Por exemplo, um envelope de gomas contém 5 borrachas de cada cor: azul, vermelho, verde e amarelo. Queremos determinar a probabilidade de que cada cor saia após uma seleção aleatória.

É tedioso imaginar tirar uma borracha, registrá-la, devolvê-la, tirar uma borracha e repetir a mesma coisa várias centenas ou milhares de vezes. Você pode até querer observar o comportamento após vários milhões de iterações.
Mas, ao contrário, é interessante descobrir que, após algumas repetições, a probabilidade esperada de 25% não é atingida totalmente, pelo menos não para todas as cores após a ocorrência de 100 iterações..
Sob a abordagem da probabilidade de frequência, a atribuição dos valores só se dará por meio do estudo de várias iterações. Desta forma o processo deve ser realizado e registrado preferencialmente de forma informatizada ou emulada.
Múltiplas correntes rejeitam a probabilidade de frequência, argumentando falta de empirismo e confiabilidade nos critérios de aleatoriedade.
Índice do artigo
- 1 Como a probabilidade de frequência é calculada?
- 1.1 Lei dos grandes números
- 2 Outras abordagens de probabilidade
- 2.1 Teoria lógica
- 2.2 Teoria subjetiva
- 3 História
- 3.1 Fenômenos de massa e eventos repetitivos
- 3.2 Atributos
- 4 exemplo
- 4.1 Referências
Como é calculada a probabilidade de frequência?
Ao programar o experimento em qualquer interface capaz de oferecer uma iteração puramente aleatória, pode-se começar a estudar a probabilidade de frequência do fenômeno por meio de uma tabela de valores.
O exemplo anterior pode ser visto a partir da abordagem de frequência:
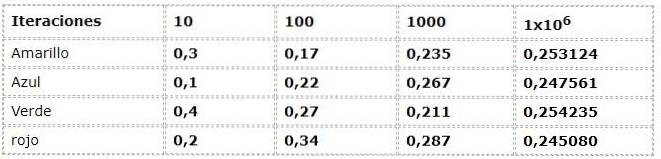
Os dados numéricos correspondem à expressão:
N (a) = Número de ocorrências / Número de iterações
Onde N (a) representa a frequência relativa do evento "a"
"A" pertence ao conjunto de resultados possíveis ou espaço amostral Ω
Ω: vermelho, verde, azul, amarelo
Uma dispersão considerável é apreciada nas primeiras iterações, ao observar frequências com até 30% de diferença entre elas, o que é um dado muito alto para um experimento que teoricamente possui eventos com a mesma possibilidade (Equiprovável).
Mas à medida que as iterações crescem, os valores parecem se ajustar cada vez mais àqueles apresentados pela corrente teórica e lógica.
Lei dos grandes números
Como um acordo inesperado entre as abordagens teórica e de frequência surge a lei dos grandes números. Onde fica estabelecido que após um número considerável de iterações, os valores do experimento de frequência estão se aproximando dos valores teóricos.
No exemplo, você pode ver como os valores se aproximam de 0,250 conforme as iterações aumentam. Este fenômeno é elementar nas conclusões de muitos trabalhos probabilísticos..

Outras abordagens de probabilidade
Existem 2 outras teorias ou abordagens para a noção de probabilidade, além do probabilidade de frequência.
Teoria lógica
Sua abordagem é orientada para a lógica dedutiva dos fenômenos. No exemplo anterior, a probabilidade de obtenção de cada cor é de 25% de forma fechada. Ou seja, suas definições e axiomas não contemplam defasagens fora de sua faixa de dados probabilísticos..
Teoria subjetiva
Baseia-se no conhecimento e nas crenças prévias que cada indivíduo possui sobre os fenômenos e atributos. Declarações como “Sempre chove na Páscoa " Devem-se a um padrão de eventos semelhantes que ocorreram anteriormente.
História
O início de sua implementação remonta ao século 19, quando Venn o citou em várias de suas obras em Cambridge, Inglaterra. Mas não foi até meados do século XX que 2 matemáticos estatísticos desenvolveram e moldaram o probabilidade de frequência.
Um deles foi Hans Reichenbach, que desenvolve seu trabalho em publicações como "The Theory of Probability" publicada em 1949.
O outro foi Richard Von Mises, que desenvolveu seu trabalho por meio de várias publicações e propôs considerar a probabilidade como uma ciência matemática. Este conceito era novo para a matemática e daria início a uma era de crescimento no estudo da matemática. probabilidade de frequência.
Na verdade, este evento marca a única diferença com as contribuições feitas pela geração Venn, Cournot e Helm. Onde a probabilidade se torna homóloga às ciências como geometria e mecânica.
< La teoría de las probabilidades trata con fenômenos massivos e eventos repetitivos. Problemas em que o mesmo evento se repete continuamente, ou um grande número de elementos uniformes estão envolvidos ao mesmo tempo> Richard Von Mises
Fenômenos massivos e eventos repetitivos
Três tipos podem ser classificados:
- Físico: eles obedecem a padrões da natureza além de uma condição de aleatoriedade. Por exemplo, o comportamento das moléculas de um elemento em uma amostra.
- Chance - Sua principal consideração é a aleatoriedade, como jogar um dado repetidamente.
- Estatísticas biológicas: seleções de assuntos de teste de acordo com suas características e atributos.
Em tese, o indivíduo que mede desempenha um papel nos dados probabilísticos, pois são seus conhecimentos e experiências que articulam esse valor ou predição..
No probabilidade de frequência os eventos serão considerados como coleções a serem tratadas, onde o indivíduo não desempenhe qualquer papel na estimativa.
Atributos
Um atributo ocorre em cada elemento, que será variável de acordo com sua natureza. Por exemplo, no tipo de fenômeno físico, as moléculas de água terão velocidades diferentes..
No lançamento dos dados conhecemos o espaço amostral Ω que representa os atributos do experimento.
Ω: 1, 2, 3, 4, 5, 6
Existem outros atributos, como ser uniforme ΩP ou ser estranho Ωeu
Ωp : 2, 4, 6
Ωeu : 1, 3, 5
Que podem ser definidos como atributos não elementares.
Exemplo
- Queremos calcular a frequência de cada soma possível no lançamento de dois dados.
Para isso, é programado um experimento onde duas fontes de valores aleatórios entre [1, 6] são adicionadas a cada iteração.
Os dados são registrados em uma tabela e as tendências em grande número são estudadas.
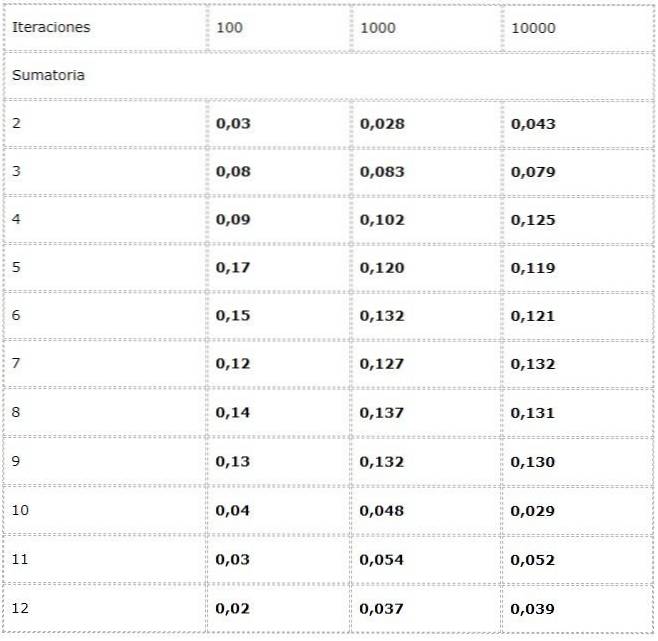
Observa-se que os resultados podem variar consideravelmente entre as iterações. No entanto, a lei dos grandes números pode ser vista na aparente convergência apresentada nas duas últimas colunas..
Referências
- Estatísticas e avaliação de evidências para cientistas forenses. Segunda edição. Colin G.G. Aitken. Escola de Matemática. Universidade de Edimburgo, Reino Unido
- Matemática para Ciência da Computação. Eric Lehman. Google Inc.
F Thomson Leighton Departamento de Matemática e Ciência da Computação e Laboratório de IA, Instituto de Tecnologia de Massachusetts; Akamai Technologies - The Arithmetic Teacher, Volume 29. National Council of Teachers of Mathematics, 1981. University of Michigan.
- Aprendizagem e ensino da teoria dos números: Pesquisa em cognição e instrução / editado por Stephen R. Campbell e Rina Zazkis. Ablex publicando 88 Post Road West, Westport CT 06881
- Bernoulli, J. (1987). Ars Conjectandi- 4ème partie. Rouen: IREM.



Ainda sem comentários