
Bloquear propriedade da prova de álgebra, exemplos
O bloquear propriedade da álgebra é um fenômeno que relaciona dois elementos de um conjunto com uma operação, onde a condição necessária é que, após os 2 elementos serem processados sob a referida operação, o resultado também pertença ao conjunto inicial.
Por exemplo, se os números pares forem tomados como um conjunto e uma soma como uma operação, obteremos um bloqueio desse conjunto em relação à soma. Isso ocorre porque a soma de 2 números pares sempre produzirá outro número par, atendendo assim à condição de bloqueio.

Índice do artigo
- 1 recursos
- 2 álgebra de números
- 3 demo
- 3.1 Soma
- 3.2 Multiplicação
- 4 casos especiais em R
- 4.1 Divisão
- 4.2 Arquivamento
- 4.3 Logaritmo
- 5 exemplos
- 5.1 Soma em N
- 5.2 Subtração em N
- 6 exercícios propostos
- 7 referências
Caracteristicas
Existem muitas propriedades que determinam espaços ou corpos algébricos, como estruturas ou anéis. No entanto, a propriedade de bloqueio é uma das mais conhecidas dentro da álgebra básica.
Nem todas as aplicações dessas propriedades são baseadas em elementos ou fenômenos numéricos. Muitos exemplos do dia a dia podem ser trabalhados a partir de uma abordagem puramente algébrica-teórica.
Um exemplo podem ser os cidadãos de um país que assumem uma relação jurídica de qualquer tipo, como uma parceria comercial ou casamento, entre outros. Depois de realizada esta operação ou gestão, continuam a ser cidadãos do país. Desta forma, as operações de cidadania e gestão em relação a dois cidadãos representam um bloqueio.
Álgebra numérica
No que diz respeito aos números, muitos são os aspectos que têm sido objeto de estudo em diferentes correntes da matemática e da álgebra. Um grande número de axiomas e teoremas emergiu desses estudos que servem como base teórica para pesquisas e trabalhos contemporâneos..
Se trabalharmos com os conjuntos numéricos, podemos estabelecer outra definição válida para a propriedade de bloqueio. Um conjunto A é considerado o bloqueio de outro conjunto B se A for o menor conjunto que contém todos os conjuntos e operações que B abriga..
Demonstração
A prova de bloqueio é aplicada para elementos e operações presentes no conjunto de números reais R.
Sejam A e B dois números pertencentes ao conjunto R, o fechamento desses elementos é definido para cada operação contida em R.
Soma
- Soma: ∀ A ˄ B ∈ R → A + B = C ∈ R
Esta é a maneira algébrica de dizer que Para todos os A e B que pertencem aos números reais, temos que a soma de A mais B é igual a C, que também pertence aos números reais.
É fácil verificar se essa proposição é verdadeira; basta realizar a soma entre qualquer número real e verificar se o resultado também pertence aos números reais.
3 + 2 = 5 ∈ R
-2 + (-7) = -9 ∈ R
-3 + 1/3 = -8/3 ∈ R
5/2 + (-2/3) = 11/6 ∈ R
Observa-se que a condição de bloqueio é atendida para os números reais e a soma. Desta forma, pode-se concluir: A soma dos números reais é uma fechadura algébrica.
Multiplicação
- Multiplicação: ∀ A ˄ B ∈ R → A. B = C ∈ R
Para todos os A e B que pertencem aos reais, temos que a multiplicação de A por B é igual a C, que também pertence aos reais.
Ao verificar com os mesmos elementos do exemplo anterior, os seguintes resultados são observados.
3 x 2 = 6 ∈ R
-2 x (-7) = 14 ∈ R
-3 x 1/3 = -1 ∈ R
5/2 x (-2/3) = -5/3 ∈ R
Isso é evidência suficiente para concluir que: A multiplicação de números reais é uma fechadura algébrica.
Esta definição pode ser estendida a todas as operações em números reais, embora possamos encontrar certas exceções.

Casos especiais em R
Divisão
Como primeiro caso especial, a divisão é observada, onde a seguinte exceção é observada:
∀ A ˄ B ∈ R → A / B ∉ R ↔ B = 0
Para todos os A e B que pertencem a R temos que A entre B não pertence aos reais se e somente se B for igual a zero.
Este caso refere-se à restrição de não poder dividir por zero. Como zero pertence aos números reais, conclui-se que: euA divisão não é um bloqueio aos reais.
Arquivamento
Existem também operações de potenciação, mais especificamente as de radicalização, onde são apresentadas exceções para potências radicais de índice par:
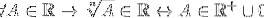
Para todo A que pertence aos reais, a enésima raiz de A pertence aos reais, se e somente se A pertencer aos reais positivos unidos a um conjunto cujo único elemento é zero.
Desta forma, denota-se que as raízes pares aplicam-se apenas a reais positivos e conclui-se que a potenciação não é um bloqueio em R.
Logaritmo
De forma homóloga, isso pode ser visto pela função logarítmica, que não é definida para valores menores ou iguais a zero. Para verificar se o logaritmo é um bloqueio de R, proceda da seguinte forma:
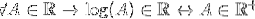
Para todo A que pertence aos reais, o logaritmo de A pertence aos reais, se e somente se A pertence aos reais positivos.
Ao excluir os valores negativos e zero que também pertencem a R, pode-se afirmar que:
O logaritmo não é um bloqueio dos números reais.
Exemplos
Verifique o bloqueio para adição e subtração de números naturais:
Soma em N
A primeira coisa é verificar a condição de bloqueio para os diferentes elementos do conjunto dado, onde se for observado que algum elemento rompe com a condição, a existência de um bloqueio pode ser negada automaticamente.
Esta propriedade é verdadeira para todos os valores possíveis de A e B, conforme observado nas seguintes operações:
1 + 3 = 4 ∈ N
5 + 7 = 12 ∈ N
1000 + 10000 = 11000 ∈ N
Não há valores naturais que quebrem a condição de bloqueio, portanto, conclui-se:
A soma é um bloqueio em N.
Subtrair em N
Eles estão procurando por elementos naturais capazes de quebrar a condição; A - B pertence aos nativos.
Operando é fácil encontrar pares de elementos naturais que não atendem à condição de bloqueio. Como por exemplo:
7 - 10 = -3 ∉ a N
Desta forma, podemos concluir que:
A subtração não é um bloqueio do conjunto de números naturais.
Exercícios propostos
1-Mostra se a propriedade de bloqueio é cumprida para o conjunto de números racionais Q, para as operações de adição, subtração, multiplicação e divisão.
2-Explique se o conjunto de números reais é uma trava do conjunto de inteiros.
3-Determine qual conjunto numérico pode ser bloqueado dos números reais.
4-Prove a propriedade de bloqueio para o conjunto de números imaginários, no que diz respeito à adição, subtração, multiplicação e divisão.
Referências
- Panorama da matemática pura: a escolha Bourbakist. Jean Dieudonné. Reverte, 1987.
- Teoria dos números algébricos. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. Universidade Nacional Autônoma do México, 1975.
- Álgebra Linear e suas Aplicações. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
- Estruturas algébricas V: teoria do corpo. Hector A. Merklen. Organização dos Estados Americanos, Secretaria-Geral, 1979.
- Introdução à álgebra comutativa. Michael Francis Atiyah, I. G. MacDonald. Reverte, 1973.

Ainda sem comentários