O proporcionalidade composta ou múltipla É a relação entre mais de duas magnitudes, onde se observa proporcionalidade direta e inversa entre os dados e o desconhecido. Esta é uma versão mais avançada da proporcionalidade simples, embora as técnicas utilizadas em ambos os procedimentos sejam semelhantes..
Por exemplo, se 7 pessoas são necessárias para descarregar 10 toneladas de mercadoria em 3 horas, a proporcionalidade composta pode ser usada para calcular quantas pessoas serão necessárias para descarregar 15 toneladas em 4 horas..
Para responder a esta questão, é conveniente fazer uma tabela de valores para estudar e relacionar as magnitudes e incógnitas..
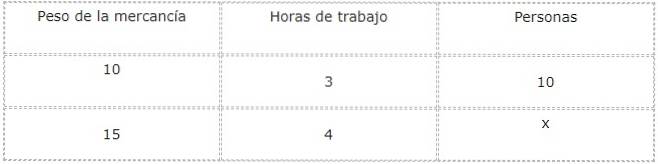
Passamos a analisar os tipos de relações entre cada magnitude e a atual incógnita, que para este caso corresponde ao número de pessoas que irão trabalhar..
Conforme o peso da mercadoria aumenta, também aumenta o número de pessoas necessárias para descarregá-la. Por isso, a relação entre peso e trabalhadores é direta.
Por outro lado, à medida que aumenta o número de trabalhadores, diminui a jornada de trabalho. Por isso, a relação entre pessoas e jornada de trabalho é do tipo inverso.
Índice do artigo
Para resolver exemplos como o acima, o método da regra de três compostos é mais usado. Consiste em estabelecer os tipos de relação entre magnitudes e incógnitas e, em seguida, representar um produto entre frações.
Com relação ao exemplo inicial, as frações correspondentes à tabela de valores estão organizadas da seguinte forma:
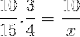
Mas antes de resolver e resolver o desconhecido, as frações correspondentes à relação inversa devem ser invertidas. Que para este caso correspondem ao tempo variável. Desta forma, a operação a ser resolvida será:
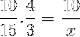
Cuja única diferença é a inversão da fração correspondente à variável de tempo 4/3. Prosseguimos para operar e limpar o valor de x.
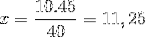
Assim, são necessárias mais de onze pessoas para poder descarregar 15 toneladas de mercadoria em 4 horas ou menos.
Proporcionalidade é a relação constante entre as grandezas sujeitas a alterações, que serão simétricas para cada uma das grandezas envolvidas. Existem relações direta e inversamente proporcionais, definindo assim os parâmetros de proporcionalidade simples ou composta..
Consiste em uma relação de proporção entre variáveis, que apresentam o mesmo comportamento quando modificadas. É muito frequente no cálculo de percentagens referentes a magnitudes diferentes de cem, onde se aprecia a sua estrutura fundamental..
A título de exemplo, pode-se calcular 15% de 63. À primeira vista, essa porcentagem não pode ser facilmente avaliada. Mas implementando a regra de três, pode-se fazer a seguinte relação: se 100% for 63, então 15%, quanto será?
100% - 63
15% -X
E a operação correspondente é:
(15%. 63) / 100% = 9,45
Onde os sinais de porcentagem são simplificados e obtém-se a figura 9,45, que representa 15% de 63.
Como o próprio nome indica, neste caso a relação entre as variáveis é oposta. A relação inversa deve ser estabelecida antes de proceder ao cálculo. Seu procedimento é homólogo ao da regra direta de três, exceto quanto ao investimento na fração a ser apurada..
Por exemplo, 3 pintores precisam de 5 horas para terminar uma parede. Em quantas horas 4 pintores o terminariam?
Nesse caso, a relação é inversa, pois à medida que aumenta o número de pintores, o tempo de trabalho deve diminuir. O relacionamento é estabelecido;
3 pintores - 5 horas
4 pintores - X horas
À medida que o relacionamento é revertido, a ordem de operação é revertida. Sendo este o caminho correto;
(3 pintores). (5 horas) / 4 pintores = 3,75 horas
O termo pintores é simplificado, e o resultado é 3,75 horas.
Para estar na presença de uma proporcionalidade composta ou múltipla, é necessário encontrar os dois tipos de relação entre as magnitudes e as variáveis.
- Direta: a variável tem o mesmo comportamento da incógnita. Ou seja, quando um aumenta ou diminui, o outro se altera igualmente.
- Inverso: a variável apresenta um comportamento antônimo ao da incógnita. A fração que define a referida variável na tabela de valores deve ser invertida, para representar a relação inversamente proporcional entre variável e desconhecida..
É muito comum confundir a ordem das magnitudes ao trabalhar com proporcionalidades compostas, ao contrário do que acontece nos cálculos de proporção usuais, cuja natureza é em grande parte direta e solucionável por meio de uma regra de três simples..
Por esse motivo, é importante examinar a ordem lógica dos resultados, verificando a coerência das figuras produzidas pela regra de três compostos..
No exemplo inicial, cometer esse erro resultaria em 20 como resultado. Ou seja, 20 pessoas para descarregar 15 toneladas de mercadoria em 4 horas.
A simple vista no parece un resultado descabellado, pero resulta curioso un aumento de casi un 200% en el personal (de 7 a 20 personas) cuando el aumento de mercancía es de un 50%, e incluso con un mayor margen de tiempo para realizar o trabalho.
Desta forma, a verificação lógica dos resultados representa uma etapa importante na implementação da regra dos três compostos..
Embora de natureza mais básica no que diz respeito ao treinamento matemático, a folga representa um passo importante nos casos de proporcionalidade. Uma folga errada é suficiente para invalidar qualquer resultado obtido na regra de três simples ou composta..
A regra de três ficou conhecida no Ocidente por meio dos árabes, com publicações de diversos autores. Entre eles Al-Jwarizmi e Al-Biruni.
Al-Biruni, graças ao seu conhecimento multicultural, teve acesso a vasta informação sobre esta prática em suas viagens à Índia, sendo responsável pela mais extensa documentação sobre a regra de três..
Ele argumenta em sua pesquisa que a Índia foi o primeiro lugar onde o uso da regra de três se tornou comum. O escritor garante que foi realizado de forma fluida nas suas versões direta, inversa e até composta..
A data exata em que a regra de três se tornou parte do conhecimento matemático da Índia ainda é desconhecida. No entanto, o documento mais antigo abordando essa prática, o manuscrito Bakhshali, foi descoberto em 1881. Ele está atualmente em Oxford.
Muitos historiadores da matemática afirmam que este manuscrito data do início da era atual..
Uma companhia aérea deve transportar 1.535 pessoas. Sabe-se que com 3 aviões demoraria 12 dias para levar o último passageiro ao destino. Mais 450 pessoas chegaram à companhia aérea e 2 aviões foram consertados para ajudar nessa tarefa. Quantos dias a companhia aérea levará para transferir o último passageiro ao seu destino?
A relação entre o número de pessoas e os dias de trabalho é direta, pois quanto maior o número de pessoas, mais dias demorará para realizar esse trabalho..
Por outro lado, a relação entre aviões e dias é inversamente proporcional. Conforme o número de aviões aumenta, os dias necessários para transferir todos os passageiros diminuem.
A tabela de valores referente a este caso é feita.
Conforme detalhado no exemplo inicial, o numerador e o denominador devem ser invertidos na fração correspondente à variável inversa em relação à incógnita. A operação é a seguinte:
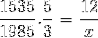
X = 71460/7675 = 9,31 dias
Para transferir 1985 pessoas usando 5 aviões, leva mais de 9 dias.
Uma safra de milho de 25 toneladas é levada para os caminhões de carga. Sabe-se que no ano anterior demorou 8 horas com uma folha de pagamento de 150 trabalhadores. Se neste ano a folha de pagamento aumentou 35%, quanto tempo demoraria para encher os caminhões de carga com uma safra de 40 toneladas??
Antes de representar a tabela de valores, deve-se definir o número de trabalhadores para este ano. Isso aumentou 35% em relação ao número inicial de 150 trabalhadores. Para isso, uma regra direta de três é usada.
100% - 150
35% - X
X = (35.100) / 100 = 52,5. Este é o número de trabalhadores adicionais em relação ao ano anterior, obtendo-se um número total de 203 trabalhadores, após arredondamento do valor obtido.
Prosseguimos para definir a tabela de dados correspondente
Para este caso, o peso representa uma variável diretamente relacionada ao tempo desconhecido. Por outro lado, a variável trabalhadores tem relação inversa com o tempo. Quanto maior for o número de trabalhadores, menor será a jornada de trabalho.
Levando essas considerações em consideração e invertendo a fração correspondente à variável workers, passamos a calcular.
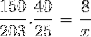
X = 40600/6000 = 6,76 horas
O dia levará pouco menos de 7 horas.
- Defina 73% de 2875.
- Calcule quantas horas Teresa dorme, caso se saiba que ela dorme apenas 7% do total do dia. Defina quantas horas você dorme por semana.
- Um jornal publica 2.000 exemplares a cada 5 horas, usando apenas 2 máquinas de impressão. Quantas cópias ele vai produzir em 1 hora, se usar 7 máquinas? Quanto tempo levará 10.000 cópias usando 4 máquinas?
Ainda sem comentários