
Características da projeção de Mercator, usos, vantagens e desvantagens
O Projeção mercator é um sistema para representar graficamente a superfície da Terra em um plano, a fim de fazer mapas. Entre as quase 400 projeções cartográficas existentes, a de Mercator é uma espécie de projeção cilíndrica..
Gerardus Mercator, em 1569, imaginou a Terra dentro de um cilindro cujo diâmetro era igual ao equador terrestre. Então, ele estava projetando linhas do centro da Terra até o cilindro. Assim, estava representando todos os pontos do contorno da superfície terrestre, que quando unidos representam as linhas das formas geográficas..
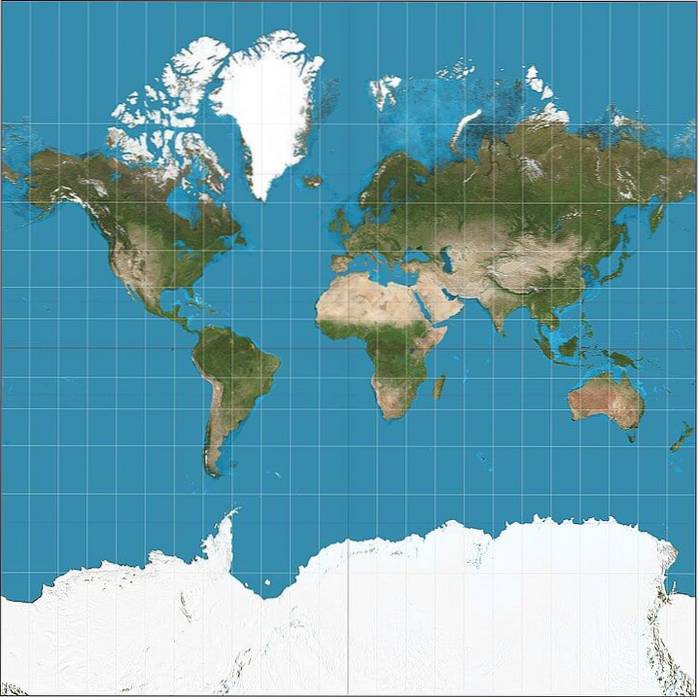
Os mapas obtidos por esta projeção são especialmente úteis para cartas de navegação, pois permitem traçar rotas em linha reta..
Sua principal vantagem é que representa muito bem as formas geográficas, mantendo os ângulos reais. No entanto, ele altera as proporções das áreas de terra à medida que nos afastamos do equador..
Índice do artigo
- 1 Características da projeção de Mercator
- 1.1 Projeções do mapa
- 1.2 Projeção cilíndrica
- 1.3 Orientação do mapa
- 2 usos
- 2.1 Navegação
- 2.2 Objetivos escolares
- 2.3 Sistemas de posicionamento geográfico na WEB
- 3 vantagens
- 4 desvantagens
- 4.1 Os pólos geográficos
- 5 referências
Características da projeção Mercator
Projeções de mapa
A Terra tem uma forma semelhante à de uma elipse circular (geóide, com pólos achatados e um equador saliente). Nesta superfície curva estão os contornos dos continentes e ilhas.
Isso implica uma dificuldade ao tentar representar essa superfície curva em um plano e para isso os geógrafos usam as projeções. No entanto, todas as projeções geram alguma deformação ou distorção em relação à realidade e nenhum método representa com precisão a superfície terrestre real.
Portanto, existem diferentes tipos de projeções cartográficas, cada uma com vantagens e desvantagens que podem ser planas, cônicas, cilíndricas ou poliédricas, entre outras. Neste caso, a projeção de Mercator é uma projeção cilíndrica.
Projeção cilíndrica
Para resolver o problema de projetar a superfície da Terra no plano, Mercator imaginou a Terra dentro de um cilindro do mesmo diâmetro. Onde o eixo principal ou longitudinal do referido cilindro coincidiu com o eixo de rotação da Terra (projeção cilíndrica normal).
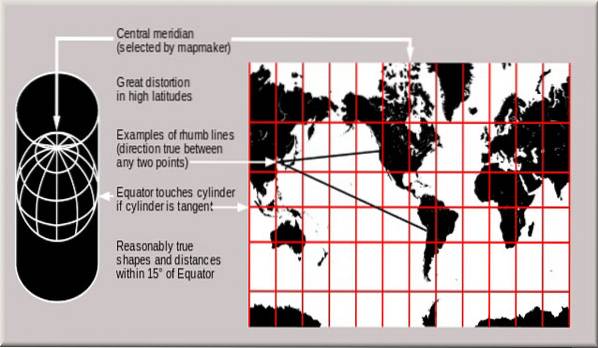
Posteriormente, foi projetando linhas imaginárias desde o centro do planeta passando por cada ponto do contorno da superfície terrestre até interceptar o cilindro. Assim, ele estava projetando cada ponto do mapa no cilindro e estendendo-o como um plano e juntando os pontos, ele obteve uma imagem bastante exata do contorno da Terra.
Neste caso é uma projeção cilíndrica normal conformada, onde as formas e ângulos são mantidos. Como as distâncias, mas não as proporções relativas das superfícies no plano.
Orientação do mapa
O mapa construído por meio da projeção de Mercator também se caracteriza por ser orientado com o norte para cima e com a Europa ocupando o centro. Embora isso pareça óbvio devido ao uso extensivo que é feito deste mapa, a realidade é que mapas igualmente válidos podem ser feitos de diferentes perspectivas.
Formulários
Navegação
Este tipo de projeção de mapa foi projetado por Mercator para criar cartas de navegação (mapas destinados ao uso por marítimos). Desde então tem sido utilizado para este fim, dada a sua facilidade de traçar percursos de curso constantes através de linhas rectas..
Fins escolares
Por outro lado, seu uso se generalizou, pois é usado como uma representação real da Terra em outras áreas. É assim que o encontramos nos livros didáticos, nos mapas das paredes das escolas e em muitos outros contextos..
No entanto, foi apontado que os mapas construídos usando a projeção de Mercator não devem ser usados para a educação escolar. Isso se deve ao fato de que a relação das superfícies entre os continentes é deformada.
Assim, os continentes com maior massa de terra ao redor do equador, mantêm uma superfície relativa no mapa semelhante à real. No entanto, os continentes localizados ao norte do equador são maiores do que o real..
A projeção Gall-Peters de 1885, que é uma projeção cilíndrica normal equidistante, foi proposta para uso escolar. Salva as proporções da superfície, restringindo a projeção de Mercator para cartas de navegação, onde suas características o tornam eficiente..
Sistemas de posicionamento geográfico na WEB
Sistemas de geolocalização online através da INTERNET, como Mapas do Google, use a projeção de Mercator. Especificamente, a chamada Projeção Web Mercator ou Web do Google Mercator, que o Google adotou em 2005 e se espalhou entre os provedores de mapas online.
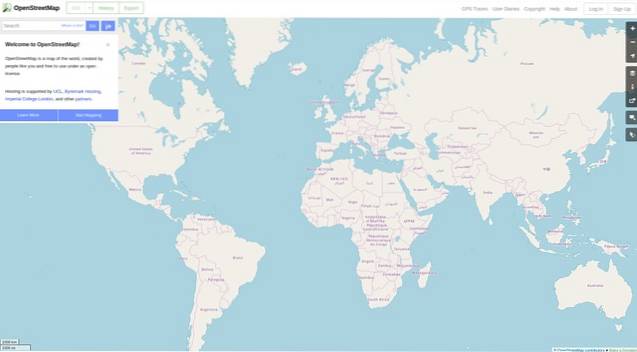
Isso se deve principalmente ao fato de que os cálculos matemáticos necessários para sua execução são mais simples do que os de outros tipos de projeções. Bem como o fato de nesta projeção os ângulos serem mantidos como realmente são.
Vantagem
O mapa de projeção Mercator é ideal para traçar rotas em linha reta para navegação e inclui uma fórmula geométrica para corrigir distorções, transformando medições em graus de latitude. Por outro lado, esta projeção do mapa mantém os ângulos entre os pontos como realmente são..
Além disso, como já indicado, a projeção de Mercator tem a grande vantagem da menor complexidade das operações matemáticas necessárias para sua realização..
Desvantagens
A desvantagem fundamental da projeção de Mercator para mapas tem a ver com as proporções dos tamanhos das massas de terra. Perto do equador as proporções são mantidas, mas ao se afastar do equador as áreas aumentam em relação à realidade.
Isso porque a projeção foi feita em um cilindro, onde apenas o equador é tangente a ele, sem compensar a deformação gerada. Os pontos na altura do equador são paralelos ao cilindro, enquanto os pontos distantes dele não são..
Neste último, as linhas que os projetam cruzam o cilindro em pontos diagonais e mais afastados uns dos outros. Portanto, os paralelos e meridianos do sistema de referência ou coordenadas são estendidos para o norte e para o sul..

Isso tem como consequência que ao observar um mapa feito com a projeção de Mercator, vemos, por exemplo, o Alasca maior que o Brasil. Porém, a realidade é que o Brasil é 5 vezes maior que o Alasca.
Assim como também dá a impressão de que a Península Ibérica tem quase o mesmo tamanho da Venezuela ou da Colômbia, quando são maiores. Da mesma forma, a Rússia no mapa de Mercator é vista 7 vezes maior que a Austrália, quando possui apenas uma área duas vezes maior que este continente..
Os pólos geográficos
Outra deficiência da projeção de Mercator é que no mapa gerado, tanto o pólo norte quanto o pólo sul estão fora da área. Isso é particularmente problemático para o Pólo Sul, onde o continente da Antártica está localizado..
Referências
- Fernández-Coppel, I.A. (s (f). Projeção UTM (Universal Transversa Mercator). Localizações geográficas. Escola Técnica Superior de Engenharia Agrária. Universidade de Valladolid.
- Gómez-Moreno, R.A. (2004). Guia de projeções do mapa. Instituto Nacional de Estatística. Geografia e Informática. México.
- Miraglia, M., Flores, A.P., Rivarola e Benitez, M., D'Liberis, M., Galván, L., Natale, D. e Rodríguez, M. (2010). Manual de Cartografia, Sensoriamento Remoto e Sistemas de Informação Geográfica. Laboratório de Sistemas de Informação Geográfica. Instituto del Conurbano. Universidade Nacional do General Sarmiento.
- Raisz, E. e Mantero, J.M. (2005). Cartografia geral. Trad. 7ª edição Omega, Barcelona.
- Robinson, A.H., Sale, R.D., Morrison, J.L., Muehrcke, P.C., Ravella-Vives, J.M., Ferrer, R.M. (1987). Elementos de mapeamento. Omega 1ª Edição.



Ainda sem comentários