Óptica geométrica o que estuda, leis, aplicações, exercícios

O ótica geométrica é o ramo da Física que se concentra em estudar a maneira como a luz se espalha e é refletida ao passar de um meio para outro, sem levar em conta os efeitos da difração..

Desta forma, a luz é representada geometricamente por raios, linhas imaginárias perpendiculares às frentes das ondas de luz..

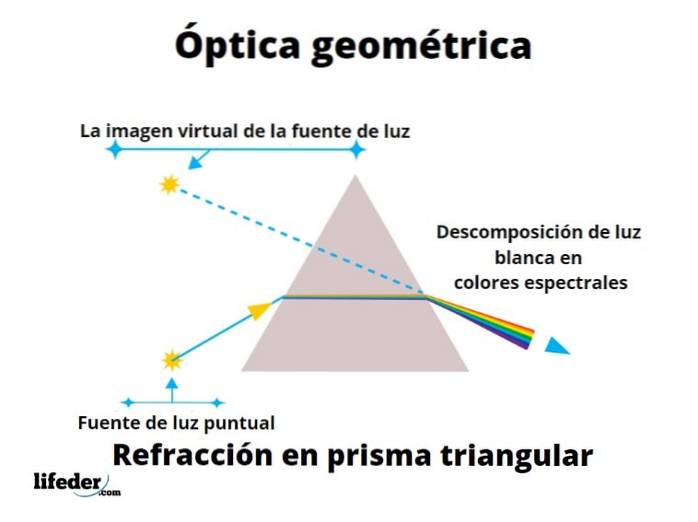
Raios de luz emergem de fontes de luz como o Sol, uma chama ou uma lâmpada, espalhando-se em todas as direções. As superfícies refletem parcialmente esses raios de luz e é por isso que podemos vê-los, graças ao fato de que os olhos contêm elementos sensíveis à luz..

Graças ao tratamento de raios, a ótica geométrica não leva tanto em conta os aspectos ondulatórios da luz, mas explica como as imagens se formam nos olhos, nos espelhos e nos projetores, onde o fazem e como aparecem..

Os princípios fundamentais da óptica geométrica são a reflexão e a refração da luz. Os raios de luz atingem certos ângulos nas superfícies que se encontram e, graças a isso, uma geometria simples ajuda a manter o controle de sua trajetória em cada meio.

Isso explica coisas do dia a dia, como olhar nossa imagem no espelho do banheiro, ver uma colher de chá que parece entortar dentro de um copo cheio d'água ou melhorar a visão com óculos adequados..

Precisamos de luz para nos relacionarmos com o meio ambiente, por isso seu comportamento sempre surpreendeu os observadores, que se questionaram sobre sua natureza..

Índice do artigo

• 1 O que a óptica geométrica estuda? (Objeto de estudo)
• 2 Conceitos básicos em óptica geométrica
  • 2.1 Índice de refração
  • 2.2 Caminho óptico
• 3 leis da ótica geométrica
  • 3.1 Princípio de Fermat
  • 3.2 Lei da reflexão
  • 3.3 Lei de Snell
• 4 aplicativos
  • 4.1 Espelhos e lentes
  • 4.2 Instrumentos ópticos
  • 4.3 Fibra ótica
• 5 Exercício resolvido
  • 5.1 Solução
• 6 referências

O que a óptica geométrica estuda? (Objeto de estudo)

A óptica geométrica estuda a propagação da luz no vácuo e em vários meios, sem explicar em que consiste a sua verdadeira natureza. Para isso faz uso do modelo de raio e geometria simples.

Um raio é o caminho que a luz segue em um determinado meio transparente, o que é uma excelente aproximação, desde que o comprimento de onda seja pequeno em comparação com o tamanho dos objetos..

Isso é verdade em muitos casos do dia a dia, como os mencionados no início..

Existem duas premissas fundamentais da óptica geométrica:

-A luz se propaga de forma retilínea.

-Ao se propagar por diversos meios, a luz o faz seguindo leis empíricas, ou seja, obtida por meio de experimentação..

Conceitos básicos em óptica geométrica

Índice de refração

A velocidade da luz em um meio material é diferente da velocidade do vácuo. Lá sabemos que é 300.000 km / s, mas no ar é um pouco menor, e ainda mais na água ou no vidro..

O índice de refração é uma quantidade adimensional, que é definida como o quociente entre a velocidade com que a luz viaja no vácuo c_ou e velocidade c  no referido meio:

n = c_ou / c

Caminho ótico

É o produto entre a distância percorrida pela luz para passar de um ponto a outro, e o índice de refração do meio:

L = s. n

Onde L é o caminho óptico, s é a distância entre os dois pontos e n representa o índice de refração, assumindo constante.

Por meio do caminho óptico, os raios de luz que se movem em diferentes meios são comparados.

Ângulo de incidência

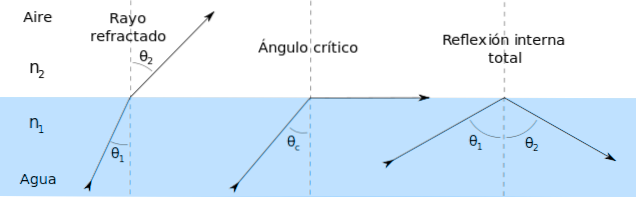
É o ângulo que o raio de luz forma com a linha normal para uma superfície que separa dois meios.

Leis da Óptica Geométrica

Princípio de Fermat

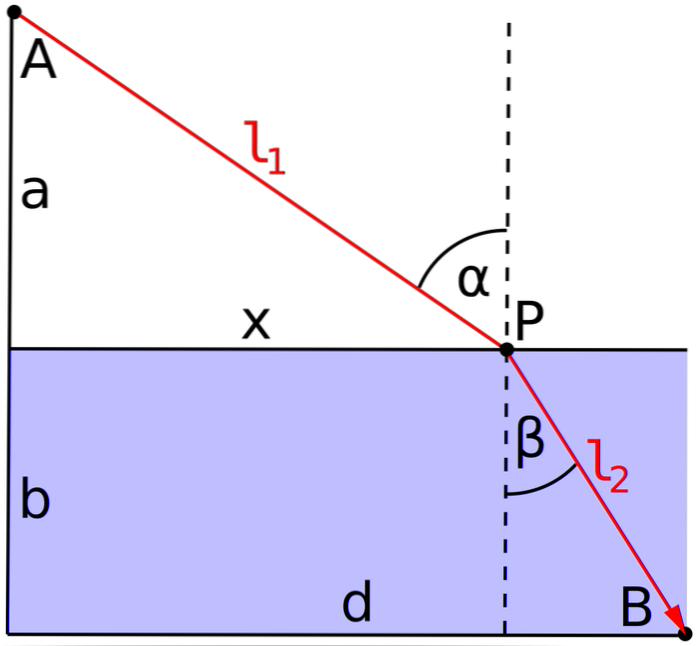
O matemático francês Pierre de Fermat (1601-1665) observou que:

Quando um raio de luz viaja entre dois pontos, ele segue o caminho em que leva o tempo mínimo.

E uma vez que a luz se move com velocidade constante, seu caminho deve ser retilíneo.

Em outras palavras, o princípio de Fermat afirma que o caminho do raio de luz é tal que o caminho óptico entre dois pontos é mínimo..

Lei da reflexão

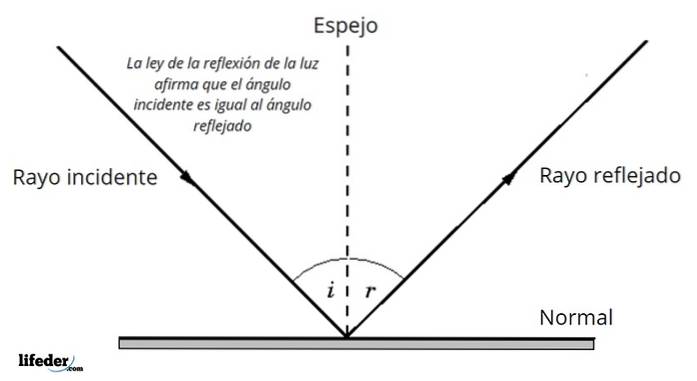
Ao atingir a superfície que separa dois meios diferentes, uma parte do raio incidente - ou todo ele - é refletido de volta e o faz com o mesmo ângulo medido em relação à normal à superfície com a qual atingiu..

Em outras palavras, o ângulo de incidência é igual ao ângulo de reflexão:

 θ_eu = θ_{eu '}

Lei de Snell

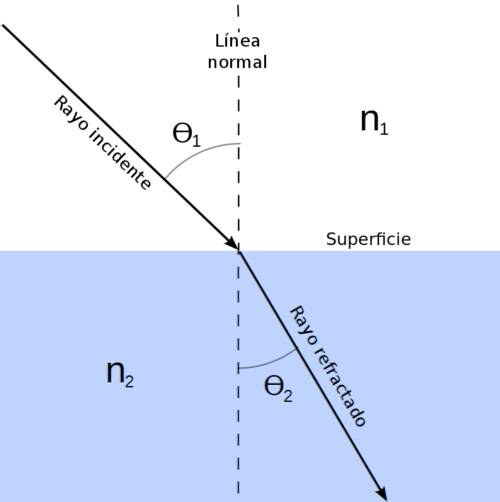
O matemático holandês Willebrord Snell (1580-1626) observou cuidadosamente o comportamento da luz ao passar do ar para a água e o vidro.

Ele viu que quando um raio de luz incide na superfície que separa dois meios, formando um certo ângulo com ele, uma parte do raio é refletida de volta para o primeiro meio e a outra continua seu caminho através do segundo..

Assim, ele deduziu a seguinte relação entre as duas mídias:

n_{1 ⋅} sen θ₁ = n_{2 ⋅} sen θ_dois

Onde₁ e n_dois são os respectivos índices de refração, enquanto que θ₁ Y  θ_dois  são os ângulos de incidência e refração, medidos em relação ao normal à superfície, conforme figura acima.

Formulários

Espelhos e lentes

Os espelhos são superfícies altamente polidas que refletem a luz dos objetos, permitindo a formação de imagens. Espelhos planos, como os do banheiro ou carregados na bolsa, são comuns.

Uma lente consiste em um dispositivo óptico com duas superfícies refrativas muito próximas. Quando um feixe de raios paralelos passa por uma lente convergente, eles convergem em um ponto, formando uma imagem. Quando se trata de lentes divergentes, acontece o oposto: os raios do feixe divergem em um ponto.

As lentes são freqüentemente usadas para corrigir erros de refração no olho, bem como em vários instrumentos de aumento ótico..

Instrumentos ópticos

Existem instrumentos ópticos que permitem a ampliação de imagens, por exemplo microscópios, lupas e telescópios. Existem também aqueles para olhar acima do nível dos olhos, como periscópios.

As câmeras fotográficas são utilizadas para capturar e preservar as imagens, as quais contêm um sistema de lentes e um elemento de gravação para salvar a imagem formada..

Fibra ótica

É um material comprido, fino e transparente à base de sílica ou plástico, utilizado para transmissão de dados. Aproveita a propriedade de reflexão total: quando a luz atinge o meio em determinado ângulo, não ocorre refração, portanto o raio pode percorrer longas distâncias, saltando dentro do filamento.

Exercício resolvido

Os objetos no fundo de uma piscina ou lagoa parecem estar mais próximos do que realmente estão, o que se deve à refração. Em que profundidade aparente um observador vê uma moeda que está no fundo de um poço de 4 m de profundidade??

Suponha que o raio que emerge da moeda atinja o olho do observador em um ângulo de 40º em relação ao normal..

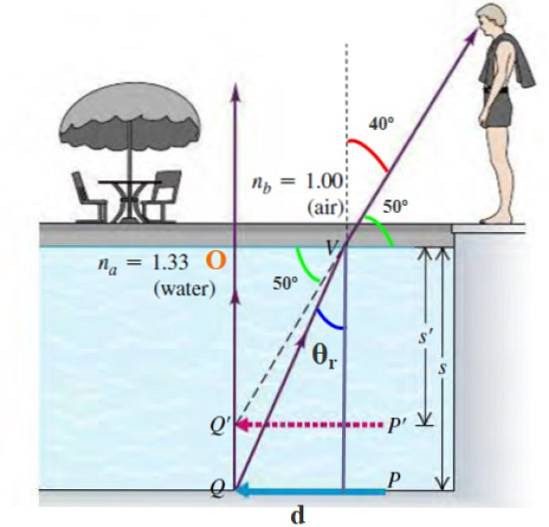
Fato: o índice de refração da água é 1,33, o do ar é 1.

Solução

A profundidade aparente da moeda é s 'e a profundidade da piscina é s = 4 m. A moeda está no ponto Q e o observador a vê no ponto Q '. A profundidade deste ponto é:

s '= s - Q'Q

Da lei de Snell:

n_b ⋅ sin 40º = n_para ⋅ sen θ_r

sen θ_r = (n_b ⋅ sin 40º) ÷ n_para = sin 40º / 1,33 = 0,4833

θ_r = arcsen (0,4833) = 28,9º

Conhecendo este ângulo, calculamos a distância d = OV do triângulo retângulo, cujo ângulo agudo é θ_r:

tan 28,9º = OV / 4 m

OV = 4m × tan 28,9º = 2,154 m

Por outro lado:

tan 50º = OQ '/ OV

Portanto:

OQ '= OV × tan 50º = 2,154 m × tan 50º = 2,57 m.

Referências

1. Bauer, W. 2011. Physics for Engineering and Sciences. Volume 2. Mc Graw Hill.
2. Figueras, M. Óptica geométrica: óptica sem ondas. Universidade Aberta da Catalunha.
3. Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed Prentice Hall.
4. Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 2. 7º. Ed. Cengage Learning.
5. Tippens, P. 2011. Physics: Concepts and Applications. 7ª Edição. Colina Mcgraw.