
Qual é o equilíbrio da partícula? (Com exemplos)
O equilíbrio de partículas É um estado em que uma partícula é encontrada quando as forças externas que atuam sobre ela são mutuamente canceladas. Isso pressupõe que mantenha um estado constante, de forma que pode ocorrer de duas maneiras diferentes dependendo da situação específica.
O primeiro é estar em equilíbrio estático, no qual a partícula é imóvel; e o segundo é o equilíbrio dinâmico, onde a soma das forças se cancela, mas, no entanto, a partícula tem movimento retilíneo uniforme.

O modelo de partículas é uma aproximação muito útil para estudar o movimento de um corpo. Consiste em assumir que toda a massa do corpo está concentrada em um único ponto, independentemente do tamanho do objeto. Desta forma, você pode representar um planeta, um carro, um elétron ou uma bola de bilhar.
Índice do artigo
- 1 A força resultante
- 2 diagramas de corpo livre
- 3 maneiras de aplicar a condição de equilíbrio
- 3.1 Duas forças de igual magnitude e direção e direções opostas
- 3.2 Duas forças de magnitude diferente, mesma direção e direções opostas
- 3.3 Duas forças de igual magnitude e direção diferente
- 3.4 Três forças com diferentes direções
- 4 fricção
- 4.1 O atrito dinâmico
- 5 exemplo trabalhado
- 5.1 Solução
- 6 referências
A força resultante
O ponto que representa o objeto é onde atuam as forças que o afetam. Todas essas forças podem ser substituídas por uma única que faz o mesmo efeito, que é chamada força resultante ou força resultante e é denotado como FR ou FN.
De acordo com a segunda lei de Newton, quando há uma força resultante desequilibrada, o corpo experimenta uma aceleração proporcional à força:
FR = m.a
Onde para é a aceleração que o objeto adquire graças à ação da força e m é a massa do objeto. O que acontece se o corpo não for acelerado? Exatamente o que foi indicado no início: o corpo está em repouso ou se move com movimento retilíneo uniforme, ao qual falta aceleração.
Para uma partícula em equilíbrio, é válido garantir que:
FR = 0
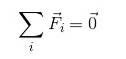
Visto que adicionar vetores não implica necessariamente adicionar os módulos, os vetores devem ser decompostos. Assim, é válido expressar:
Fx = m.ax = 0; FY = m.aY = 0; Fz = m.az = 0
Diagramas de corpo livre
Para visualizar as forças que atuam sobre a partícula, é conveniente fazer um diagrama de corpo livre, no qual todas as forças que atuam sobre o objeto são representadas por setas..
As equações acima são de natureza vetorial. Ao decompor as forças, elas se distinguem por signos. Desta forma, é possível que a soma de seus componentes seja zero.
A seguir estão orientações importantes para tornar o desenho útil:
- Escolha um sistema de referência no qual a maior quantidade de forças estão localizadas nos eixos de coordenadas.
- O peso é sempre desenhado verticalmente para baixo.
- No caso de duas ou mais superfícies em contato, existem forças normais, que são sempre atraídas empurrando o corpo e perpendiculares à superfície que o exerce..
- Para uma partícula em equilíbrio pode haver fricções paralelas à superfície de contato e opostas ao possível movimento, se a partícula for considerada em repouso, ou definitivamente em oposição, se a partícula se mover com MRU (movimento retilíneo uniforme).
- Se houver uma corda, a tensão é sempre puxada ao longo dela e puxando o corpo.
Maneiras de aplicar a condição de equilíbrio
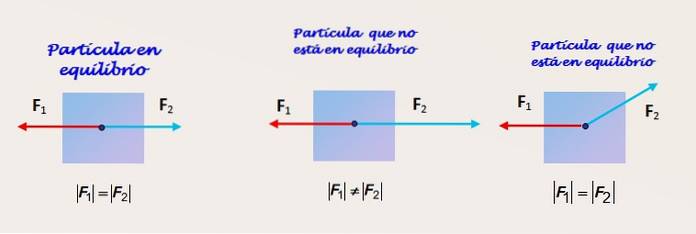
Duas forças de igual magnitude e direção e direções opostas
A Figura 2 mostra uma partícula na qual duas forças atuam. Na figura à esquerda a partícula recebe a ação de duas forças F1 e Fdois que têm a mesma magnitude e atuam na mesma direção e em direções opostas.
A partícula está em equilíbrio, mas mesmo assim com as informações fornecidas não é possível saber se o equilíbrio é estático ou dinâmico. São necessárias mais informações sobre o quadro de referência inercial a partir do qual o objeto é observado.
Duas forças de magnitude diferente, a mesma direção e direções opostas
A figura ao centro mostra a mesma partícula, que desta vez não está em equilíbrio, pois a magnitude da força Fdois é maior do que F1. Portanto, há uma força desequilibrada e o objeto tem uma aceleração na mesma direção de Fdois.
Duas forças de igual magnitude e direção diferente
Finalmente, na figura da direita vemos um corpo que também não está em equilíbrio. Apesar do fato de que F1 e Fdois têm igual magnitude, a força Fdois não está na mesma direção que 1. O componente vertical de Fdois não é neutralizado por nenhum outro e a partícula experimenta uma aceleração nessa direção.
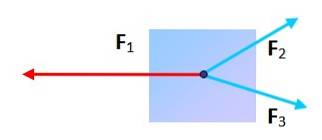
Três forças com direções diferentes
Uma partícula sujeita a três forças pode estar em equilíbrio? Sim, desde que ao colocar a ponta e a ponta de cada uma, a figura resultante seja um triângulo. Neste caso, a soma do vetor é zero.
Atrito
Uma força que freqüentemente intervém no equilíbrio da partícula é o atrito estático. É devido à interação do objeto representado pela partícula com a superfície de outra. Por exemplo, um livro em equilíbrio estático em uma mesa inclinada é modelado como uma partícula e tem um diagrama de corpo livre como o seguinte:
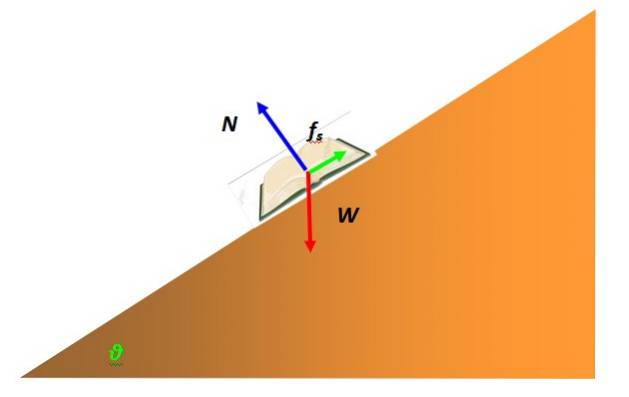
A força que impede o livro de deslizar pela superfície do plano inclinado e permanecer em repouso é o atrito estático. Depende da natureza das superfícies em contato, que microscopicamente apresentam rugosidade com picos que se entrelaçam, dificultando o movimento..
O valor máximo de atrito estático é proporcional à força normal, a força exercida pela superfície sobre o objeto apoiado, mas perpendicular a essa superfície. No exemplo do livro, é indicado em azul. Matematicamente, é expresso assim:
Fs mais∝ N
A constante de proporcionalidade é o coeficiente de atrito estático μs, que é determinado experimentalmente, é adimensional e depende da natureza das superfícies em contato.
Fs max = µs N
O atrito dinâmico
Se uma partícula está em equilíbrio dinâmico, o movimento já ocorre e o atrito estático não intervém mais. Se estiver presente alguma força de atrito que se oponha ao movimento, atua o atrito dinâmico, cuja magnitude é constante e é dada por:
Fk = µk N
Onde µk é o coeficiente de atrito dinâmico, Também depende do tipo de superfície em contato. Como o coeficiente de atrito estático, é adimensional e seu valor é determinado experimentalmente.
O valor do coeficiente de atrito dinâmico é geralmente menor do que o do atrito estático.
Exemplo trabalhado
O livro da Figura 3 está em repouso e tem massa de 1,30 kg. O avião tem um ângulo de inclinação de 30º. Encontre o coeficiente de atrito estático entre o livro e a superfície plana.
Solução
É importante selecionar um sistema de referência adequado, consulte a seguinte figura:
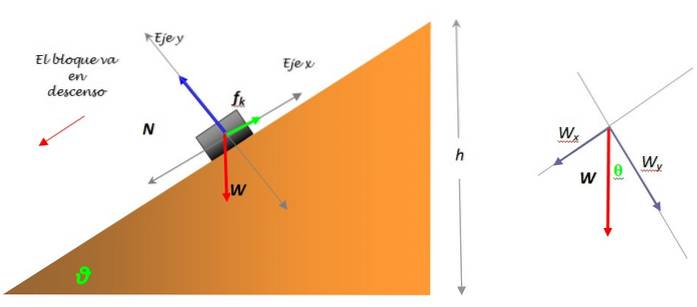
O peso do livro tem magnitude W = mg, no entanto, é necessário dividi-lo em dois componentes: Cx Y CY, uma vez que é a única força que não cai logo acima de qualquer um dos eixos coordenados. A decomposição do peso é observada na figura à esquerda.
CY = mg.cosθ = 1,30 x 9,8 x cos 30º N = 11,03 N
Cx = mg sinθ = 1,30 x 9,8 x sin 30º = 6,37 N
O segundo. A lei de Newton para o eixo vertical é:
N - Wy = 0
N = mg. cos θ = 11,03 N.
Aplicando o 2º. Lei de Newton para o eixo x, escolhendo a direção do movimento possível como positiva:
Cx - Fs = 0
O atrito máximo é Fs max= µsN, portanto:
Cx - µsN = 0
µs = Wx / N = 6,37 / 11,03 = 0,58
Referências
- Rex, A. 2011. Fundamentals of Physics. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 1. 7mãe. Ed. Cengage Learning. 120 - 124.
- Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9n / D Ed. Cengage Learning. 99-112.
- Tippens, P. 2011. Physics: Concepts and Applications. 7ª Edição. MacGraw Hill. 71-87.
- Walker, J. 2010. Physics. Addison Wesley. 148-164.



Ainda sem comentários