Qual é o módulo de cisalhamento, rigidez ou cisalhamento? (Exercícios resolvidos)

O módulo de corte descreve a resposta de um material à aplicação de uma tensão de cisalhamento que o deforma. Outros nomes freqüentemente usados ​​para o módulo de cisalhamento são módulo de cisalhamento, módulo de cisalhamento, elasticidade transversal ou elasticidade tangencial..

Quando as tensões são pequenas, as deformações são proporcionais a elas, segundo a lei de Hooke, sendo o módulo de cisalhamento a constante de proporcionalidade. Portanto:

Módulo de cisalhamento = tensão de cisalhamento / deformação

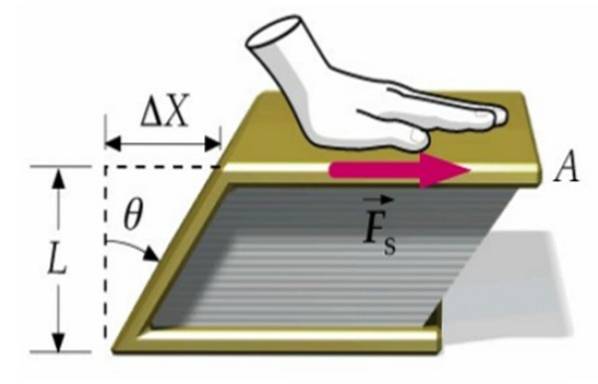
Suponha que uma força seja aplicada à capa de um livro, a outra sendo fixada na superfície da mesa. Desta forma, o livro como um todo não se move, mas se deforma quando a capa superior se move em relação à inferior na quantidade Δx.

O livro passa de uma seção transversal retangular para uma seção em forma de paralelogramo, como vemos na imagem acima.

Ser:

τ = F / A

A tensão de cisalhamento ou tensão, sendo F a magnitude da força aplicada e PARA a área em que atua.

A deformação causada é dada pelo quociente:

δ = Δx / L

Portanto, o módulo de cisalhamento, que denotaremos como G, é:

E como Δx / L não tem dimensões, as unidades de G são iguais à tensão de cisalhamento, que é a razão entre a força e a área..

No Sistema Internacional de Unidades, essas unidades são Newton / metro quadrado ou pascal, abreviado Pa. E em unidades anglo-saxônicas é libra / polegada quadrada, abreviado psi.

Índice do artigo

• 1 Módulo de corte para vários materiais
  • 1.1 Medição experimental do módulo de cisalhamento
  • 1.2 Como encontrar G?
• 2 exercícios com solução
  • 2.1 - Exercício 1
  • 2.2 - Exercício 2
• 3 referências

Módulo de corte para vários materiais

Sob a ação de forças de cisalhamento como as descritas, os objetos oferecem uma resistência semelhante à do livro, em que as camadas internas deslizam. Esse tipo de deformação só pode ocorrer em corpos sólidos, que possuem rigidez suficiente para resistir à deformação..

Por outro lado, os líquidos não oferecem este tipo de resistência, mas podem sofrer deformações volumétricas..

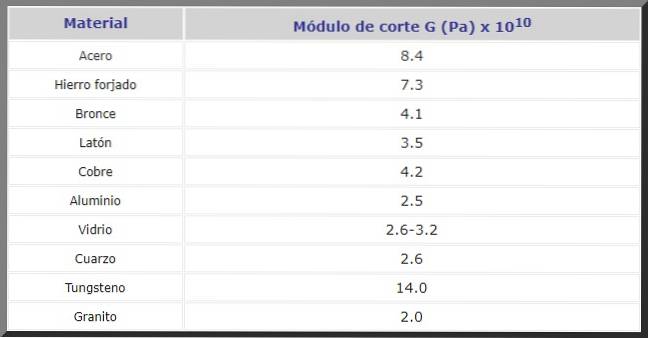
Abaixo está o módulo de corte G in Pa para vários materiais frequentemente usados ​​na construção e na fabricação de máquinas e peças de reposição de todos os tipos:

Medição experimental do módulo de cisalhamento

Para encontrar o valor do módulo de cisalhamento, amostras de cada material devem ser testadas e sua resposta à aplicação de uma tensão de cisalhamento examinada..

A amostra é uma haste feita do material, com raio R e comprimento eu conhecido, que é fixado em uma extremidade, enquanto a outra está conectada ao eixo de uma polia livre para girar.

A polia é amarrada com uma corda, na extremidade livre da qual está pendurado um peso que exerce uma força F na haste através da corda. E esta força, por sua vez, produz um momento M na haste, que então gira um pequeno ângulo θ.

Um diagrama da montagem pode ser visto na figura a seguir:

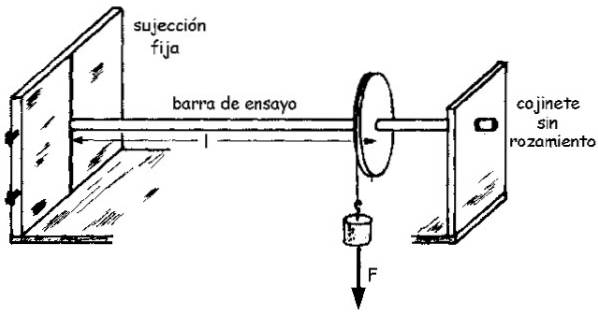
A magnitude do momento M, que denotamos como M (sem negrito) está relacionado ao ângulo girado θ através do módulo de cisalhamento G de acordo com a seguinte equação (deduzida por uma integral simples):

Como a magnitude do momento é igual ao produto do módulo da força F e o raio da polia R_p:

M = F.R_p

E a força é o peso que paira C, então:

M = W.R_p

Substituindo na equação a magnitude do momento:

Existe a relação entre peso e ângulo:

Como encontrar G?

Esta relação entre as variáveis C Y θ é linear, então os diferentes ângulos produzidos pendurando diferentes pesos são medidos.

Os pares de peso e ângulo são plotados em papel milimetrado, a melhor linha que passa pelos pontos experimentais é ajustada e a inclinação é calculada. m da dita linha.

Exercícios com solução

- Exercício 1

Uma haste de 2,5 metros de comprimento e 4,5 mm de raio é fixada em uma extremidade. A outra é conectada a uma polia de raio de 75 cm que tem um peso suspenso W de 1,3 kg. O ângulo girado é 9,5º.

Com esses dados, é necessário calcular o módulo de cisalhamento G da barra.

Solução

Da equação:

G está apagado:

E os valores indicados no enunciado são substituídos, tendo o cuidado de expressar todos os dados do Sistema Internacional de Unidades SI:

R = 4,5 mm = 4,5 x 10 ^-3 m

R_p = 75 cm = 0,075

Para ir de quilogramas (que na verdade são quilogramas - força) a newtons, multiplique por 9,8:

W = 1,3 kg-força = 1,3 x 9,8 N = 12,74 N

E, finalmente, os graus devem ser em radianos:

9,5 º = 9,5 x2π / 360 radianos = 0,1658 radianos.

Com tudo isso você tem:

= 2.237 x 10¹⁰ Pa

- Exercício 2

Um cubo feito de gel tem um lado de 30 cm. Uma de suas faces é fixa, mas ao mesmo tempo, uma força paralela de 1 N é aplicada na face oposta, que graças a ela se move 1 cm (veja o exemplo do livro na figura 1).

É necessário calcular com estes dados:

a) A magnitude da tensão de cisalhamento

b) Cepa δ

c) O valor do módulo de cisalhamento

Solução para

A magnitude da tensão de cisalhamento é:

τ = F / A

Com:

Lado A =^dois = (30 x 10^-dois cm)^dois = 0,09 m^dois

Portanto:

τ = 1 N / 0,09 m^dois = 11,1 Pa

Solução b

A deformação não é outro senão o valor de δ, dado por:

δ = Δx / L

O deslocamento da face submetida à força é de 1 cm, então:

δ = 1/30 = 0,0333

Solução c

O módulo de cisalhamento é o quociente entre a tensão de cisalhamento e a deformação:

G = Tensão de cisalhamento / deformação

Portanto:

G = 11,1 Pa / 0,033 = 336,4 Pa

Referências

1. Beer, F. 2010. Mecânica dos materiais. McGraw Hill. 5 ª. Edição.
2. Franco García, A. Solid Rigid. Medição do módulo de cisalhamento. Recuperado de: sc.ehu.es.
3. Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed Prentice Hall.
4. Resnick, R. (1999). Fisica. Vol. 1. 3ª Ed. Em espanhol. Compañía Editorial Continental S.A. por C.V.
5. Universidade de Valladolid. Departamento de Física da Matéria Condensada. Seleção de problemas. Recuperado de: www4.uva.es.