O que é impedância acústica? Aplicações e exercícios

O impedância acústica ou impedância acústica específica é a resistência do meio material à passagem das ondas sonoras. É constante para um determinado meio, que vai desde uma camada rochosa no interior da Terra até o tecido biológico.

Denotando a impedância acústica como Z, na forma matemática temos:

Z = ρ.v

Onde ρ é a densidade ev a velocidade do som do meio. Esta expressão é válida para uma onda plana se movendo em um fluido.

Em unidades do Sistema Internacional SI, a densidade é em kg / m³ e a velocidade em m / s. Portanto, as unidades de impedância acústica são kg / m^dois.s.

Da mesma forma, a impedância acústica é definida como o quociente entre a pressão pe a velocidade:

Z = p / v

Expresso desta forma, Z é análogo à resistência elétrica R = V / I, onde a pressão desempenha o papel da tensão e a velocidade da corrente. Outras unidades SI de Z seriam Pa.s / m ou N.s / m³, completamente equivalente aos dados anteriormente.

Índice do artigo

• 1 Transmissão e reflexão da onda sonora
  • 1.1 Coeficientes de transmissão e reflexão
• 2 aplicações e exercícios
  • 2.1 - Exercício resolvido 1
  • 2.2 - Exercício resolvido 2
• 3 referências

Transmissão e reflexão de ondas sonoras

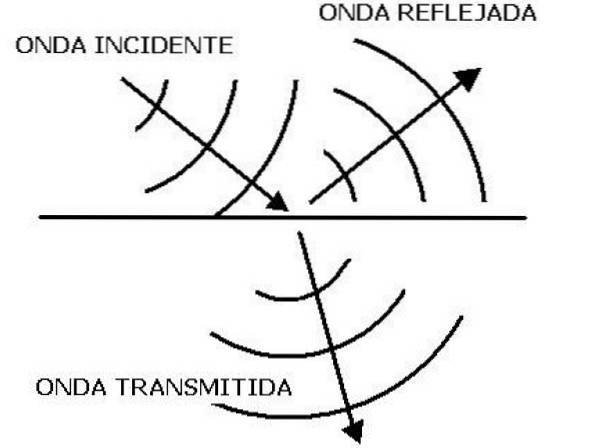
Quando você tem dois meios de impedâncias Z diferentes₁ e Z_dois, parte de uma onda sonora que atinge a interface de ambos pode ser transmitida e outra parte pode ser refletida. Essa onda refletida, ou eco, é aquela que contém informações importantes sobre o segundo meio..

A forma como a energia transportada pela onda é distribuída depende dos coeficientes de reflexão R e do coeficiente de transmissão T, duas grandezas muito úteis para estudar a propagação da onda sonora. Para o coeficiente de reflexão, é o quociente:

R = I_r / EU_ou

Onde eu_ou é a intensidade da onda incidente e eu_r é a intensidade da onda refletida. Da mesma forma, temos o coeficiente de transmissão:

T = I_t / EU_ou

Agora, pode ser mostrado que a intensidade de uma onda plana é proporcional à sua amplitude A:

I = (1/2) Z.ω^dois .PARA^dois

Onde Z é a impedância acústica do meio e ω é a frequência da onda. Por outro lado, o quociente entre a amplitude transmitida e a amplitude incidente é:

PARA_t/PARA_ou = 2Z₁/ (Z₁ +Z_dois)

O que permite o quociente I_t / EU_ou  é expresso em termos das amplitudes das ondas incidentes e transmitidas como:

eu_t / EU_ou = Z_doisPARA_t^dois / Z₁PARA_ou^dois

Por meio dessas expressões, R e T são obtidos em termos da impedância acústica Z.

Coeficientes de transmissão e reflexão

O quociente acima é precisamente o coeficiente de transmissão:

T = (Z_dois/ Z₁) [2.Z₁/ (Z₁ +Z_dois)]^dois = 4Z₁Z_dois / (Z₁ +Z_dois)^dois

Uma vez que nenhuma perda é contemplada, é verdade que a intensidade do incidente é a soma da intensidade transmitida e da intensidade refletida:

eu_ou = Eu_r + eu_t → (eu_r / EU_ou) + (I_t / EU_ou) = 1

Isso nos permite encontrar uma expressão para o coeficiente de reflexão em termos das impedâncias dos dois meios:

R + T = 1 → R = 1 - T

Fazendo um pouco de álgebra para reorganizar os termos, o coeficiente de reflexão é:

R = 1 - 4Z₁Z_dois / (Z₁ +Z_dois)^dois = (Z₁ - Z_dois)^dois/ (Z₁ +Z_dois)^dois

E como a informação relacionada ao segundo meio é encontrada no pulso refletido, o coeficiente de reflexão é de grande interesse..

Assim, quando os dois meios apresentam uma grande diferença de impedância, o numerador da expressão anterior torna-se maior. Então, a intensidade da onda refletida é alta e contém boas informações sobre o meio..

Quanto à parte da onda transmitida a esse segundo meio, ela gradualmente se desvanece e a energia se dissipa como calor..

Aplicações e exercícios

Os fenômenos de transmissão e reflexão dão origem a várias aplicações muito importantes, por exemplo o sonar desenvolvido durante a Segunda Guerra Mundial e usado para detectar objetos. A propósito, alguns mamíferos como morcegos e golfinhos têm um sistema de sonar embutido.

Essas propriedades também são amplamente utilizadas para estudar o interior da Terra em métodos de prospecção sísmica, em imagens médicas de ultrassom, medição de densidade óssea e imagens de diferentes estruturas para falhas e defeitos..

A impedância acústica também é um parâmetro importante na avaliação da resposta sonora de um instrumento musical..

- Exercício 1 resolvido

A técnica de ultrassom para criar imagens de tecidos biológicos faz uso de pulsos de som de alta frequência. Os ecos contêm informações sobre os órgãos e tecidos pelos quais passam, que um software é responsável por traduzir em uma imagem.

Um pulso de ultrassom direcionado à interface músculo-gordura é incisado. Com os dados fornecidos, encontre:

a) A impedância acústica de cada tecido.

b) A porcentagem de ultrassom refletida na interface entre gordura e músculo.

Graxa

• Densidade: 952 kg / m³
• Velocidade do som: 1450 m / s

Músculo

• Densidade: 1075 kg / m³
• Velocidade do som: 1590 m / s

Solução para

A impedância acústica de cada tecido é encontrada substituindo na fórmula:

Z = ρ.v

Desta maneira:

Z_graxa = 952 kg / m³ x 1450 m / s = 1,38 x 10⁶ kg / m^dois.s

Z_músculo = 1075 kg / m³ x 1590 m / s = 1,71 x 10⁶  kg / m^dois.s

Solução b

Para encontrar a porcentagem de intensidade refletida na interface dos dois tecidos, é feito uso do coeficiente de reflexão dado por:

R = (Z₁ - Z_dois)^dois/ (Z₁ +Z_dois)^dois

Aqui Z_graxa = Z₁ e Z_músculo = Z_dois. O coeficiente de reflexão é uma quantidade positiva, que é garantida pelos quadrados da equação.

Substituindo e avaliando:

R = (1,38 x 10⁶ - 1,71 x 10⁶ )^dois  / (1,38 x 10⁶ + 1,71 x 10⁶ )^dois = 0,0114.

Ao multiplicar por 100 teremos o percentual refletido: 1,14% da intensidade do incidente.

- Exercício resolvido 2

Uma onda sonora tem um nível de intensidade de 100 decibéis e normalmente cai na superfície da água. Determine o nível de intensidade da onda transmitida e da onda refletida.

Dados:

Água

• Densidade: 1000 kg / m³
• Velocidade do som: 1430 m / s

Ar

• Densidade: 1,3 kg / m³
• Velocidade do som: 330 m / s

Solução

O nível de intensidade em decibéis de uma onda sonora, é denotado como L, é adimensional e é dado pela fórmula:

L = 10 log (I / 10^-12)

Aumentando para 10 em ambos os lados:

10 ^{L / 10} = I / 10^-12

Como L = 100, resulta em:

I / 10^-12 = 10¹⁰

As unidades de intensidade são dadas em termos de potência por unidade de área. No Sistema Internacional são Watt / m^dois. Portanto, a intensidade da onda incidente é:

eu_ou = 10¹⁰ . 10^-12 = 0,01 W / m^dois.

Para encontrar a intensidade da onda transmitida, o coeficiente de transmissão é calculado e, em seguida, multiplicado pela intensidade do incidente.

As respectivas impedâncias são:

Z_Água = 1000 kg / m³ x 1430 m / s = 1,43 x 10⁶ kg / m^dois.s

Z_ar = 1,3 kg / m³ x 330 m / s = 429 kg / m^dois.s

Substituindo e avaliando em:

T = 4Z₁Z_dois / (Z₁ +Z_dois)^dois = 4 × 1,43 x 10⁶ x 429 / (1,43 x 10⁶ + 429)^dois = 1,12 x 10^-3

Portanto, a intensidade da onda transmitida é:

eu_t = 1,12 x 10^-3 x 0,01 W / m^dois = 1,12 x 10^-5 W / m^dois

Seu nível de intensidade em decibéis é calculado por:

eu_t = 10 log (I_t / 10^-12) = 10 log (1,12 x 10^-5 / 10^-12) = 70,3 dB

Por sua vez, o coeficiente de reflexão é:

R = 1 - T = 0,99888

Com isso, a intensidade da onda refletida é:

eu_r = 0,99888 x 0,01 W / m^dois = 9,99 x 10^-3 W / m^dois

E seu nível de intensidade é:

eu_t = 10 log (I_r / 10^-12) = 10 log (9,99 x 10^-3 / 10^-12) = 100 dB

Referências

1. Andriessen, M. 2003. HSC Physics Course. Jacarandá.
2. Baranek, L. 1969. Acoustics. Segunda edição. Editorial Hispano Americana.
3. Kinsler, L. 2000. Fundamentals of Acoustics. Wiley and Sons.
4. Lowrie, W. 2007. Fundamentals of Geophysics. 2ª Edição. Cambridge University Press.
5. Wikipedia. Impedância acústica. Recuperado de: en.wikipedia.org.