O reatância capacitiva é a resistência que um capacitor, elemento regulador do fluxo de carga em um circuito de corrente alternada, opõe à passagem da corrente.
Em um circuito composto por um capacitor e ativado por uma fonte de corrente alternada, a reatância capacitiva X pode ser definidaC da seguinte maneira:
XC = 1 / ωC
Ou também:
XC = 1 / 2πfC
Onde C é a capacidade do capacitor e ω é a frequência angular da fonte, em relação à frequência f por:
ω = 2πf
A reatância capacitiva depende do inverso da frequência, portanto, em altas frequências ela tende a ser pequena, enquanto em baixas frequências, a reatância é grande.
A unidade do Sistema Internacional para medir a reatância capacitiva é o ohm (Ω), desde que a capacitância C do capacitor esteja em farad, (abreviado F) e a frequência seja expressa em segundos inversos (s-1).
Enquanto dura a carga, uma tensão e uma corrente alternadas são estabelecidas através do capacitor, cujas amplitudes ou valores máximos, denotados respectivamente como VC e euC, estão relacionados por reatância capacitiva analogamente à lei de Ohm:
VC = EuC ⋅ XC
Em um capacitor, a tensão está 90º atrás da corrente, ou a corrente está 90º à frente da corrente, como você preferir. Em qualquer caso, a frequência é a mesma.
Quando XC é muito grande, a corrente tende a ser pequena e fazendo com que o valor de X tenda ao infinitoC, o capacitor se comporta como um circuito aberto e a corrente é zero.
Índice do artigo
Vamos ver um exemplo de como calcular a reatância capacitiva: suponha que um capacitor de 6 μF esteja conectado a uma tomada CA de 40 V e frequência F 60 Hz.
Para encontrar a reatância capacitiva, é usada a definição dada no início. A frequência angular ω é dada por:
ω = 2πf = 2π x 60 Hz = 377 s-1
Então, este resultado é substituído na definição:
XC = 1 / ωC = 1 / (377 s-1x 6 x 10 -6 F) = 442,1 ohm
Agora vamos ver a amplitude da corrente fluindo no circuito. Uma vez que a fonte oferece uma tensão de amplitude VC = 40 V, usamos a relação entre reatância capacitiva, corrente e tensão para calcular a amplitude da corrente ou corrente máxima:
euC = VC / XC = 40 V / 442,1 ohm = 0,09047 A = 90,5 m A.
Se a frequência se torna muito grande, a reatância capacitiva torna-se pequena, mas se a frequência for 0 e tivermos uma corrente contínua, a reatância tenderia a ser infinita..
Quando um capacitor é conectado a uma fonte de corrente alternada, conforme ele oscila e muda sua polaridade, o capacitor experimenta cargas e descargas alternadas..
Para uma frequência de 60 Hz como a do exemplo, a voltagem é positiva 60 vezes por segundo e negativa outras 60 vezes por segundo.
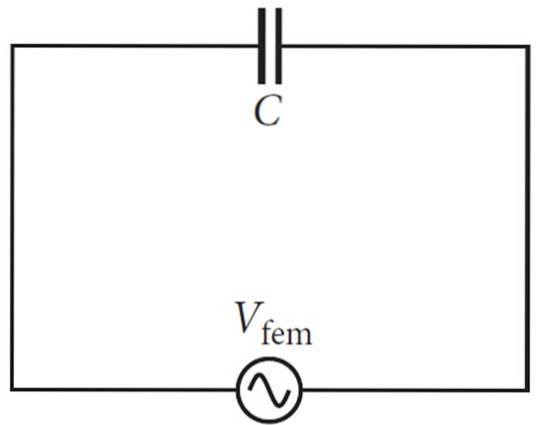
O aumento da tensão empurra a corrente para um lado, mas se o capacitor está descarregando, a corrente é produzida na direção oposta à da primeira..
Se vC (t) = Vm sen ωt, sabendo que a capacidade é a relação entre a carga e a tensão, teremos a carga:
C = q / V → q (t) = CV = CVm sen ωt
E tendo a carga em função do tempo, teremos a corrente, que é a derivada disso:
euC(t) = CVm ω cos ωt
Mas o seno e o cosseno são relacionados por: cos α = sin (α + π / 2), portanto:
euC(t) = CVm ω sin (ωt + π / 2) = IC sin (ωt + π / 2)
Com euC = CVC ω
Como você pode ver, há uma diferença de 90º de avanço da corrente em relação à tensão, como foi comentado no início.
Na descrição deste tipo de circuitos, o conceito de fasor, que é muito semelhante a um vetor e permite que qualquer quantidade alternada, como corrente, tensão ou impedância seja representada no plano complexo.
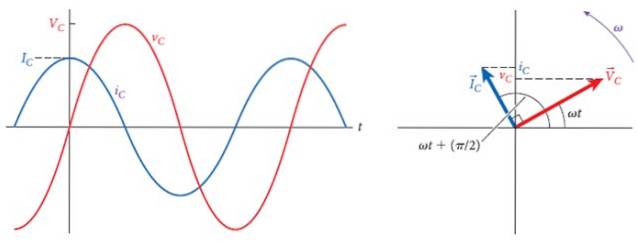
A figura a seguir mostra, à direita, os fasores de tensão e corrente no capacitor, que formam um ângulo de 90º entre eles, que é a diferença de fase entre os dois..
À esquerda estão os respectivos gráficos, de diferentes amplitudes, mas na mesma frequência. Com o tempo, a corrente vai à frente da tensão e quando é máxima, a corrente é zero e quando a tensão é zero, a corrente é máxima, mas com a polaridade invertida.
Em um circuito com resistores, capacitores e indutâncias, a reatância é a parte imaginária da impedância Z, uma grandeza complexa que nos circuitos de corrente alternada tem um papel semelhante ao da resistência elétrica para os circuitos de corrente contínua..
Na verdade, a impedância de um circuito é definida como a razão entre a tensão e a corrente:
Z = V / I
Para um capacitor ou capacitor, sua impedância é dada pelo quociente:
ZC = v (t) / i (t) = VC sin ωt / IC sin (ωt + π / 2)
Uma maneira de expressar a tensão e a corrente como fasores é indicando a amplitude e o ângulo de fase (forma polar):
v (t) = VC ∠ 0º
i (t) = IC ∠ 90º
Portanto:
ZC = VC ∠ 0º / IC ∠ 90º = (VC / EUC) ∠ 0º -90º =
= VC / CVC ω ∠ -90º = (1 / ωC) ∠ -90º =
ZC = (- j) XC
Ou seja, a impedância do capacitor é sua reatância capacitiva multiplicada pelo negativo da unidade imaginária.
A impedância de um circuito de corrente alternada com resistores, capacitores e indutores também pode ser representada binomialmente por:
Z = R + jX
Nessa equação, R representa a resistência, que corresponde à parte real, j é a unidade imaginária e X é a reatância, que pode ser capacitiva ou indutiva ou uma combinação de ambas, se esses elementos estiverem presentes ao mesmo tempo no o circuito.
Se o circuito contém um resistor e um capacitor em série, sua impedância é:
Z = ZR + ZC
Uma vez que na resistência a tensão e a corrente estão em fase, a impedância resistiva é simplesmente o valor da resistência R.
No caso da impedância capacitiva, já vimos que ZC = -jXC , portanto, a impedância do circuito RC é:
Z = R - jXC = R - j (1 / ωC)
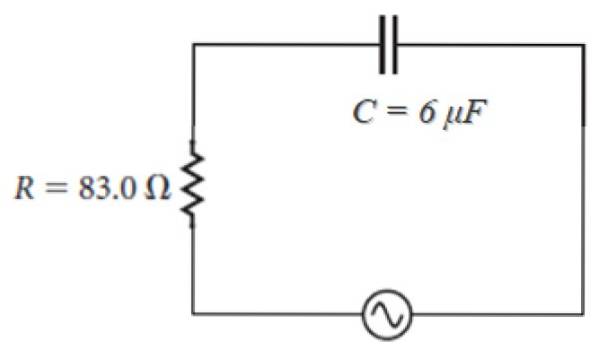
Por exemplo, no circuito mostrado abaixo, cuja fonte tem a forma:
100 V ⋅ sin (120πt)
Observando que ω = 120π, a impedância é:
Z = 83,0 - j [(1 / (120π ⋅ 6 x 10-6)] ohm = 83,0 - 442,1 j ohm.
Filtros passa-alta, filtros passa-baixa, circuitos do tipo ponte para medição de capacitâncias e indutâncias e circuitos de mudança de fase estão entre as principais aplicações de circuitos contendo reatâncias capacitivas, em combinação com indutâncias e resistências elétricas..
Em aparelhos de som, alguns alto-falantes vêm com alto-falantes separados. woofer (maior) para baixas frequências e tweeter ou buzina pequena para altas frequências. Isso melhora o desempenho e a qualidade do áudio.
Eles usam capacitores que impedem a chegada de baixas frequências no tweeter, enquanto no woofer é adicionado um indutor para evitar sinais de alta frequência, já que a indutância tem uma reatância proporcional à frequência: Xeu = 2πfL.
Ainda sem comentários