
O que é um geóide?
O geóide A figura da Terra é a superfície teórica do nosso planeta, determinada pelo nível médio dos oceanos e com uma forma bastante irregular. Matematicamente é definida como a superfície equipotencial do potencial gravitacional efetivo da Terra, ao nível do mar..
Por ser uma superfície imaginária (imaterial), atravessa continentes e montanhas, como se todos os oceanos estivessem ligados por canais de água que passam por massas de terra..

A Terra não é uma esfera perfeita, pois a rotação em torno de seu eixo a transforma em uma espécie de bola achatada pelos pólos, com vales e montanhas. É por isso que a forma esferóide ainda é imprecisa.
Esta mesma rotação adiciona uma força centrífuga à força da gravidade da Terra, cuja força resultante ou efetiva não aponta para o centro da Terra, mas tem um certo potencial gravitacional associado a ela..
Somado a isso, os acidentes geográficos criam irregularidades na densidade e, portanto, a força gravitacional de atração em algumas áreas deixa definitivamente de ser central..
Assim, os cientistas, começando com C. F. Gauss, que idealizou o geóide original em 1828, criaram um modelo geométrico e matemático para representar a superfície da Terra com mais precisão..
Para isso, assume-se um oceano em repouso, sem marés ou correntes oceânicas e com densidade constante, cuja altura serve de referência. A superfície da Terra é então considerada como uma ondulação suave, subindo onde a gravidade local é maior e afundando quando diminui.
Nessas condições, deixe a aceleração da gravidade efetiva sempre ser perpendicular à superfície cujos pontos estão no mesmo potencial e o resultado é o geóide, que é irregular, pois o equipotencial não é simétrico.
Índice do artigo
- 1 Fundação física do geóide
- 1.1 O potencial gravitacional da Terra
- 2 Diferenças entre geóide e elipsóide
- 2.1 As ondulações do geóide
- 3 vantagens de representar a Terra como um geóide
- 4 referências
Fundação física do geóide
Para determinar a forma do geóide, que foi refinada ao longo do tempo, os cientistas realizaram várias medições, levando em consideração dois fatores:
- O primeiro é que o valor de g, o campo gravitacional da Terra equivalente à aceleração da gravidade, depende da latitude: máximo nos pólos e mínimo no equador.
- A segunda é que, como dissemos antes, a densidade da Terra não é homogênea. Tem locais que aumenta porque as rochas são mais densas, há acúmulo de magma ou há muito solo na superfície, como uma montanha por exemplo.
Onde a densidade é maior, g então é isso. Observe que g é um vetor e é por isso que é denotado em negrito.
O potencial gravitacional da Terra
Para definir o geóide, é necessário o potencial devido à gravidade, para o qual o campo gravitacional deve ser definido como a força gravitacional por unidade de massa.
Se uma massa de teste m é colocado no referido campo, a força exercida pela Terra sobre ele é o seu peso P = mg, portanto a magnitude do campo é:
Força / massa = P / m = g
Já sabemos seu valor médio: 9,8 m / sdois e se a Terra fosse esférica, seria direcionada para o seu centro. Da mesma forma, de acordo com a lei da gravitação universal de Newton:
P = Gm M / rdois
Onde M é a massa da Terra e G é a constante universal de gravitação. Então, a magnitude do campo gravitacional g isso é:
g = GM / rdois
Ele se parece muito com um campo eletrostático, então um potencial gravitacional pode ser definido que é análogo ao eletrostático:
V = -GM / r
A constante G é a constante universal da gravitação. Bem, as superfícies nas quais o potencial gravitacional sempre tem o mesmo valor são chamadas de superfícies equipotenciais Y g é sempre perpendicular a eles, como disse antes.
Para esta classe particular de potencial, as superfícies equipotenciais são esferas concêntricas. O trabalho necessário para mover uma massa sobre eles é zero, porque a força é sempre perpendicular a qualquer caminho no equipotencial.
Componente lateral da aceleração da gravidade
Como a Terra não é esférica, a aceleração da gravidade deve ter um componente lateral geu devido à aceleração centrífuga, causada pelo movimento rotacional do planeta em torno de seu eixo.
A figura a seguir mostra este componente em verde, cuja magnitude é:
geu = ωdoispara
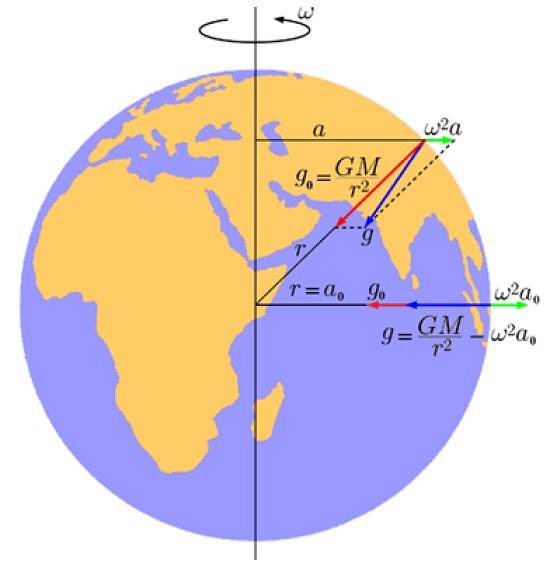
Nesta equação ω é a velocidade angular de rotação da Terra e para é a distância entre o ponto na Terra, em uma determinada latitude, e o eixo.
E em vermelho está o componente que é devido à atração gravitacional planetária:
gou = GM / rdois
Como resultado, por adição de vetor gou + geu, uma aceleração resultante ocorre g (em azul) que é a verdadeira aceleração da gravidade da Terra (ou aceleração efetiva) e que, como vemos, não aponta exatamente para o centro.
Além disso, a componente lateral depende da latitude: é zero nos pólos e, portanto, o campo gravitacional é máximo lá. No equador se opõe à atração gravitacional, reduzindo a gravidade efetiva, cuja magnitude permanece:
g = GM / rdois - ωdoisR
Com R = raio equatorial da Terra.
Entende-se agora que as superfícies equipotenciais da Terra não são esféricas, mas assumem uma forma tal que g sempre estar perpendicular a eles em todos os pontos.
Diferenças entre geóide e elipsóide
Aqui está o segundo fator que afeta a variação do campo gravitacional da Terra: as variações locais da gravidade. Existem lugares onde a gravidade aumenta porque há mais massa, por exemplo, na colina na figura a).
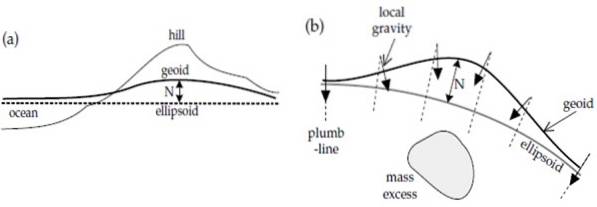
Ou existe um acúmulo ou excesso de massa abaixo da superfície, como em b). Em ambos os casos há uma elevação no geóide porque quanto maior a massa, maior a intensidade do campo gravitacional..
Por outro lado, sobre o oceano, a densidade é menor e como consequência o geóide afunda, como vemos à esquerda da figura a), acima do oceano..
Da figura b) também pode ser visto que a gravidade local, indicada com setas, é sempre perpendicular à superfície do geóide, como já dissemos. Isso nem sempre acontece com o elipsóide de referência.
As ondulações do geóide
A figura também indica, com uma seta bidirecional, a diferença de altura entre o geóide e o elipsóide, que é denominado ondulação y é denotado como N. As ondulações positivas estão relacionadas ao excesso de massa e as ondulações negativas aos defeitos.
As ondulações dificilmente ultrapassam os 200 m. Na verdade, os valores dependem de como é escolhido o nível do mar que serve de referência, já que alguns países escolhem de forma diferente de acordo com suas características regionais..
Vantagens de representar a Terra como um geóide
-No geóide o potencial efetivo, o resultado do potencial devido à gravidade e ao potencial centrífugo, é constante.
-A força da gravidade sempre atua perpendicularmente ao geóide e o horizonte é sempre tangencial a ele.
-O geóide oferece uma referência para aplicações de mapeamento de alta precisão.
-Usando o geóide, os sismólogos podem detectar a profundidade em que ocorrem os terremotos.
-O posicionamento do GPS depende do geóide a ser usado como referência.
-A superfície do oceano também é paralela ao geóide.
-As elevações e descidas do geóide indicam os excessos ou defeitos de massa, que são os anomalias gravimétricas. Quando uma anomalia é detectada e dependendo do seu valor, é possível inferir a estrutura geológica do subsolo, pelo menos em determinadas profundidades..
Esta é a base dos métodos gravimétricos em geofísica. Uma anomalia gravimétrica pode indicar acúmulos de certos minerais, estruturas enterradas ou mesmo espaços vazios. As cúpulas de sal no subsolo, detectáveis por métodos gravimétricos, são indicativas em alguns casos da presença de óleo..
Referências
- NAQUELA. Euronews. O controle da gravidade sobre a Terra. Recuperado de: youtube.com.
- ALEGRIA. Geóide. Recuperado de: youtube.com.
- Griem-Klee, S. Explorações de mineração: gravimetria. Recuperado de: geovirtual2.cl.
- Lowrie, W. 2007. Fundamentals of Geophysics. 2ª Edição. Cambridge University Press.
- NOAA. Qual é o geóide? Recuperado de: geodesy.noaa.gov.
- Sheriff, R. 1990. Applied Geophysics. 2ª Edição. Cambridge University Press.



Ainda sem comentários