UMA icoságono ou isodecágono é um polígono com 20 lados. Um polígono é uma figura plana formada por uma sequência finita de segmentos de linha (mais de dois) que circundam uma região do plano.
Cada segmento de linha é chamado de lado e a interseção de cada par de lados é chamada de vértice. De acordo com o número de lados, os polígonos recebem nomes específicos.
Os mais comuns são triângulo, quadrilátero, pentágono e hexágono, que possuem 3, 4, 5 e 6 lados respectivamente, mas podem ser construídos com a quantidade de lados que você quiser.
Abaixo estão algumas características dos polígonos e sua aplicação em um icoságono.
Um icoságono, sendo um polígono, pode ser classificado como regular e irregular, onde a palavra regular se refere ao fato de que todos os lados têm o mesmo comprimento e os ângulos internos medem todos iguais; caso contrário, diz-se que o icoságono (polígono) é irregular.
O icoságono regular também é chamado de isodecágono regular, porque para obter um icoságono regular o que você deve fazer é separar (dividir em duas partes iguais) cada lado de um decágono regular (polígono de 10 lados).
Para calcular o perímetro "P" de um polígono regular, o número de lados é multiplicado pelo comprimento de cada lado.
No caso particular de um icoságono, o perímetro é igual a 20xL, onde "L" é o comprimento de cada lado.
Por exemplo, se você tem um icoságono regular com um lado de 3cm, seu perímetro é igual a 20x3cm = 60cm.
É claro que, se o isogon for irregular, a fórmula acima não pode ser aplicada.
Nesse caso, os 20 lados devem ser somados separadamente para obter o perímetro, ou seja, o perímetro “P” é igual a ∑Li, com i = 1,2,…, 20.
O número de diagonais "D" que um polígono possui é igual a n (n-3) / 2, onde n representa o número de lados.
No caso de um icoságono, segue-se que tem D = 20x (17) / 2 = 170 diagonais.
Existe uma fórmula que ajuda a calcular a soma dos ângulos internos de um polígono regular, que pode ser aplicada a um icoságono regular.
A fórmula consiste em subtrair 2 do número de lados do polígono e depois multiplicar este número por 180º.
A forma como esta fórmula é obtida é que podemos dividir um polígono com n lados em n-2 triângulos, e usando o fato de que a soma dos ângulos internos de um triângulo é 180º obtemos a fórmula.
A imagem a seguir ilustra a fórmula para um enegon regular (polígono de 9 lados).
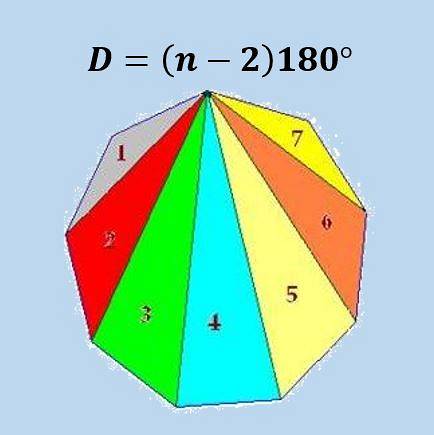
Usando a fórmula acima, obtém-se que a soma dos ângulos internos de qualquer icoságono é 18 × 180º = 3240º ou 18π.
Para calcular a área de um polígono regular é muito útil conhecer o conceito de apótema. O apótema é uma linha perpendicular que vai do centro do polígono regular ao ponto médio de qualquer um de seus lados.
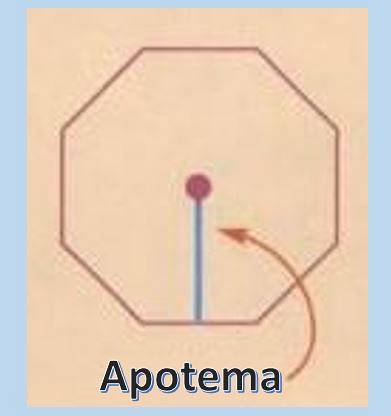
Uma vez que o comprimento do apótema é conhecido, a área de um polígono regular é A = Pxa / 2, onde "P" representa o perímetro e "a" o apótema..
No caso de um icoságono regular, sua área é A = 20xLxa / 2 = 10xLxa, onde “L” é o comprimento de cada lado e “a” é seu apótema.
Por outro lado, se você tiver um polígono irregular com n lados, para calcular sua área, divida o polígono em n-2 triângulos conhecidos, então calcule a área de cada um desses n-2 triângulos e finalmente adicione todas essas áreas.
O método descrito acima é conhecido como triangulação de um polígono.
Ainda sem comentários