
O que são números triangulares? Propriedades e demonstrações

É conhecido como números triangulares à seqüência de números que são obtidos fazendo um arranjo ou figura de pontos na forma de um triângulo equilátero. Os primeiros na sequência são: 1, 3, 6, 10, 15, 21, ...
O primeiro número triangular é 1, o segundo é 3, porque é obtido somando uma linha de dois pontos ao anterior, para formar um triângulo equilátero de três elementos.
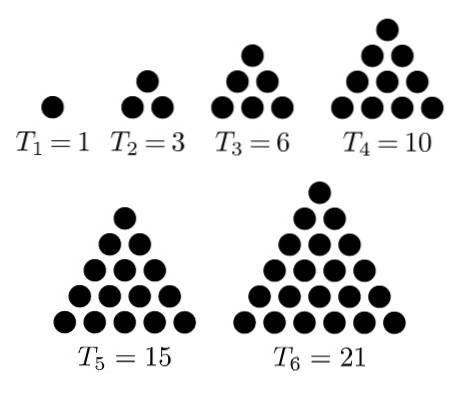
O terceiro é o 6, que surge ao adicionar uma linha de três pontos ao arranjo anterior, de forma que se forma um triângulo de três pontos por lado. O 10 da sequência é obtido adicionando outra linha ao arranjo anterior de modo que um triângulo de quatro pontos de cada lado seja formado.
A fórmula que permite encontrar o elemento n da sequência triangular, conhecido o número triangular anterior é:
Tn = Tn-1 + n
A lista dos seis primeiros números triangulares é obtida assim:
-Primeiro: 1
-Segundo: 1 + 2 = 3
-Terceiro: (1 +2) + 3 = 3 + 3 = 6
-Quarto: (1 + 2 + 3) + 4 = 6 + 4 = 10
-Quinto: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15
-Sexto: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21
Índice do artigo
- 1 Propriedades dos números triangulares
- 2 demonstrações
- 2.1 - Demonstração 1
- 2.2 - Demonstração 2
- 2.3 - Demonstração 3
- 2.4 - Demonstração 5
- 3 referências
Propriedades dos números triangulares
1.- O n-ésimo número triangular Tn da sequência de números triangulares é metade de n multiplicado por n + 1:
Tn = ½ n (n + 1)
2.- A soma do n-ésimo número triangular com o número triangular anterior, ou seja, o (n-1) -ésimo, é n ao quadrado:
Tn + Tn-1= ndois
3.- A diferença do n-ésimo número triangular menos o n-ésimo triangular menos um é n:
Tn - Tn-1 = n
4.- A soma dos primeiros n números triangulares é chamada de número tetraédrico Sn e é igual à sexta parte do produto de n multiplicado por (n + 1) e multiplicado por (n + 2):
Sn= ⅙ n (n + 1) (n + 2)
5.- Todo número natural N é o resultado da soma de três números triangulares:
N = Δ1 + Δ1 + Δ3
Esta última propriedade ou teorema, foi descoberta pelo grande matemático Carl Friedrich Gauss em 1796, que ele anotou em seu diário colocando a admiração dos gregos Eureka! que significa "Consegui".
Essa foi a mesma palavra usada muito antes pelo grego Arquimedes ao determinar o peso aparente de um corpo submerso..
Nessa relação, o número zero é considerado triangular e pode haver repetição.
Manifestações
- Demo 1
Prove que o número triangular n-esta:
Tn = ½ n (n + 1)
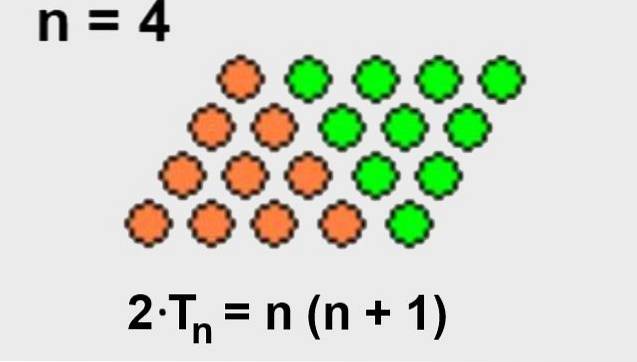
É fácil deduzir a fórmula acima, se percebermos que podemos adicionar um número igual de pontos ao arranjo triangular de forma que forme um quadrilátero de pontos.
Uma vez que o número total de pontos no arranjo quadrilateral é o número de linhas n multiplicado pelo número de colunas (n + 1), então o arranjo triangular terá apenas metade dos pontos do arranjo quadrilateral.
Aqui está ilustrado na figura 2.
- Demo 2
Mostre que a soma de n-número do triângulo com o n-th menos 1 número triangular é n ao quadrado:
Tn + Tn-1= ndois
Já foi mostrado que o número triangular n-isto é dado por:
Tn= ½ n (n + 1)
Portanto, o número triangular acima é:
Tn-1 = ½ (n-1) ((n-1) + 1) = ½ n (n - 1)
A soma de ambos é:
Tn + Tn-1 = ½ n (n + 1) + ½ n (n - 1)
O fator comum ½ n é usado para obter:
Tn + Tn-1 = ½ n [(n + 1) + (n - 1)] = ½ n [n + 1 + n - 1]
E imediatamente a expressão dentro do colchete é simplificada:
Tn + Tn-1 = ½ n [2 n] = ½ 2 n ⋅ n
Agora, lembrando que ½ vezes 2 é 1 e que n vezes n é n ao quadrado, temos:
Tn + Tn-1 = ndois
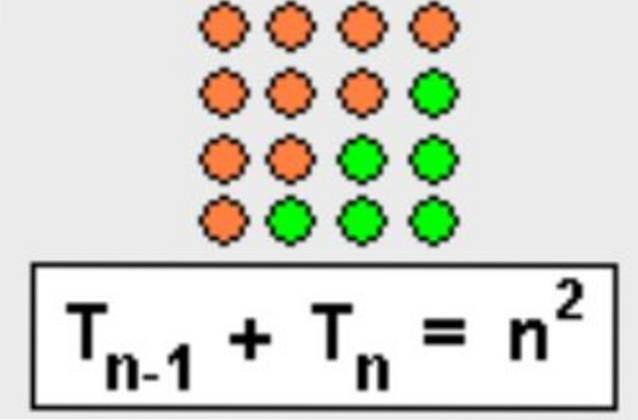
Esta propriedade também pode ser demonstrada de forma geométrica, basta completar o triângulo para formar um quadrado, conforme mostrado na figura 3.
- Demo 3
A diferença do número de ordem triangular n menos o número de ordem triangular n-1 é n:
Tn - Tn-1 = n
Isso pode ser comprovado simplesmente lembrando que o seguinte número triangular é obtido do anterior usando a fórmula:
Tn = Tn-1 + n
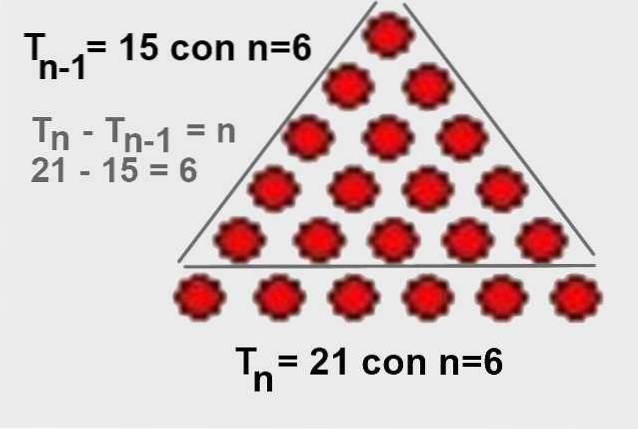
E a partir daí é evidente que Tn - Tn-1 = n. Também é fácil de visualizar graficamente, conforme mostrado na figura 4.
- Demo 5
A soma dos primeiros n números triangulares Sn é igual a um sexto do produto de n multiplicado por (n + 1) e multiplicado por (n + 2):
Sn = ⅙ n (n + 1) (n + 2)
Vamos usar o número triangular de ordem n: Tn= ½ n (n + 1). A soma do primeiro n números triangulares denotam-no por Sn
Por exemplo, S1 significa a soma do primeiro número triangular, que sem dúvida será 1.
A seguir, vamos ver se a fórmula que estamos tentando testar é verdadeira para n = 1:
S1 = ⅙ 1⋅2⋅3 = 1
Na verdade, a fórmula para n = 1 é verificada. É fácil visualizar que a soma dos primeiros n + 1 números triangulares será a soma do primeiro n mais o próximo número triangular:
Sn + 1 = Sn + Tn + 1
Agora suponha que a fórmula para Sn é verdadeiro para n, então o substituímos na expressão anterior e adicionamos o número triangular de ordem n + 1:
Sn + 1 = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]
Vamos ver passo a passo o que você obtém:
-Realizamos a soma das duas expressões fracionárias:
Sn + 1 = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] / 12
-É retirado do fator comum do numerador para 2 (n + 1) (n + 2) e simplifica:
Sn + 1 = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6
O resultado acima concorda com a fórmula para Sn se n for substituído por n + 1, o que foi mostrado por indução, a fórmula para a soma dos primeiros n termos triangulares.
Número tetraédrico
O resultado assim obtido é denominado número tetraédrico de ordem n, porque é como acumular camadas triangulares que formam um tetraedro, como mostrado na seguinte animação.

Referências
- Camacho J. Um aparecimento inesperado de números triangulares. Recuperado de: masscience.com
- Claudio. Números triangulares. Recuperado de: simplesmente números. Blogspot. com
- Wikipedia. Número triangular. Recuperado de: es.wikipedia.com
- Wikipedia. Número triangular. Recuperado de: en.wikipedia.com
- Wikipedia. Número tretraédrico. Recuperado de: en.wikipedia.com



Ainda sem comentários