
O que são vetores coplanares? (Com exercícios resolvidos)
O vetores coplanares ou coplanares são aqueles que estão contidos no mesmo plano. Quando existem apenas dois vetores, eles são sempre coplanares, visto que existem infinitos planos sempre é possível escolher aquele que os contenha..
Se você tiver três ou mais vetores, pode ser que alguns deles não estejam no mesmo plano que os outros, portanto, não podem ser considerados coplanares. A figura a seguir mostra um conjunto de vetores coplanares denotados em negrito PARA, B, C Y D:
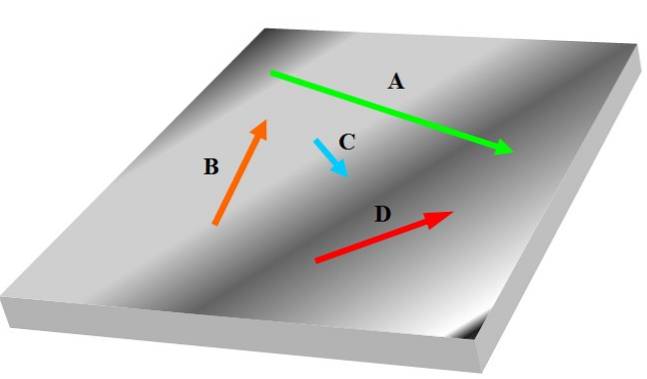
Os vetores estão relacionados ao comportamento e às propriedades de quantidades físicas relevantes na ciência e na engenharia; por exemplo, velocidade, aceleração e força.
Uma força produz efeitos diferentes em um objeto quando a forma como é aplicada varia, por exemplo, mudando a intensidade, direção e direção. Mesmo alterando apenas um desses parâmetros, os resultados são consideravelmente diferentes..
Em muitas aplicações, tanto em estática quanto em dinâmica, as forças que atuam sobre um corpo estão no mesmo plano, portanto, são consideradas coplanares..
Índice do artigo
- 1 Condições para os vetores serem coplanares
- 1.1 Produto misto entre três vetores
- 2 inscrições
- 2.1 Forças coplanares, concorrentes e não colineares
- 3 exercícios resolvidos
- 3.1 - Exercício 1
- 3.2 - Exercício 2
- 4 referências
Condições para os vetores serem coplanares
Para que três vetores sejam coplanares, eles devem estar no mesmo plano e isso acontece se atenderem a qualquer uma das seguintes condições:
-Os vetores são paralelos, portanto, seus componentes são proporcionais e linearmente dependentes.
-Seu produto misturado é nulo.
-Se você tiver três vetores e qualquer um deles puder ser escrito como uma combinação linear dos outros dois, esses vetores são coplanares. Por exemplo, um vetor que resulta da soma de dois outros, os três estão todos no mesmo plano.
Alternativamente, a condição de coplanaridade pode ser estabelecida da seguinte forma:
U V w são coplanares se houver três números (escalares) α, β, γ tais que αou + βv + γw = 0 com (α, β, γ) diferente de (0, 0, 0)
Produto misto entre três vetores
O produto misto entre vetores é definido por três vetores ou, v Y C, resultando em um escalar que resulta da realização da seguinte operação:
ou · (v x C) = ou · (v x C)
Primeiro, o produto vetorial que está entre parênteses é realizado: v x C, cujo resultado é um vetor normal (perpendicular) ao plano no qual ambos v o que C.
sim ou está no mesmo plano que v Y C, naturalmente o produto escalar (produto pontual) entre u e o referido vetor normal deve ser 0. Desta forma, verifica-se que os três vetores são coplanares (eles estão no mesmo plano).
Quando o produto misto não é zero, seu resultado é igual ao volume do paralelepípedo que possui os vetores ou, v Y C como lados adjacentes.
Formulários
Forças coplanares, concorrentes e não colineares
As forças concorrente todos eles são aplicados ao mesmo ponto. Se também forem coplanares, podem ser substituídos por um único, que é denominado força resultante e tem o mesmo efeito que as forças originais.
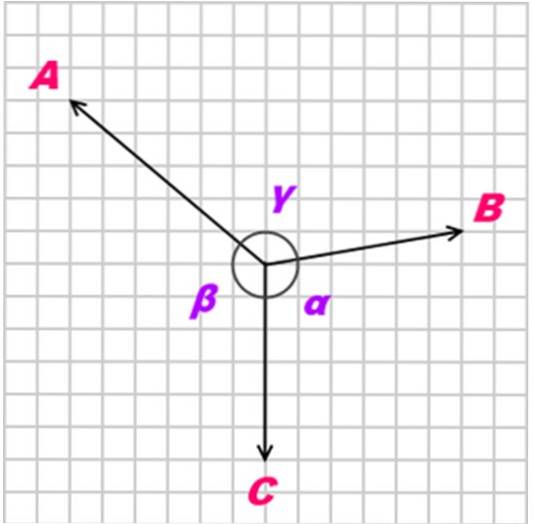
Se um corpo está em equilíbrio graças a três forças coplanares, concorrentes e não colineares (não paralelas), chamadas PARA, B Y C, a Teorema de Lamy aponta que a relação entre essas forças (magnitudes) é a seguinte:
A / sin α = B / sin β = C / sin γ
Com α, β e γ como ângulos opostos às forças aplicadas, conforme mostrado na figura a seguir:
Exercícios resolvidos
-Exercício 1
Encontre o valor de k para que os seguintes vetores sejam coplanares:
ou = <-3, k, 2>
v = <4, 1, 0>
C = <-1, 2, -1>
Solução
Como temos os componentes dos vetores, utiliza-se o critério do produto misto, portanto:
ou · (v x C) = 0
É resolvido primeiro v x C. Os vetores serão expressos em termos de vetores unitários eu, j Y k que distinguem as três direções perpendiculares no espaço (largura, altura e profundidade):
v= 4 eu + j + 0 k
C= -1 eu + doisj -1 k
v x w = -4 (i x i) + 8 (i x j) - 4 (i x k) - (j x i) + dois (j x j) - dois (j x k) = 8 k + 4 j + k -dois i = -dois eu + 4 j + 9 k
Agora consideramos o produto escalar entre u e o vetor que resultou da operação anterior, definindo a operação igual a 0:
ou (v x C) = (-3 eu + k j + dois k) · (-dois eu + 4 j + 9 k) = 6 + 4k +18 = 0
24 + 4k = 0
O valor procurado é: k = - 6
Então, o vetor ou isso é:
ou = <-3, -6, 2>
-Exercício dois
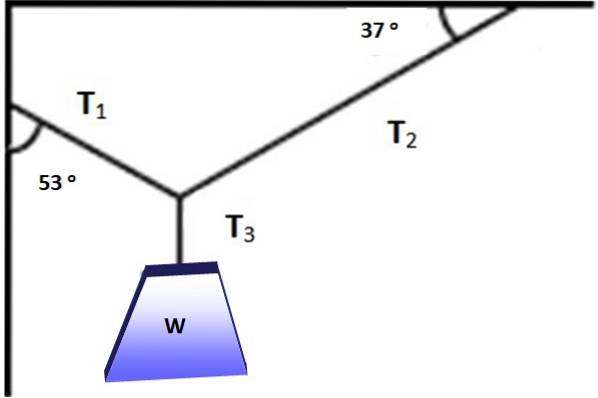
A figura mostra um objeto cujo peso é W = 600 N, pendurado em equilíbrio graças aos cabos colocados nos ângulos mostrados na figura 3. É possível aplicar o teorema de Lamy nesta situação? Em qualquer caso, encontre as magnitudes de T1, Tdois Y T3 que tornam o equilíbrio possível.
Solução
O teorema de Lamy é aplicável nesta situação se for considerado o nó no qual as três tensões são aplicadas, uma vez que constituem um sistema de forças coplanares. Em primeiro lugar, é feito o diagrama de corpo livre para o peso suspenso, a fim de determinar a magnitude de T3:
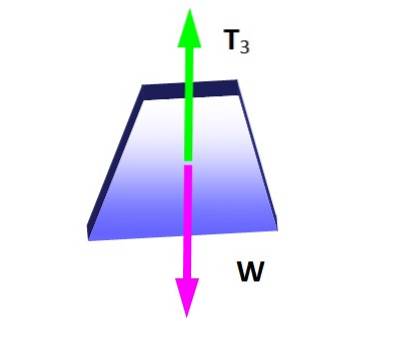
Da condição de equilíbrio segue-se que:
T3 = W = 600 N
Os ângulos entre as forças estão marcados em vermelho na figura a seguir, pode-se verificar facilmente que sua soma é 360º. Agora é possível aplicar o teorema de Lamy, já que uma das forças e os três ângulos entre elas são conhecidos:
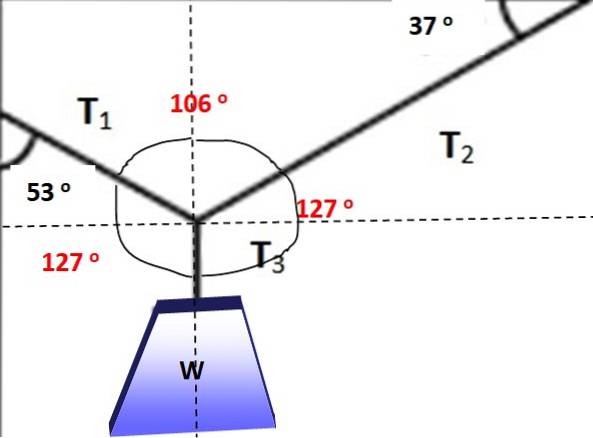
T1 / sin 127º = W / sin 106º
Portanto: T1 = sin 127º (W / sin 106º) = 498,5 N
Novamente, o teorema de Lamy é aplicado para resolver Tdois:
Tdois / sin 127 = T1 / sin 127º
Tdois = T1 = 498,5 N
Referências
- Figueroa, D. Série: Física para Ciências e Engenharia. Volume 1. Cinemática. 31-68.
- Fisica. Módulo 8: Vetores. Recuperado de: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mecânica para Engenheiros. Estático. 6ª Edição. Continental Publishing Company 28-66.
- McLean, W. Schaum Series. Mecânica para Engenheiros: Estática e Dinâmica. 3ª edição. McGraw Hill. 1-15.
- Wikipedia. Vetor. Recuperado de: es.wikipedia.org.



Ainda sem comentários