O tipos de integrais que encontramos no cálculo são as integrais indefinidas e as integrais definidas. Embora integrais definidos tenham muito mais aplicações do que integrais indefinidos, é necessário primeiro aprender como resolver integrais indefinidos..
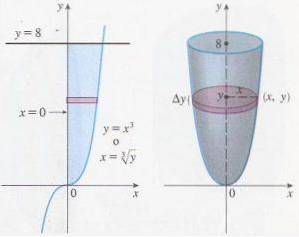
Uma das aplicações mais atraentes de integrais definidas é o cálculo do volume de um sólido de revolução. Ambos os tipos de integrais têm as mesmas propriedades de linearidade e também as técnicas de integração não dependem do tipo de integral.
Mas apesar de ser muito semelhante, há uma diferença principal; no primeiro tipo de integral o resultado é uma função (que não é específica), enquanto no segundo tipo o resultado é um número.
O mundo das integrais é muito amplo, mas dentro dele podemos distinguir dois tipos básicos de integrais, que têm grande aplicabilidade na vida cotidiana..
Se F '(x) = f (x) para todo x no domínio de f, dizemos que F (x) é uma antiderivada, uma primitiva ou uma integral de f (x).
Por outro lado, observemos que (F (x) + C) '= F' (x) = f (x), o que implica que a integral de uma função não é única, uma vez que atribui valores diferentes à constante C obteremos diferentes antiderivadas.
Por esta razão, F (x) + C é chamado de Integral Indefinido de f (x) e C é chamado de constante de integração e nós o escrevemos da seguinte maneira
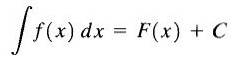
Como podemos ver, a integral indefinida da função f (x) é uma família de funções.
Por exemplo, se você deseja calcular a integral indefinida da função f (x) = 3x², você deve primeiro encontrar uma antiderivada de f (x).
É fácil ver que F (x) = x³ é uma antiderivada, pois F '(x) = 3x². Portanto, pode-se concluir que
∫f (x) dx = ∫3x²dx = x³ + C.
Seja y = f (x) uma função real contínua em um intervalo fechado [a, b] e seja F (x) uma antiderivada de f (x). A integral definida de f (x) entre os limites aeb é chamada de número F (b) -F (a), e é denotada da seguinte maneira
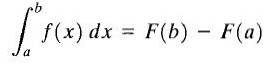
A fórmula mostrada acima é mais conhecida como "Teorema Fundamental do Cálculo". Aqui, "a" é chamado de limite inferior e "b" é chamado de limite superior. Como você pode ver, a integral definida de uma função é um número.
Neste caso, se calcularmos a integral definida de f (x) = 3x² no intervalo [0,3], obteremos um número.
Para determinar esse número, escolhemos F (x) = x³ como a antiderivada de f (x) = 3x². Então, calculamos F (3) -F (0) que nos dá o resultado 27-0 = 27. Em conclusão, a integral definida de f (x) no intervalo [0,3] é 27.
Pode-se notar que se G (x) = x³ + 3 for escolhido, então G (x) é uma antiderivada de f (x) diferente de F (x), mas isso não afeta o resultado uma vez que G (3) - G (0) = (27 + 3) - (3) = 27. Por este motivo, nas integrais definidas a constante de integração não aparece.
Uma das aplicações mais úteis deste tipo de integral é que permite calcular a área (volume) de uma figura plana (de um sólido de revolução), estabelecendo funções adequadas e limites de integração (e um eixo de rotação).
Dentro das integrais definidas podemos encontrar várias extensões dela, tais como integrais de linha, integrais de superfície, integrais impróprios, integrais múltiplos, entre outros, todos com aplicações muito úteis em ciência e engenharia..
Ainda sem comentários