
Linhas, equações e exemplos característicos oblíquos
As linhas oblíquas São aquelas que se inclinam, seja em relação a uma superfície plana, seja a outra reta que indique uma determinada direção. Como exemplo, considere as três linhas desenhadas em um plano que aparecem na figura a seguir.
Sabemos suas respectivas posições relativas porque as comparamos com uma linha de referência, que geralmente é a Eixo X denotando a horizontal.
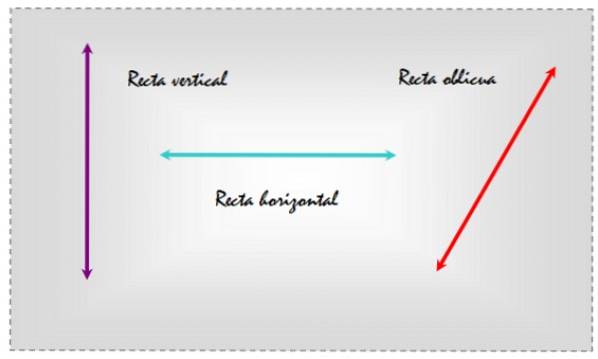
Desta forma, tendo como referência a horizontal, a linha da esquerda é vertical, a do centro é horizontal e a da direita é oblíqua, pois está inclinada em relação às linhas de referência do cotidiano..
Agora, as linhas que estão no mesmo plano, como a superfície do papel ou a tela, ocupam diferentes posições relativas uns aos outros, dependendo se eles se cruzam ou não. No primeiro caso, são linhas secantes, enquanto no segundo, são paralelas.
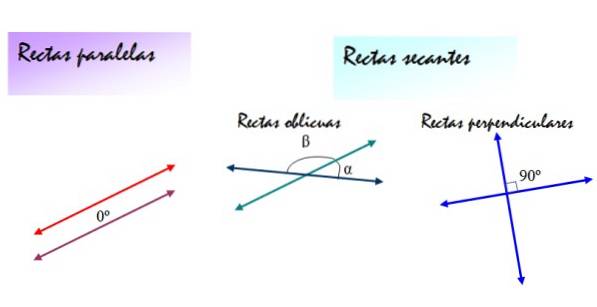
Por outro lado, as linhas secantes podem ser linhas oblíquas ou linhas perpendiculares. Em ambos os casos, as inclinações das retas são diferentes, mas as retas oblíquas formam entre si ângulos α e β, diferentes de 90º, enquanto os ângulos determinados pelas retas perpendiculares são sempre 90º..
A figura a seguir resume essas definições:
Índice do artigo
- 1 Equações
- 1.1 Equação da reta no plano
- 2 Exemplos de linhas oblíquas
- 2.1 Raios de luz
- 2.2 Linhas que não estão no mesmo plano
- 3 referências
Equações
Para saber as posições relativas das linhas no plano, é necessário saber o ângulo que elas formam entre si. Observe que as linhas são:
Paralelo: se eles têm a mesma inclinação (mesma direção) e nunca se cruzam, portanto, seus pontos são equidistantes.
Coincidente: quando todos os seus pontos coincidem e, portanto, têm a mesma inclinação, mas a distância entre seus pontos é zero.
Secagem: se suas inclinações são diferentes, a distância entre seus pontos varia e a interseção é um único ponto.
Portanto, uma maneira de saber se duas retas no plano são secantes ou paralelas é por meio de sua inclinação. Os critérios de paralelismo e perpendicularidade das linhas são os seguintes:
Seja L duas linhas1 e eudois pertencente a um plano, cujas inclinações são respectivamente m1 e mdois. Essas linhas são paralelas se m1 = mdois e são perpendiculares quando m1= -1 / mdois
Se, conhecendo as inclinações de duas retas no plano, nenhum dos critérios anteriores for atendido, concluímos que as retas são oblíquas. Conhecendo dois pontos de uma linha, a inclinação é calculada imediatamente, como veremos na próxima seção.
É possível descobrir se duas retas são secantes ou paralelas encontrando sua interseção, resolvendo o sistema de equações que elas formam: se há solução são secantes, se não há solução são paralelas, mas se as soluções são infinito, as linhas são coincidentes.
No entanto, este critério não nos informa sobre o ângulo entre essas linhas, mesmo que se cruzem.
Para saber o ângulo entre as linhas, dois vetores são necessários ou Y v que pertencem a cada um deles. Assim é possível saber o ângulo que eles formam por meio do produto escalar dos vetores, definidos desta forma:
ou•v =u.v.cos α
Equação da reta no plano
Uma linha no plano cartesiano pode ser representada de várias maneiras, como:
-Forma de declive-interceptação: sim m é a inclinação da linha e b é a intersecção da linha com o eixo vertical, a equação da linha é y = mx + b.
-Equação geral para uma linha reta: Axe + Por + C = 0, Onde m = A / B é a inclinação.
No plano cartesiano, as linhas verticais e horizontais são casos particulares da equação da linha..
-Linhas verticais: x = a
-Linhas horizontais: y = k
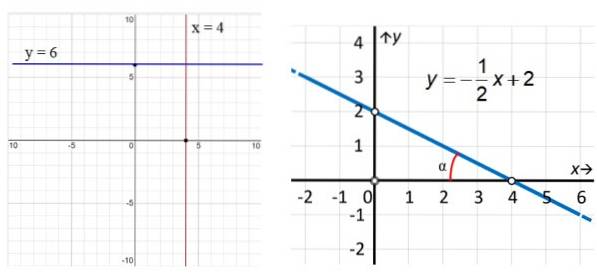
Nos exemplos da figura 3, a linha vertical vermelha tem a equação x = 4, enquanto a linha paralela ao eixo x (azul) tem a equação y = 6. Quanto à linha da direita, vemos que ela é oblíqua e encontrar sua equação usamos os pontos destacados na figura: (0,2) e (4,0) desta forma:
m = (edois - Y1) / (xdois - x1) = (2 - 0) / (0 - 4) = - ½
O corte desta linha com o eixo vertical é y = 2, como pode ser visto no gráfico. Com esta informação:
y = (-½) x + 2
É fácil determinar o ângulo de inclinação em relação ao eixo x. Eu sinto isso:
α = arctg (2/4) = 26,6º
Portanto, o ângulo positivo do eixo x à linha é: 180º - 26,6º = 153,4º
Exemplos de linhas oblíquas

Linhas oblíquas aparecem em muitos lugares, é uma questão de prestar atenção para encontrá-las na arquitetura, nos esportes, na fiação elétrica, nas tubulações e em muitos outros lugares. Na natureza, as linhas oblíquas também estão presentes, como veremos a seguir:
Raios de luz
A luz solar viaja em linha reta, mas a forma arredondada da Terra afeta como a luz solar atinge a superfície..
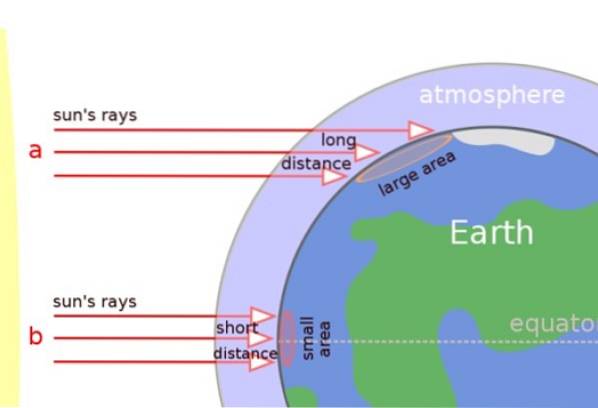
Na imagem abaixo podemos ver claramente que os raios solares atingem perpendicularmente nas regiões tropicais, mas, ao invés disso, atingem a superfície obliquamente nas regiões temperadas e nos pólos..
É por isso que os raios do sol viajam por uma distância maior na atmosfera e também o calor se espalha por uma superfície maior (veja a figura). O resultado é que as áreas próximas aos pólos são mais frias.
Linhas que não estão no mesmo plano
Quando duas linhas não estão no mesmo plano, elas ainda podem ser oblíquas ou empenado, como também são conhecidos. Neste caso, seus vetores diretores não são paralelos, mas como não pertencem ao mesmo plano, essas retas não se cruzam.
Por exemplo, as linhas na figura 6 à direita estão claramente em planos diferentes. Se você olhar para eles de cima, verá que eles realmente se cruzam, mas não têm um ponto em comum. À direita vemos as rodas da bicicleta, cujos raios parecem cruzar quando vistos de frente.

Referências
- Geometria. Vetor de diretor de uma linha. Recuperado de: juanbragado.es.
- Larson, R. 2006. Calculus with Analytical Geometry. 8º. Edição. Colina Mcgraw.
- A matemática é um jogo. Linhas e ângulos. Recuperado de: juntadeandalucia.es.
- Linhas retas que se cruzam. Recuperado de: profesoraltuna.com.
- Villena, M. Analytical Geometry in R3. Recuperado de: dspace.espol.edu.ec.



Ainda sem comentários