Redução de termos semelhantes (com exercícios resolvidos)

O redução de termos semelhantes é um método usado para simplificar expressões algébricas. Em uma expressão algébrica, termos semelhantes são aqueles que têm a mesma variável; ou seja, eles têm as mesmas incógnitas representadas por uma letra, e estes têm os mesmos expoentes.

Em alguns casos, os polinômios são extensos e, para chegar a uma solução, deve-se tentar reduzir a expressão; Isso é possível quando existem termos semelhantes, que podem ser combinados pela aplicação de operações e propriedades algébricas, como adição, subtração, multiplicação e divisão..

Índice do artigo

• 1 explicação
• 2 Como fazer uma redução de termos semelhantes?
  • 2.1 Exemplo
  • 2.2 Redução de termos semelhantes com sinais de igualdade
  • 2.3 Redução de termos semelhantes com sinais diferentes
• 3 Redução de termos semelhantes nas operações
  • 3.1 Em somas
  • 3.2 Em subtração
  • 3.3 Em multiplicação
  • 3.4 Em divisões
• 4 exercícios resolvidos
  • 4.1 Primeiro exercício
  • 4.2 Segundo exercício
• 5 referências

Explicação

Termos semelhantes são formados pelas mesmas variáveis ​​com os mesmos expoentes e, em alguns casos, estes são diferenciados apenas por seus coeficientes numéricos..

Termos semelhantes também são considerados aqueles que não possuem variáveis; ou seja, os termos que têm apenas constantes. Assim, por exemplo, os seguintes são termos semelhantes:

- 6x^dois - 3x^dois. Ambos os termos têm a mesma variável x^dois.

- 4º^doisb³ + 2ª^doisb³. Ambos os termos têm as mesmas variáveis ​​a^doisb³.

- 7 - 6. Os termos são constantes.

Esses termos que têm as mesmas variáveis, mas com expoentes diferentes são chamados de termos diferentes, como:

- 9a^doisb + 5ab. Variáveis ​​têm expoentes diferentes.

- 5x + e. As variáveis ​​são diferentes.

- b - 8. Um termo tem uma variável, o outro é uma constante.

Identificando os termos semelhantes que formam um polinômio, estes podem ser reduzidos a um, combinando todos aqueles que possuem as mesmas variáveis ​​com os mesmos expoentes. Desta forma, a expressão é simplificada reduzindo o número de termos que a compõem e o cálculo de sua solução é facilitado..

Como fazer uma redução de termos semelhantes?

A redução de termos semelhantes é feita aplicando-se a propriedade associativa de adição e a propriedade distributiva do produto. Usando o seguinte procedimento, você pode fazer uma redução de prazo:

- Os termos semelhantes são agrupados primeiro.

- Os coeficientes (os números que acompanham as variáveis) dos termos semelhantes são adicionados ou subtraídos, e as propriedades associativas, comutativas ou distributivas são aplicadas, conforme o caso..

- Em seguida, são escritos os novos termos obtidos, colocando-se na frente deles o sinal que resultou da operação..

Exemplo

Reduza os termos da seguinte expressão: 10x + 3y + 4x + 5y.

Solução

Primeiro, os termos são ordenados para agrupar aqueles que são semelhantes, aplicando a propriedade comutativa:

10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.

Em seguida, a propriedade distributiva é aplicada e os coeficientes que acompanham as variáveis ​​são adicionados para obter a redução dos termos:

10x + 4x + 3y + 5y

= (10 + 4) x + (3 + 5) y

= 14x + 8y.

Para reduzir termos semelhantes, é importante levar em consideração os sinais dos coeficientes que acompanham a variável. Existem três casos possíveis:

Redução de termos semelhantes com sinais de igual

Nesse caso, os coeficientes são somados e o sinal dos termos é colocado na frente do resultado. Portanto, se forem positivos, os termos resultantes serão positivos; caso os termos sejam negativos, o resultado terá o sinal (-) acompanhado da variável. Por exemplo:

a) 22ab^dois + 12ab^dois = 34 ab^dois.

b) -18x³ - 9x³ - 6 = -27x³ - 6.

Redução de termos semelhantes cem sinais diferentes

Nesse caso, os coeficientes são subtraídos e o sinal do maior coeficiente é colocado na frente do resultado. Por exemplo:

a) 15x^doisy - 4x^doise + 6x^doisy - 11x^doisY

= (15x^doise + 6x^doisy) + (- 4x^doisy - 11x^doisY)

= 21x^doisy + (-15x^doisY)

= 21x^doisy - 15x^doisY

= 6x^doisY.

b) -5a³b + 3 a³b - 4a³b + a³b

= (3 a³b + a³b) + (-5a³b - 4a³b)

= 4a³b - 9a³b

= -5 a³b.

Assim, para reduzir termos semelhantes que possuem sinais diferentes, um único termo aditivo é formado com todos aqueles que possuem sinal positivo (+), os coeficientes são somados e o resultado é acompanhado pelas variáveis.

Da mesma forma, forma-se um termo subtrativo, com todos os termos que têm sinal negativo (-), somam-se os coeficientes e o resultado é acompanhado pelas variáveis.

Finalmente, as somas dos dois termos formados são subtraídos, e o sinal do maior é colocado no resultado.

Redução de termos semelhantes nas operações

A redução de termos semelhantes é uma operação de álgebra, que pode ser aplicada em adição, subtração, multiplicação e divisão algébrica.

Em somas

Quando você tem vários polinômios com termos semelhantes, para reduzi-los, os termos de cada polinômio são ordenados mantendo seus sinais, então eles são escritos um após o outro e os termos semelhantes são reduzidos. Por exemplo, temos os seguintes polinômios:

3x - 4xy + 7x^doise + 5xy^dois.

- 6x^doisy - 2xy + 9 xy^dois - 8x.

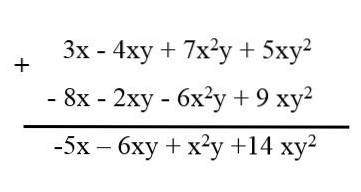
Em subtração

Para subtrair um polinômio de outro, o minuendo é escrito e então o subtraendo com seus sinais mudados, e então a redução dos termos semelhantes é feita. Por exemplo:

5 ª³ - 3ab^dois + 3b^doisc

6ab^dois + 2ª³ - 8b^doisc

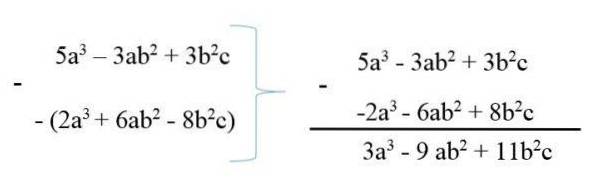
Assim, os polinômios são resumidos em 3a³ - 9ab^dois + 11b^doisc.

Em multiplicações

Em um produto de polinômios, os termos que compõem o multiplicando são multiplicados por cada termo que compõe o multiplicador, considerando que os sinais da multiplicação permanecem os mesmos se forem positivos.

Eles só serão alterados quando multiplicados por um termo negativo; ou seja, quando dois termos do mesmo sinal são multiplicados, o resultado será positivo (+), e quando eles tiverem sinais diferentes, o resultado será negativo (-).

Por exemplo:

a) (a + b) _* (a + b)

= a^dois + ab + ab + b^dois

= a^dois + 2ab + b^dois.

b) (a + b) _* (a - b)

= a^dois - ab + ab - b^dois

= a^dois - b^dois.

táxi) _* (a - b)

= a^dois - ab - ab + b^dois

= a^dois - 2ab + b^dois.

Em divisões

Quando você deseja reduzir dois polinômios por meio de uma divisão, você deve encontrar um terceiro polinômio que, quando multiplicado pelo segundo (divisor), resulta no primeiro polinômio (dividendo).

Para isso, os termos do dividendo e do divisor devem ser ordenados, da esquerda para a direita, de forma que as variáveis ​​em ambos estejam na mesma ordem.

Em seguida, é realizada a divisão, partindo do primeiro termo à esquerda do dividendo pelo primeiro termo à esquerda do divisor, sempre levando em consideração os sinais de cada termo..

Por exemplo, reduza o polinômio: 10x⁴ - 48x³e + 51x^doisY^dois + 4xy³ - 15 anos⁴ dividindo-o pelo polinômio: -5x^dois + 4xy + 3y^dois.

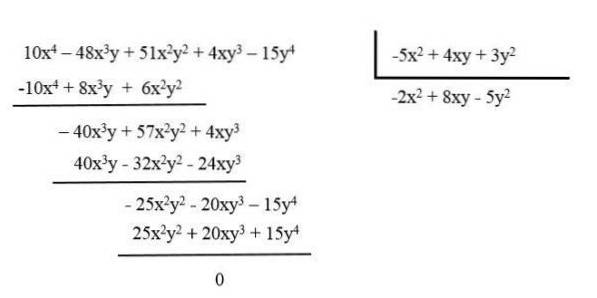
O polinômio resultante é -2x^dois + 8xy - 5y^dois.

Exercícios resolvidos

Primeiro exercício

Reduza os termos da expressão algébrica fornecida:

Dia 15^dois - 8ab + 6a^dois - 6ab - 9 + 4a^dois - 13 ab.

Solução

A propriedade comutativa de adição é aplicada, agrupando os termos que possuem as mesmas variáveis:

Dia 15^dois - 8ab + 6a^dois - 6ab + 9 + 4a^dois - 13

= (15a^dois + 6º^dois + 4º^dois) + (- 8ab - 6ab) + (9 - 13).

Em seguida, a propriedade distributiva da multiplicação é aplicada:

Dia 15^dois - 8ab + 6a^dois - 6ab + 9 + 4a^dois - 13

= (15 + 6 + 4) a^dois + (- 8 - 6) ab + (9 - 13).

Finalmente, eles são simplificados adicionando e subtraindo os coeficientes de cada termo:

Dia 15^dois - 8ab + 6a^dois - 6ab + 9 + 4a^dois - 13

= 25a^dois - 14ab - 4.

Segundo exercício

Simplifique o produto dos seguintes polinômios:

(8x³ + 7xy^dois)_*(8x³ - 7 xy^dois).

Solução

Cada termo do primeiro polinômio é multiplicado pelo segundo, levando em consideração que os sinais dos termos são diferentes; portanto, o resultado de sua multiplicação será negativo, assim como as leis dos expoentes devem ser aplicadas.

(8x³ + 7xy^dois) _* (8x³ - 7xy^dois)

= 64 x⁶ - 56 x³_* xy^dois + 56 x³_* xy^dois - 49 x^doisY⁴

= 64 x⁶ - 49 x^doisY⁴.

Referências

1. Angel, A. R. (2007). Álgebra elementar. Pearson Education,.
2. Baldor, A. (1941). Álgebra. Havana: cultura.
3. Jerome E. Kaufmann, K. L. (2011). Álgebra elementar e intermediária: uma abordagem combinada. Flórida: Cengage Learning.
4. Smith, S. A. (2000). Álgebra. Pearson Education.
5. Vigil, C. (2015). Álgebra e suas aplicações.