
Fórmula da regra de Simpson, prova, exemplos, exercícios
O regra dos simpsons é um método de calcular, de forma aproximada, integrais definidas. Baseia-se na divisão do intervalo de integração em um número par de subintervalos igualmente espaçados.
Os valores extremos de dois subintervalos consecutivos definem três pontos, pelos quais uma parábola, cuja equação é um polinômio de segundo grau, se ajusta.
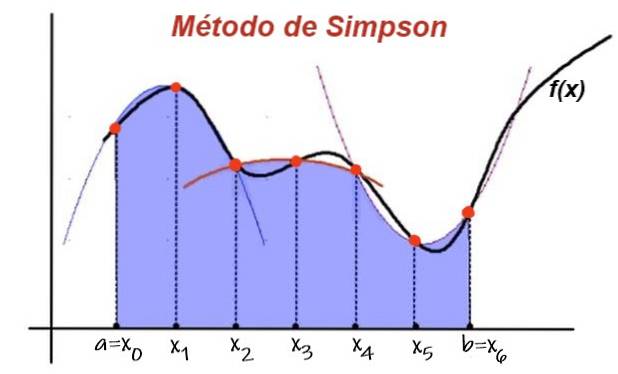
Então, a área sob a curva da função nos dois intervalos consecutivos é aproximada pela área do polinômio de interpolação. Somando a contribuição à área sob a parábola de todos os subintervalos sucessivos, temos o valor aproximado da integral.
Por outro lado, como a integral de uma parábola pode ser calculada algebricamente com exatidão, é possível encontrar uma fórmula analítica para o valor aproximado da integral definida. É conhecido como o Fórmula de Simpson.
O erro do resultado aproximado assim obtido diminui à medida que o número de subdivisões n é maior (onde n é um número par).
Uma expressão será dada a seguir que permite estimar o limite superior do erro da aproximação ao integral I, quando uma partição de n subintervalos regulares do intervalo total foi feita [a, b].
Índice do artigo
- 1 Fórmula
- 2 demo
- 2.1 Coeficientes do polinômio de interpolação
- 2.2 Cálculo da integral aproximada em [Xi, Xi + 2]
- 2.3 Cálculo aproximado da integral em [a, b]
- 2.4 Erro de aproximação
- 3 exemplos trabalhados
- 3.1 - Exemplo 1
- 3.2 - Exemplo 2
- 3.3 - Exemplo 3
- 4 Exercício proposto
- 5 referências
Fórmula
O intervalo de integração [a, b] é subdividido em n subintervalos com n sendo um número inteiro par. A largura de cada subdivisão será:
h = (b - a) / n
Desta forma, no intervalo [a, b] a partição é feita:
X0, X1, X2,…, Xn-1, Xn
Onde X0 = a, X1 = X0 + h, X2 = X0 + 2h,…, Xn-1 = X0 + (n-1) h, Xn = X0 + nh = b.
A fórmula que permite calcular de forma aproximada a integral definida I da função contínua, e preferencialmente suave, no intervalo [a, b] é:
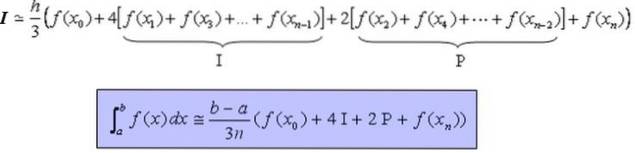
Demonstração
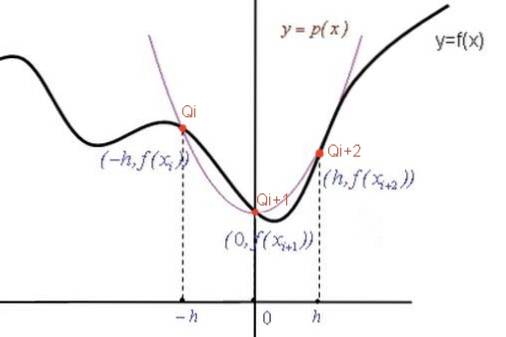
Para obter a fórmula de Simpson, em cada subintervalo [Xi, Xi + 2] a função f (X) é aproximada por um polinômio de segundo grau p (X) (parábola) que passa pelos três pontos: [Xi, f (Xi)] ; [Xi + 1, f (Xi + 1)] e [Xi + 2, f (Xi + 2)].
Em seguida, calculamos a integral do polinômio p (x) em [Xi, Xi + 2] que se aproxima da integral da função f (X) nesse intervalo.
Coeficientes do polinômio de interpolação
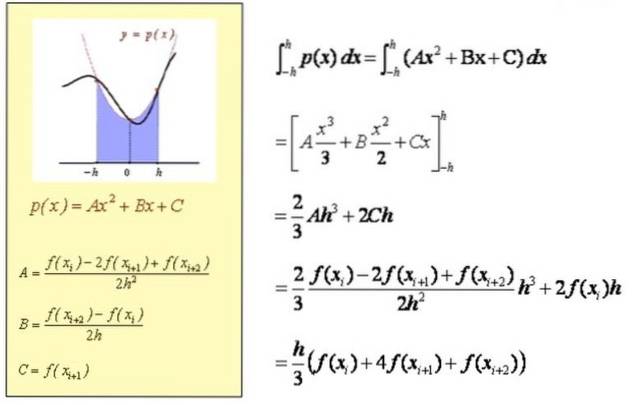
A equação da parábola p (X) tem a forma geral: p (X) = A Xdois + B X + C. Conforme a parábola passa pelos pontos Q indicados em vermelho (veja a figura), então os coeficientes A, B, C são determinados a partir do seguinte sistema de equações:
A (-h)dois - B h + C = f (Xi)
C = f (Xi + 1)
A (h)dois + B h + C = f (Xi + 2)
Pode-se ver que o coeficiente C é determinado. Para determinar o coeficiente A, adicionamos a primeira e a terceira equações obtendo:
2 A hdois + 2 C = f (Xi) + f (Xi + 2).
Em seguida, o valor de C é substituído e A é limpo, deixando:
A = [f (Xi) - 2 f (Xi + 1) + f (Xi + 2)] / (2 hdois)
Para determinar o coeficiente B, a terceira equação é subtraída da primeira e B é resolvida, obtendo:
B = [f (Xi + 2) - f (Xi)] = 2 h.
Em resumo, o polinômio de segundo grau p (X) que passa pelos pontos Qi, Qi + 1 e Qi + 2 tem coeficientes:
A = [f (Xi) - 2 f (Xi + 1) + f (Xi + 2)] / (2 hdois)
B = [f (Xi + 2) - f (Xi)] = 2 h
C = f (Xi + 1)
Cálculo da integral aproximada em [Xi, Xi + 2]
Cálculo aproximado da integral em [a, b]
Como já mencionado, no intervalo de integração total [a, b] uma partição é feita X0, X1, X2,…, Xn-1, Xn com a etapa h = Xi + 1 - Xi = (b - a) / n , onde n é um número par.
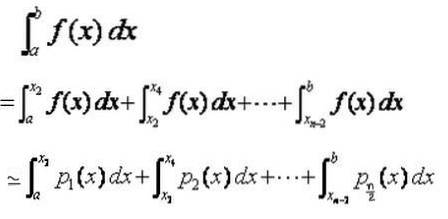
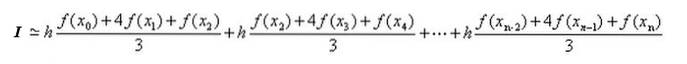
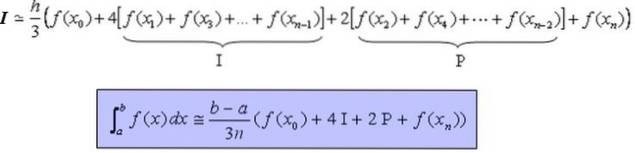
Erro de aproximação
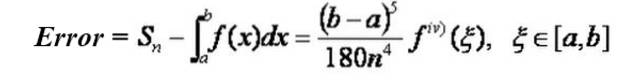
Observe que o erro diminui com a quarta potência do número de subdivisões no intervalo. Por exemplo, se você vai de n subdivisões para 2n, o erro diminui por um fator de 1/16.
O limite superior do erro obtido pela aproximação de Simpson pode ser obtido a partir desta mesma fórmula, substituindo a quarta derivada pelo valor máximo absoluto da quarta derivada no intervalo [a, b].
Exemplos trabalhados
- Exemplo 1
Considere a função a função f (X) = 1 / (1 + Xdois).
Encontre a integral definida da função f (X) no intervalo [-1, 1] usando o método de Simpson com duas subdivisões (n = 2).
Solução
Tomamos n = 2. Os limites de integração são a = -1 e b = -2, então a partição se parece com isto:
X0 = -1; X1 = 0 e X2 = +1.
Portanto, a fórmula de Simpson assume a seguinte forma:

Com n = 2 → xo = -1, x1 = 0; x2 = 1, portanto:

- Exemplo 2
Considere a função f (X) = 1 / (1 + Xdois).
Encontre a integral definida da função f (X) no intervalo [-1, 1] usando a fórmula de Simpson com quatro subdivisões (n = 4).
Solução
Tomamos n = 4. Os limites de integração são a = -1 e b = -2, então a partição se parece com isto:
X0 = -1; X1 = -1/2; X2 = 0; X3 = 1/2 e X4 = +1.
A fórmula de Simpson é declarada assim:
Integral ≃ [(b -a) / (3 n)] [f (X0) + 4 I + 2 P + f (Xn)]
Para o caso em que está sendo aplicado, é o seguinte:
Integral ≃ (1 - (1)) / (3⋅4)] [f (-1) + 4 [f (-½) + f (½)] + 2 [f (0)] + f (1)
Integral ≃ (2/12) [½ + 4 (⅘ + ⅘) + 2⋅1 + ½] = (⅙) [47/5] = 47/30 = 1,5666
- Exemplo 3
Determine a integral definida dos exemplos anteriores exatamente e faça uma comparação do resultado exato com aqueles obtidos usando a fórmula de Simpson nos exemplos 1a e 1b.
Solução
A integral indefinida da função f (X) = 1 / (1 + Xdois) é a função arctan (X).
Ao avaliar nos limites da integração permanece:
Integral = arctan (1) - arctan (-1) = π / 4 - (-π / 4) = π / 2 = 1,5708
Se compararmos o resultado da solução exata com o obtido pelo método de Simpson com n = 2 e n = 4, temos:
Para n = 2, a diferença entre a solução exata e a aproximada é π / 2 - 5/3 = -0,0959, ou seja, uma diferença percentual de -0,06%.
E para a aproximação de Simpson com n = 4, a diferença entre a solução exata e a aproximada é π / 2 - 47/30 = 0,0041, ou seja, uma diferença percentual de 0,003%.
Exercício proposto
O método de Simpson é adequado para ser aplicado em linguagens de programação e em aplicativos de computador para cálculos matemáticos. Sugere-se que o leitor, com base nas fórmulas apresentadas neste artigo, escreva seu próprio código em seu programa favorito.
A figura a seguir mostra um exercício no qual a fórmula de Simpson foi implementada em Estúdio Smath, software livre disponível para sistemas operacionais janelas Y Android.

Referências
- Casteleiro, J. M. 2002. Cálculo integral (edição ilustrada). Madrid: Editorial ESIC.
- UPV. Método de Simpson. Universidade politécnica de Valência. Recuperado de: youtube.com
- Purcell, E. 2007. Calculus Nona Edição. Prentice Hall.
- Wikipedia. Regra de Simpson. Recuperado de: es.wikipedia.com
- Wikipedia. Interpolação polinomial de Lagrange. Recuperado de: es.wikipedia.com



Ainda sem comentários