
Conceito de relações de proporcionalidade, exemplos e exercícios
As relações de proporcionalidade são ligações entre duas ou mais variáveis, de modo que, quando uma das quantidades varia, o mesmo ocorre com o valor das outras. Por exemplo, se um aumenta, os outros podem aumentar ou diminuir, mas em uma quantidade uniforme..
Os matemáticos da Grécia Antiga perceberam que algumas variáveis estavam relacionadas de uma maneira muito precisa. Eles perceberam que se um círculo tiver o dobro do diâmetro de outro, terá uma circunferência com o dobro do comprimento.

E se o diâmetro for triplicado, o contorno da circunferência também triplicará. Isso significa que um aumento no diâmetro produz um aumento proporcional no tamanho da circunferência..
E assim podemos afirmar que o comprimento da circunferência L é proporcional ao seu diâmetro D, que se expressa da seguinte forma:
L ∝ D
Onde o símbolo ∝ indica "diretamente proporcional a”. Para alterar o símbolo de proporcionalidade para o de igualdade e incorporar valores numéricos, é necessário determinar o vínculo entre as variáveis, denominado constante de proporcionalidade.
Depois de fazer muitas medições, os antigos matemáticos determinaram que a constante de proporcionalidade entre o tamanho L da circunferência e o diâmetro D da mesma era o número 3,1416 ... As elipses indicam um número infinito de casas decimais.
Este valor não é outro senão o famoso número π (pi) e desta forma escrevemos:
L = π.D
Desse modo, a relação entre o comprimento e o diâmetro de uma circunferência é igual à relação entre o comprimento e o diâmetro de outra. E o melhor é que agora temos uma maneira de calcular o comprimento de qualquer circunferência apenas sabendo seu diâmetro.
Índice do artigo
- 1 Exemplos de relações de proporcionalidade
- 2 Proporcionalidade direta e proporcionalidade inversa
- 3 Outros tipos de proporcionalidade
- 4 exercícios
- 4.1 - Exercício 1
- 4.2 - Exercício 2
- 5 referências
Exemplos de relações de proporcionalidade
Na ciência (e na vida cotidiana também) é muito importante encontrar relações entre variáveis, saber como as mudanças em uma afetam a outra. Por exemplo:
-Se você precisar de 3 xícaras de farinha para fazer uma dúzia de biscoitos. Quantas xícaras são necessárias para fazer 2 e meia dúzia?.
-Sabendo que um objeto no planeta Mercúrio pesa 4 vezes menos que na Terra, quanto pesará um carro de 1,5 tonelada em Mercúrio??
-Como a mudança na força aplicada afeta a aceleração do corpo no qual ela é aplicada??
-Se um veículo viaja com movimento retilíneo uniforme em uma rodovia e sabemos que ele percorre 30 km em 10 minutos, qual será a distância percorrida após 20 minutos?
-Quando temos um fio através do qual passa uma corrente elétrica, como a voltagem varia entre suas extremidades se aumenta?
-Se o diâmetro de um círculo for duplicado, como sua área é afetada??
-Como a distância afeta a intensidade do campo elétrico produzido por uma carga pontual?
A resposta está nas relações de proporcionalidade, mas nem todas as relações são do mesmo tipo. Então, nós os encontraremos para todas as situações levantadas aqui.
Proporcionalidade direta e proporcionalidade inversa
Duas variáveis x e y estão em proporção direta se estiverem relacionadas por:
y = kx
Onde k é a constante de proporcionalidade. Um exemplo é a relação entre as quantidades de farinha e biscoitos. Se representarmos graficamente essas variáveis, obtemos uma linha reta como a mostrada na figura:
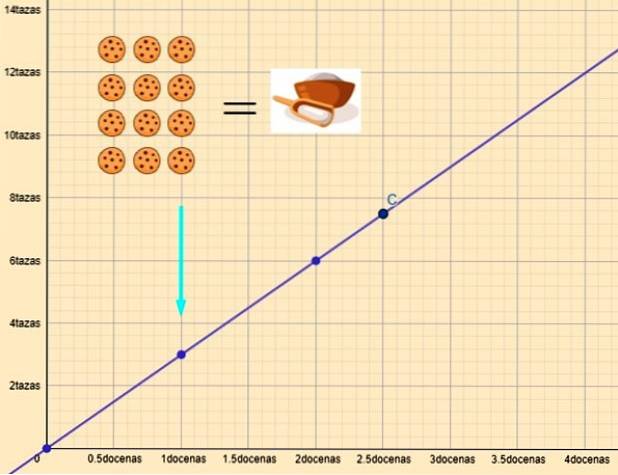
Se y são as xícaras de farinha e x são as dúzias de biscoitos, a relação entre eles é:
y = 3x
Para x = 1 dúzia, precisamos de y = 3 xícaras de farinha. E para x = 2,5 dúzias, y = 7,5 xícaras de farinha são necessárias.
Mas também temos:
-Aceleração para que um corpo experimenta é proporcional à força F agindo sobre ela, sendo a massa do corpo, chamada m, a constante de proporcionalidade:
F = mpara
Portanto, quanto maior for a força aplicada, maior será a aceleração produzida..
-Em condutores ôhmicos, a tensão V entre suas extremidades é proporcional à corrente I aplicada. A constante de proporcionalidade é a resistência R do condutor:
V = RI
-Quando um objeto se move com movimento retilíneo uniforme, a distância d é proporcional ao tempo t, sendo a velocidade v a constante de proporcionalidade:
d = v.t
Às vezes, encontramos duas quantidades tais que um aumento em uma produz uma diminuir proporcional no outro. Esta dependência é chamada razão inversa.
Por exemplo, na equação anterior, o tempo t necessário para percorrer uma certa distância d é inversamente proporcional à velocidade v da viagem:
t = d / v
E então enquanto mais alto é a velocidade v, menos tempo que o carro leva para percorrer a distância d. Se, por exemplo, a velocidade é duplicada, o tempo é reduzido pela metade.
Quando duas variáveis x e y estão em proporção inversa, podemos escrever:
y = k / x
Sendo k a constante de proporcionalidade. O gráfico dessa dependência é:
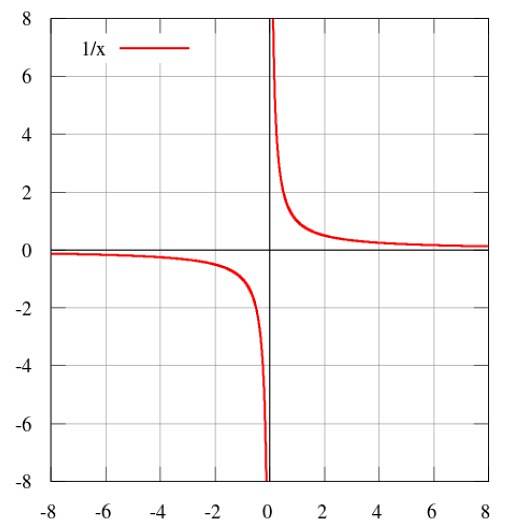
Outros tipos de proporcionalidade
Em um dos exemplos mencionados anteriormente, estávamos nos perguntando o que acontece com a área do círculo quando o raio aumenta. A resposta é que a área é diretamente proporcional ao quadrado do raio, onde π é a constante de proporcionalidade:
A = πRdois
Caso o raio seja dobrado, a área aumentará por um fator de 4.
E no caso do campo elétrico E produzido por uma carga pontual o que, sabe-se que a intensidade diminui com o inverso do quadrado da distância r para a carga o que:
E = ke q / rdois
Mas também podemos afirmar que a intensidade do campo é diretamente proporcional à magnitude da carga, sendo a constante de proporcionalidade ke, a constante eletrostática.
Outras proporcionalidades que também são apresentadas em Ciências são a proporcionalidade exponencial e a proporcionalidade logarítmica. No primeiro caso, as variáveis x e y são relacionadas por:
y = k.ax
Onde a é a base, um número positivo diferente de 0, que geralmente é 10 ou o número e. Por exemplo, o crescimento exponencial de bactérias tem esta forma.
No segundo caso, a relação entre as variáveis é:
y = k.logpara x
Novamente, a é a base do logaritmo, que geralmente é 10 (logaritmo decimal) ou e (logaritmo natural).
Treinamento
- Exercício 1
Sabendo que um objeto pesa 4 vezes menos no planeta Mercúrio do que na Terra, quanto pesaria um carro de 1,5 tonelada em Mercúrio??
Solução
Peso em Mercúrio = (1/4) Peso na Terra = (1/4) x 1,5 toneladas = 0,375 toneladas.
- Exercício 2
Para uma festa, alguns amigos decidem preparar suco de concentrado de frutas. As instruções da embalagem dizem que um copo de concentrado dá 15 copos de suco. Quanto concentrado é necessário para fazer 110 copos de suco?
Solução
Seja y o número de copos de suco ex o número de copos de concentrado. Eles são relacionados por:
y = kx
Substituindo os valores y = 15 e x = 1, a constante k é resolvida:
k = y / x = 15/1 = 15
Portanto:
110 = 15 x
x = 110/15 = 7,33 copos de concentrado de frutas.
Referências
- Baldor, A. 1974. Algebra. Cultural Venezolana S.A.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed Prentice Hall.
- Tutores do time do colégio. Relações de proporcionalidade. Recuperado de: varsitytutors.com
- Wikipedia. Proporcionalidade Recuperado de: es.wikipedia.org.
- Zill, D. 1984. Algebra and Trigonometry. Colina Mcgraw.


Ainda sem comentários