O relação matemática é o vínculo que existe entre os elementos de um subconjunto em relação ao produto de dois conjuntos. UMA Função envolve a operação matemática para determinar o valor de uma variável dependente com base no valor de uma variável independente. Cada função é uma relação, mas nem toda relação é uma função.
| Relação | Função | |
|---|---|---|
| Definição | Subconjunto de pares ordenados que correspondem ao produto cartesiano de dois conjuntos. | Operação matemática a ser realizada com a variável x para obter a variável Y. |
| Notação | x R Y; x está relacionado com Y. | Y= ƒ (x); Y é uma função de x. |
| Caracteristicas |
|
|
| Exemplos |
|
|
É chamada de relação binária de um conjunto A em um conjunto B ou a relação entre os elementos de A e B para cada subconjunto C do produto cartesiano A x B.
Ou seja, se o conjunto A é composto pelos elementos 1, 2 e 3, e o conjunto B é composto pelos elementos 4 e 5, o produto cartesiano de A x B será os pares ordenados:
A x B = (1,4), (2,4), (3, 4), (1,5), (2,5), (3,5).
O subconjunto C = (2,4), (3,5) será uma relação de A e B por ser composto pelos pares ordenados (2,4) e (3, 5), resultado do cartesiano produto de A x B.
"Sejam A e B quaisquer dois conjuntos não vazios, seja A x B o conjunto produto de ambos, ou seja: A x B é formado pelos pares ordenados (x, y) de modo que x é o elemento de A e Y é para B. Se qualquer subconjunto C é definido em A x B, uma relação binária em A e B é automaticamente determinada como segue:
x R Y se e somente se (x, y) ∈ C
(a notação x R Y Meios "x está relacionado com Y").
Vamos chamar de conjunto A conjunto inicial e vamos chamar o conjunto B conjunto de chegada.
O domínio de relacionamento são os elementos que compõem o conjunto inicial, enquanto o faixa de razão são os elementos do conjunto de chegada.
O conjunto PARA a partir de x elementos dos homens em uma população e B é o conjunto de Y elementos de mulheres da mesma população. Um relacionamento é estabelecido quando "x está casado com Y".
Quando falamos sobre uma função matemática de um conjunto A em um conjunto B, nos referimos a uma regra ou mecanismo que relaciona os elementos do conjunto A com um elemento do conjunto B.
"Sean x Y Y duas variáveis reais, diz-se então que y é uma função de x sim para cada valor que eu levo x corresponde a um valor de Y."
A variável independente é x enquanto que Y é a variável dependente ou função:
y = ƒ (x)
O conjunto no qual o x se denomina domínio da função (original) e a variação de Y gama de funções (foto).
O conjunto de pares (x, Y) de tal modo que Y= ƒ (x) se denomina gráfico de função; se são representados em eixos cartesianos, obtém-se uma família de pontos denominada gráfico de função.
Em matemática, temos muitos exemplos de funções. Aqui estão alguns exemplos de funções principais.
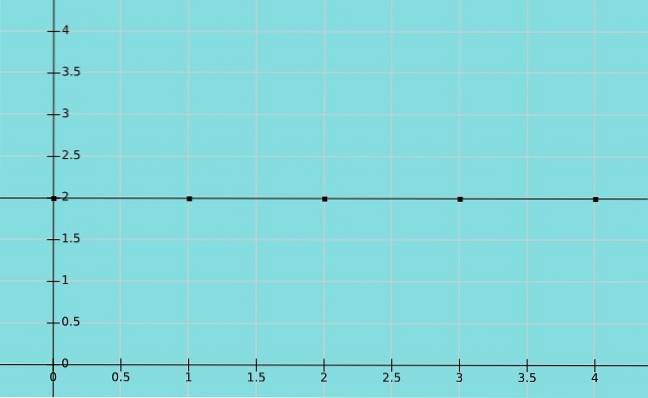
Uma função é chamada de constante se o elemento do conjunto B que corresponde ao conjunto A for o mesmo. Nesse caso, todos os valores de x correspondem ao mesmo valor de y. Assim, o domínio são os números reais, enquanto o intervalo é um valor constante.
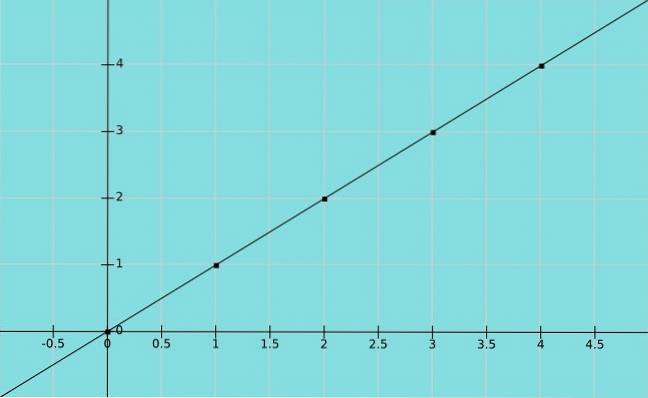
Vamos supor x é uma variável e isso Y tem o mesmo valor que x. Em seguida, temos uma função de identidade y = x, onde os paresx, y) no gráfico são (1,1), (2,2), (3,3) e assim por diante.
Uma função polinomial cumpre a forma y = anxn+paran-1+xn-1+… + Adoisxdois+para1x + a0. O gráfico acima mostra a função ƒ (x) = xdois+x-2.
Agora suponha que a variável dependente Y é igual à variável independente x elevado ao cubo. Temos a função y = x3, cujo gráfico é mostrado abaixo:
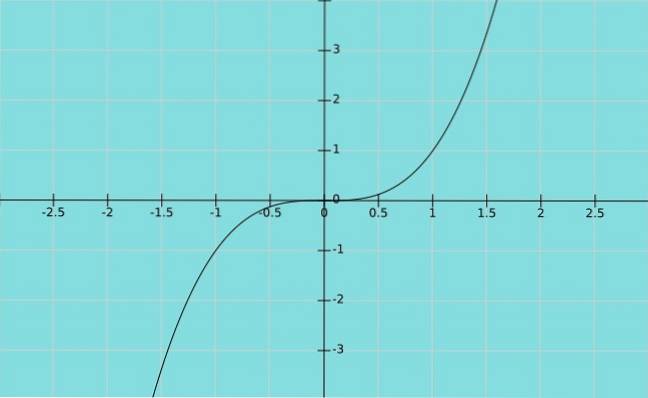
Ainda sem comentários