
Método gráfico de subtração de vetores, exemplos, exercícios
O subtração vetorial ou subtração vetorial entre vetores ou Y v denotado por ou - v, é calculado adicionando o vetor ou com o vetor oposto v. Algebricamente, a subtração é expressa da seguinte forma:
ou - v = ou + (-v)
É possível realizar a subtração vetorial seguindo vários procedimentos, por exemplo graficamente, desta forma um vetor v é desenhado por um segmento de linha orientado - uma seta-.
O comprimento da seta corresponde ao módulo do vetor, a inclinação - em relação a uma dada linha de referência - indica a direção e o final indica a direção do vetor.
O vetor oposto v tem o mesmo comprimento e direção, mas na direção oposta. Então, antes de fazer a subtração entre ou Y v, é necessário desenhar o vetor oposto v, e adicionar este vetor a você.
É muito importante observar que a subtração vetorial não é comutativa, ou seja, a ordem dos vetores altera o resultado, portanto:
ou - v ≠ v - ou
O procedimento gráfico pode ser realizado por qualquer um destes métodos, cujos passos explicaremos a seguir:
-Método Triângulo.
-Método de paralelogramo.
Índice do artigo
- 1 Método gráfico de subtração vetorial
- 1.1 Método do triângulo
- 1.2 Método de paralelogramo
- 2 Exemplos de subtração vetorial
- 2.1 - Exemplo 1
- 2.2 - Exemplo 2
- 3 Exercício resolvido
- 3.1 Solução
- 4 referências
Método de subtração de vetor gráfico
Método Triângulo
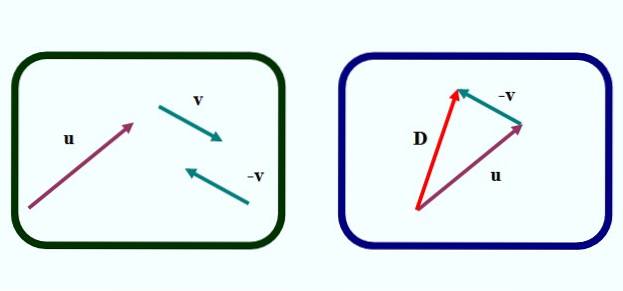
Na figura 1, temos o primeiro dos métodos para subtrair graficamente dois vetores. É sobre método do triângulo, porque a figura que se forma pelo estabelecimento dos vetores é um triângulo, como podemos ver na imagem à esquerda.
Para fazer a subtração ou - v procedemos da seguinte forma:
-Desenhe o vetor -v do vetor v, por translação com uma régua e um quadrado, mas mudando a direção da seta (imagem à esquerda).
-Move para o vetor -v de forma que sua origem coincida com o final do vetor ou (imagem certa).
-Em seguida, é desenhado um vetor (em vermelho na imagem da direita) que vai da origem de ou até o fim de v. Ligar D y é o vetor de diferença:
D = ou - v
Método de paralelogramo
No método do paralelogramo, os vetores a serem somados ou subtraídos devem coincidir em seus pontos de origem. Suponha que queremos encontrar ou - v Com nossos vetores mostrados acima, as etapas para encontrar a subtração de vetores por este método são as seguintes:
-Determine o vetor oposto v, o que é -v, como descrito acima para o método do triângulo.
-Traduzir vetores cuidadosamente ou Y -v de tal forma que suas origens coincidam.
-Agora, linhas paralelas segmentadas são desenhadas a partir das extremidades de cada vetor. A figura que se forma é um paralelogramo e, em casos especiais em que os vetores são perpendiculares, resulta um retângulo ou um quadrado..
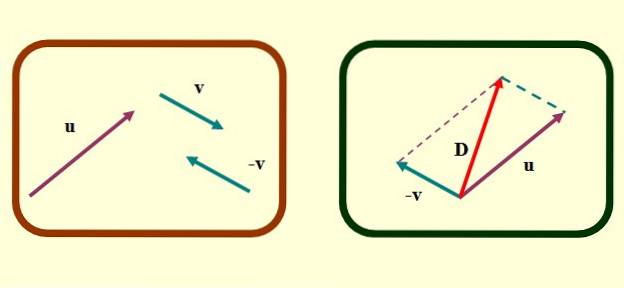
-Finalmente, é desenhado um vetor que começa na origem comum de ou Y v ao extremo onde as linhas paralelas segmentadas se cruzam. Este é o vetor D ou subtração.
Importante
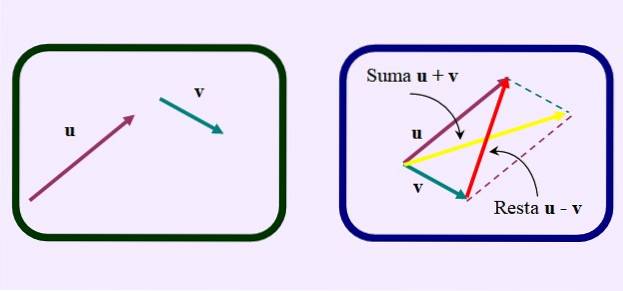
Outra forma de fazer a subtraçãoé desenhar o paralelogramo como se quisesse adicionar os vetores.
Mas em vez de desenhar a diagonal usual da soma, que vai da origem comum até a intersecção dos paralelos, o diagonal oposta ou mais curta, como pode ser visto na figura:
Exemplos de subtração vetorial
- Exemplo 1
Um navio navega em um rio e o faz na direção oposta à corrente. Um observador em terra observa que a velocidade do barco é reduzida devido à ação da corrente.
A velocidade é um vetor e neste exemplo, a velocidade do barco está apontando em uma direção e a velocidade da corrente tem a mesma direção e direção oposta. A velocidade líquida do navio é a soma de ambos os vetores.
Por exemplo, se os instrumentos do barco indicam que está se movendo a v '= + 40 km / he um observador na costa mede que o barco está se movendo a v = + 30 km / h. Já que v = v '+ Vc, onde Vc é a velocidade da corrente que é calculada subtraindo as velocidades v e v' respectivamente: Vc = v - v '= 30 km / h - 40 km / h = -10 km / h.
- Exemplo 2
Na cinemática, temos vetores importantes que descrevem mudanças:
-Compensação para mudanças de posição.
-Velocidade média, para quantificar o quão rápido a posição varia ao longo do tempo.
-Aceleração, para mudanças de velocidade em função do tempo.
O vetor de deslocamento
O vetor de deslocamento descreve a mudança de posição que um corpo experimenta durante seu movimento.
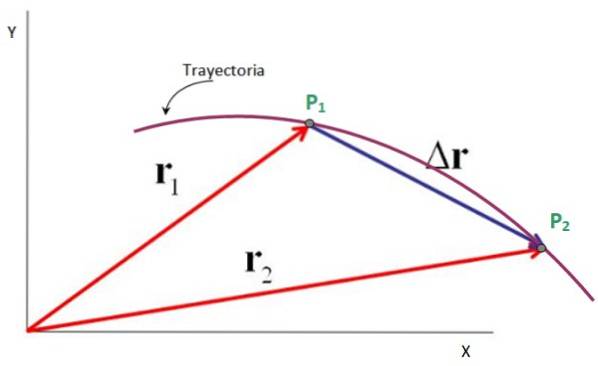
Vejamos, por exemplo, uma partícula que descreve a trajetória plana mostrada na figura, na qual passa do ponto P1 apontar Pdois.
Os vetores direcionados da origem do sistema de coordenadas x-y para esses pontos são os vetores de posição r1 Y rdois, enquanto o vetor de deslocamento é Δr, isso vai de P1 principaldois. É verdade que:
Δr = rdois - r1
Portanto, o vetor deslocamento é a subtração entre o vetor posição final e o vetor posição inicial, conforme mostrado na figura a seguir. Suas unidades também são as de posição: metros, pés, milhas, centímetros e muito mais..
Os vetores de velocidade média e aceleração média
Por sua vez, o vetor de velocidade média vm é definido como o deslocamento multiplicado pelo inverso do intervalo de tempo:


Exercício resolvido
Uma partícula que descreve um círculo leva 5 s para passar do ponto A ao ponto B. Em A ela tem uma velocidade vPARA = 60 km / h em direção ao eixo + x e em B é vB = 60 km / h em direção a + y. Determine sua aceleração média de forma gráfica e analítica.
Solução
Na forma gráfica, a direção e a direção da aceleração média são determinadas por:

Na imagem a seguir está a subtração vB - vPARA, usando o método do triângulo, uma vez que a aceleração média param é proporcional a Δv. O triângulo formado tem as duas pernas iguais e, portanto, os ângulos internos agudos medem 45º cada..

Analiticamente, se a direção + x coincide com o vetor unitário eu e a direção + y com o vetor unitário j, então:
Δv = 60 km / h j - 60 km / h eu
Tomando Δt = 5 s, de acordo com as informações do enunciado, a aceleração média é:
param = (60 km / h j - 60 km / h eu) / 5 s = 12 (j-eu) km / (h.s)
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison wesley.
- Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Física. 2ª Ed. McGraw Hill.
- Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 1.
- Tipler, P. 2006. Física para Ciência e Tecnologia. 5ª Ed. Volume 1. Editorial Reverté.



Ainda sem comentários