
Explicação da segunda condição de equilíbrio, exemplos, exercícios
O segunda condição de equilíbrio estabelece que a soma dos torques ou momentos produzidos por todas as forças atuantes sobre um corpo, independentemente do ponto em que sejam calculadas, deve ser cancelada para que o referido corpo fique em equilíbrio estático ou dinâmico.
Denotando o torque ou momento de força pela letra grega τ, matematicamente, é expresso assim:
∑ τ = 0

A letra em negrito indica a natureza vetorial do momento, que deve ser cancelada em relação a qualquer ponto escolhido como centro de rotação. Dessa forma, o cancelamento do torque líquido garante que o objeto não comece a girar ou tombar..
No entanto, se o objeto já estava girando anteriormente e o torque líquido desaparecer repentinamente, a rotação continuará, mas com velocidade angular constante.
A segunda condição de equilíbrio é usada em conjunto com a primeira condição, que diz que a soma das forças em um corpo deve ser zero, para que não se traduza, ou que se o fizer, é com movimento retilíneo uniforme:
∑ F = 0
Ambas as condições se aplicam a corpos estendidos, aqueles cujas dimensões são mensuráveis. Quando um objeto é considerado uma partícula, não faz sentido falar de rotações, e a primeira condição é suficiente para garantir o equilíbrio.
Exemplos
A segunda condição de equilíbrio é revelada em inúmeras situações:
Enquanto você sobe a escada
Ao apoiar uma escada no chão e na parede, precisamos de atrito suficiente, especialmente no chão, para garantir que a escada não escorregue. Se tentarmos subir em uma escada apoiada em um piso oleoso, úmido ou escorregadio, não é difícil antecipar que iremos cair.
Para poder usar a escada com confiança, é necessário que ela esteja em equilíbrio estático ao subir e quando estiver no degrau exigido.
Movendo um armário
Quando você deseja mover um móvel alto, como um armário, ou qualquer peça cuja altura seja maior que a largura, é conveniente empurrar em um ponto baixo, para evitar tombar, desta forma é mais provável que o a mobília deslizará em vez de girar e se deitará.
Nessas circunstâncias, a mobília não está necessariamente em equilíbrio, pois poderia se mover rapidamente, mas pelo menos não tombaria.
Varandas
As varandas que se projetam dos edifícios devem ser construídas garantindo que, mesmo que haja muitas pessoas no topo, não tombe e desmorone.
Dielétricos em campos elétricos externos
Ao colocar um material dielétrico em um campo elétrico externo, as moléculas se movem e giram até adotar uma posição de equilíbrio, criando um campo elétrico dentro do material..
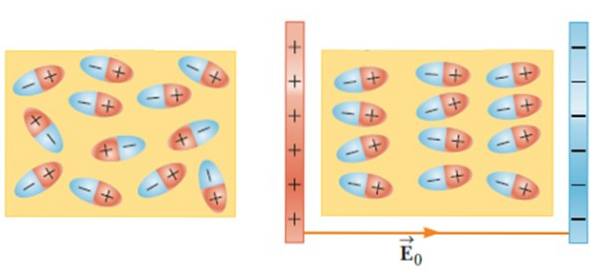
Este efeito aumenta a capacidade de um capacitor quando um material como vidro, borracha, papel ou óleo é inserido entre suas armações..
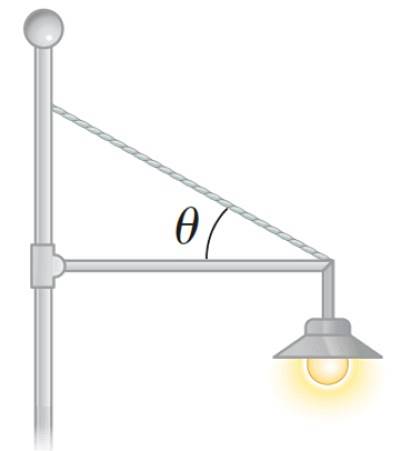
Letreiros e lâmpadas
É comum que muitos moradores pendurem avisos na parede do prédio, de modo que fiquem visíveis aos transeuntes.
O pôster é sustentado por uma barra e um cabo, ambos fixados na parede por suportes. As várias forças que atuam devem garantir que o cartaz não caia, para o que as duas condições de equilíbrio entram em jogo.
Um refletor também pode ser colocado desta forma em um parque, como na figura a seguir:
Como calcular o torque líquido ou o momento líquido de uma força?
O torque ou momento de uma força, denotado por τ ou M em alguns textos, é sempre calculado em relação a algum ponto por onde passa o eixo de rotação.
É definido como o produto vetorial entre o vetor posição r, que é direcionado do referido eixo para o ponto de aplicação da força e a força F:
τ = r × F
Sendo um vetor, é necessário expressar o torque dando sua magnitude, direção e sentido. A magnitude é dada por:
τ = rF.sen θ
Regra da mão direita para produto vetorial
Quando o problema está no plano, a direção do torque é perpendicular ao papel ou tela, e a direção é determinada pela regra da mão direita, na qual o dedo indicador aponta para r, dedo médio em direção F e o polegar aponta para dentro ou para fora do papel.
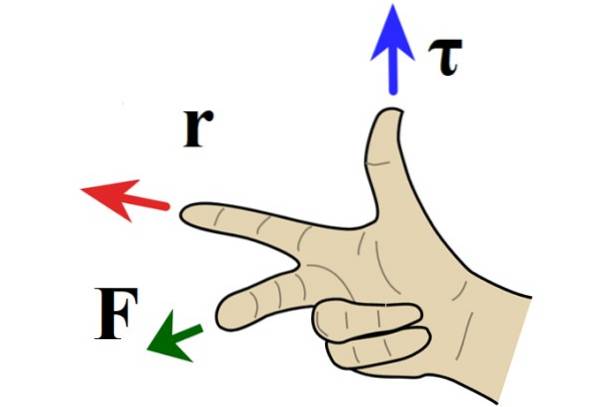
Quando o torque aponta para fora do papel, a rotação é no sentido anti-horário e recebe um sinal positivo por convenção. Se, em vez disso, o torque for direcionado para o interior da lâmina, a rotação é no sentido horário e negativa..
Para encontrar o torque líquido, é escolhido um ponto conveniente para o cálculo, que pode ser aquele em que atua a maior quantidade de forças. Neste caso o momento dessas forças é zero, pois possui um vetor posição r de magnitude 0.
Você pode escolher qualquer ponto que ofereça informações suficientes para resolver o desconhecido que pede a solução do problema. Vamos ver com mais detalhes abaixo.
Exercício resolvido
O refletor da figura a seguir tem massa de 20 kg e é sustentado por uma fina barra horizontal, de massa desprezível e comprimento L, que é articulada a um poste. O cabo, também leve, que ajuda a sustentar o refletor forma um ângulo θ = 30º com a barra. Calcular:
a) A tensão no cabo
b) A magnitude da força F que o poste exerce na barra através da dobradiça.
Solução
Vamos aplicar a primeira condição de equilíbrio ∑ F = 0 às forças mostradas no diagrama:
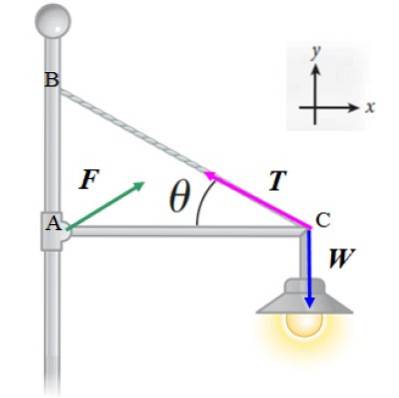
F + T + W = 0
Observe que a magnitude e a direção de F ainda não foram determinados, mas assumimos que tem dois componentes: Fx e FY. Desta forma, obtemos duas equações:
Fx -T. cos θ = 0
FY - W + T⋅ sen θ = 0
Agora vamos aplicar a segunda condição de equilíbrio, escolhendo o ponto A, uma vez que não sabemos a magnitude de F nem aquele de T. Ao escolher este ponto, o vetor rPARA é nulo, portanto, o momento de F é nulo e a magnitude de F não aparecerá na equação:
-W⋅L + T⋅sen θ⋅L = 0
Portanto:
T.sen θ.L = W.L
T = W / sin θ = (20 kg x 9,8 m / sdois) / Sin 30º = 392 N
Sabendo a magnitude de T, podemos resolver para o componente Fx:
Fx = T⋅ cos θ = 392 cos 30º N = 339. 5 N
E então o componente FY:
FY = W - T⋅ sen θ = (20 kg x 9,8 m / sdois) - 392⋅sin 30º = 0
Então podemos expressar F Então:
F = 339,5 N x
Portanto, é uma força horizontal. Isso ocorre porque consideramos que a barra tinha peso insignificante.
Se o ponto C tivesse sido escolhido para calcular o momento resultante, os vetores rT Y rC são nulos, portanto:
M = FeL = 0
Conclui-se que FY = 0. Desta forma:
- W + T⋅ sen θ = 0
T = W / sin θ
Que é o mesmo resultado obtido inicialmente ao escolher o ponto A como o local por onde passa o eixo de rotação.
Assuntos de interesse
Condições de equilíbrio.
Primeira condição de equilíbrio.
Referências
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison wesley.
- Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 4. Sistemas de partículas. Editado por Douglas Figueroa (USB).
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed Prentice Hall.
- Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 1.
- Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 1. 7º. Ed. Cengage Learning.

Ainda sem comentários