
Segunda lei da termodinâmica, fórmulas, equações, exemplos
O Segunda lei da termodinâmica tem várias formas de expressão. Um deles afirma que nenhuma máquina de calor é capaz de converter completamente toda a energia que absorve em trabalho utilizável (formulação de Kelvin-Planck). Outra forma de afirmar isso é dizer que processos reais ocorrem de tal forma que a qualidade da energia é inferior porque o entropia tende a aumentar.
Essa lei, também conhecida como o segundo princípio da termodinâmica, tem se expressado de diferentes maneiras ao longo do tempo, desde o início do século 19 até os dias atuais, embora suas origens datem da criação das primeiras máquinas a vapor na Inglaterra, no início de o século 18.

Mas embora se expresse de várias formas, a ideia de que a matéria tende a se desordenar e de que nenhum processo é 100% eficiente, pois sempre haverá perdas..
Todos os sistemas termodinâmicos aderem a esse princípio, desde o próprio universo até a xícara de café da manhã que espera calmamente na mesa trocando calor com o meio ambiente..
O café esfria com o passar do tempo, até que esteja em equilíbrio térmico com o meio ambiente, por isso seria muito surpreendente se um dia acontecesse o contrário e o ambiente esfriasse enquanto o café se aquecia. É improvável que aconteça, alguns dirão impossível, mas imagine só para ter uma ideia do sentido em que as coisas acontecem espontaneamente.
Em outro exemplo, se deslizarmos um livro sobre a superfície de uma mesa, ele acabará parando, porque sua energia cinética será perdida na forma de calor devido ao atrito..
A primeira e a segunda leis da termodinâmica foram estabelecidas por volta de 1850, graças a cientistas como Lord Kelvin - criador do termo "termodinâmica" -, William Rankine - autor do primeiro texto formal sobre termodinâmica - e Rudolph Clausius..
Índice do artigo
- 1 Fórmulas e equações
- 1.1 Processos reversíveis e irreversíveis
- 2 inscrições
- 2.1 Motor Carnot
- 2.2 Metabolismo humano
- 3 exemplos
- 4 exercícios resolvidos
- 4.1 Exercício 1
- 4.2 Exercício 2
- 4.3 Exercício 3
- 5 referências
Fórmulas e equações
A entropia - mencionada no início - nos ajuda a estabelecer o sentido em que as coisas acontecem. Voltemos ao exemplo de corpos em contato térmico.
Quando dois objetos em temperaturas diferentes entram em contato e, finalmente, depois de um tempo atingem o equilíbrio térmico, eles são levados a isso pelo fato de que a entropia atinge seu máximo, quando a temperatura de ambos é a mesma.
Denotando entropia como S, a mudança na entropia ΔS de um sistema é dado por:

A mudança de entropia ΔS indica o grau de desordem de um sistema, mas há uma restrição no uso desta equação: ela é aplicável apenas a processos reversíveis, ou seja, aqueles em que o sistema pode retornar ao seu estado original sem deixar vestígios do ocorrido-.
Em processos irreversíveis, a segunda lei da termodinâmica aparece assim:

Processos reversíveis e irreversíveis
A xícara de café sempre esfria e é um bom exemplo de processo irreversível, pois sempre ocorre em apenas uma direção. Se adicionar creme ao café e batê-lo obterá uma combinação muito agradável, mas por mais que volte a bater, não terá o café e o creme à parte, porque mexer é irreversível..

Embora a maioria dos processos diários sejam irreversíveis, alguns são quase reversível. A reversibilidade é uma idealização. Para que isso aconteça, o sistema deve mudar muito lentamente, de forma que a cada ponto esteja sempre em equilíbrio. Desta forma, é possível devolvê-lo a um estado anterior sem deixar vestígios nas redondezas..
Processos que se aproximam desse ideal são mais eficientes, pois entregam uma maior quantidade de trabalho com menor consumo de energia..
A força de atrito é responsável por grande parte da irreversibilidade, pois o calor gerado por ela não é o tipo de energia que se busca. No livro deslizando pela mesa, o calor de fricção é a energia que não é recuperada.
Embora o livro volte à sua posição original, a mesa estará quente como um vestígio de idas e vindas sobre ela.
Agora olhe para uma lâmpada incandescente: a maior parte do trabalho feito pela corrente através do filamento é desperdiçada no calor pelo efeito Joule. Apenas uma pequena porcentagem é usada para emitir luz. Em ambos os processos (livro e lâmpada), a entropia do sistema aumentou.
Formulários
Um motor ideal é aquele que é construído usando processos reversíveis e sem atrito que causa desperdício de energia, convertendo quase toda a energia térmica em trabalho utilizável.
Ressaltamos a palavra quase, porque mesmo o motor ideal, que é o de Carnot, não é 100% eficiente. A segunda lei da termodinâmica garante que este não seja o caso.
Motor Carnot
O motor Carnot é o motor mais eficiente que pode ser criado. Opera entre dois tanques de temperatura em dois processos isotérmicos - a temperatura constante - e dois processos adiabáticos - sem transferência de energia térmica-.
Os gráficos chamados diagramas de PV -pressão-volume- esclarecem a situação em um relance:
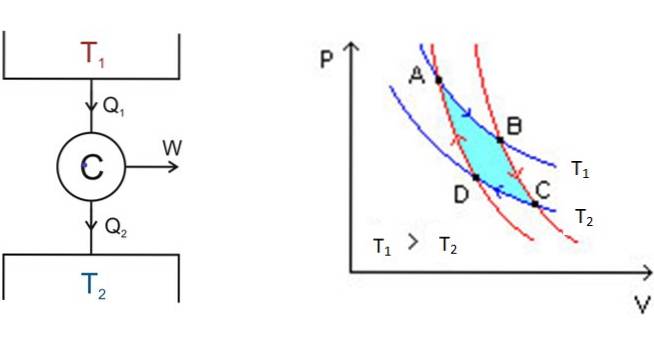
À esquerda, na figura 3 está o diagrama do motor C de Carnot, que leva calor Q1 do tanque que está na temperatura T1, converte esse calor em trabalho W e produz os resíduos Qdois para o tanque mais frio, que está na temperatura Tdois.
A partir de A, o sistema se expande até chegar a B, absorvendo calor na temperatura fixa T1. Em B, o sistema inicia uma expansão adiabática em que nenhum calor é ganho ou perdido, para atingir C.
Em C, outro processo isotérmico começa: o de transferência de calor para o outro depósito térmico mais frio que está em Tdois. À medida que isso acontece, o sistema é comprimido e atinge o ponto D. Começa um segundo processo adiabático para retornar ao ponto inicial A. Desta forma, um ciclo é concluído.
A eficiência do motor Carnot depende das temperaturas em kelvins dos dois reservatórios térmicos:
Eficiência máxima = (Qentrada - Qsaída) / Qentrada = 1 - (Tdois/ T1)
O teorema de Carnot afirma que este é o motor térmico mais eficiente que existe, mas não se apresse em comprá-lo. Lembra do que falamos sobre a reversibilidade do processo? Eles têm que acontecer muito, muito lentamente, então a potência de saída desta máquina é praticamente zero..
Metabolismo humano
O ser humano precisa de energia para manter todos os seus sistemas funcionando, por isso se comportam como máquinas térmicas que recebem energia e a transformam em energia mecânica para, por exemplo, se movimentar..
Eficiência e do corpo humano durante o trabalho pode ser definido como o quociente entre a potência mecânica que ele pode fornecer e a entrada de energia total, que vem com os alimentos.
Como a potência média Pm é o trabalho W feito em um intervalo de tempo Δt, pode ser expresso como:
Pm = W / Δt
sim ΔU / Δt é a taxa em que a energia é adicionada, a eficiência do corpo é como:
Por meio de vários testes com voluntários, eficiências de até 17% foram obtidas, fornecendo cerca de 100 watts de energia por várias horas.
Claro, isso dependerá em grande parte da tarefa realizada. Pedalar uma bicicleta é um pouco mais eficiente, cerca de 19%, enquanto as tarefas repetitivas que incluem pás, picaretas e enxadas chegam a 3%..
Exemplos
A segunda lei da termodinâmica está implícita em todos os processos que ocorrem no Universo. A entropia está sempre aumentando, embora em alguns sistemas pareça estar diminuindo. Para que isso aconteça teve que aumentar em outro lugar, de modo que no saldo total seja positivo.
- Na aprendizagem, há entropia. Existem pessoas que aprendem bem e com rapidez, além de poderem se lembrar facilmente depois. Diz-se que são pessoas com baixo aprendizado de entropia, mas certamente são menos numerosos do que aqueles com alta entropia: aqueles que têm mais dificuldade de se lembrar das coisas que estudam..
- Uma empresa com trabalhadores desorganizados tem mais entropia do que outra em que os trabalhadores realizam as tarefas de maneira ordenada. É claro que este último será mais eficiente do que o anterior.
- As forças de atrito geram menos eficiência na operação das máquinas, pois aumentam a quantidade de energia dissipada que não pode ser utilizada de forma eficiente.
- Jogar um dado tem uma entropia mais alta do que jogar uma moeda. Afinal, jogar uma moeda tem apenas 2 resultados possíveis, enquanto jogar o dado tem 6. Quanto mais eventos forem prováveis, maior será a entropia..
Exercícios resolvidos
Exercício 1
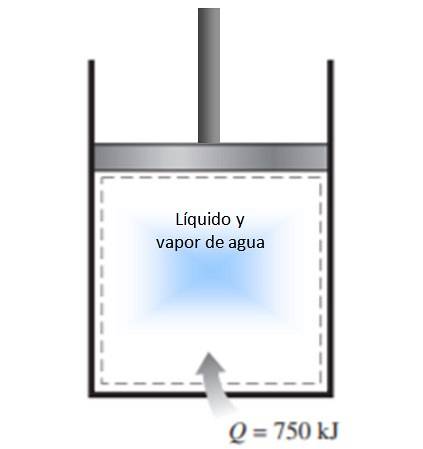
Um cilindro de pistão é preenchido com uma mistura de líquido e vapor d'água a 300 K e 750 kJ de calor é transferido para a água por um processo de pressão constante. Como resultado, o líquido dentro do cilindro vaporiza. Calcule a mudança na entropia no processo.

Solução
O processo descrito no comunicado é realizado a pressão constante em sistema fechado, que não sofre troca de massa..
Por se tratar de uma vaporização, durante a qual a temperatura também não muda (durante as mudanças de fase a temperatura é constante), a definição de mudança de entropia dada acima pode ser aplicada e a temperatura pode sair do integral:
ΔS = 750.000 J / 300 K = 2500 J / K.
Uma vez que o calor entra no sistema, a mudança na entropia é positiva.
Exercício 2
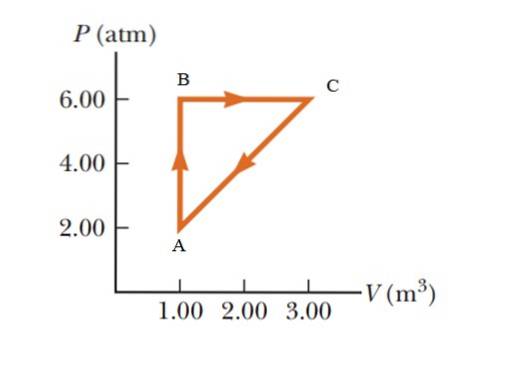
Um gás sofre um aumento de pressão de 2,00 para 6,00 atmosferas (atm), mantendo um volume constante de 1,00 m3, e então expandir a pressão constante até atingir um volume de 3,00 m3. Finalmente, ele retorna ao seu estado inicial. Calcule quanto trabalho é feito em 1 ciclo.

Solução
É um processo cíclico no qual a variação da energia interna é zero, de acordo com a primeira lei da termodinâmica, portanto Q = W. Em um diagrama PV (pressão - volume), o trabalho realizado durante um processo cíclico é igual à área delimitada por a curva. Para dar os resultados no Sistema Internacional, é necessário fazer uma mudança de unidade na pressão usando o seguinte fator de conversão:
1 atm = 101,325 kPa = 101,325 Pa.
A área delimitada pelo gráfico corresponde à de um triângulo cuja base (3 - 1 m3) = 2 m3 e cuja altura é (6 - 2 atm) = 4 atm = 405.300 Pa
CABCA = ½ (2 m3 x 405300 Pa) = 405300 J = 405,3 kJ.
Exercício 3
Diz-se que uma das máquinas mais eficientes já construídas é uma turbina a vapor movida a carvão no rio Ohio, que é usada para alimentar um gerador elétrico operando entre 1870 e 430 ° C..
Calcule: a) A eficiência teórica máxima, b) A potência mecânica entregue pela máquina se esta absorver 1,40 x 105 J de energia a cada segundo do tanque quente. A eficiência real é conhecida como 42,0%.
Solução
a) A eficiência máxima é calculada com a equação dada acima:
Eficiência máxima = (Qentrada - Q saída) / Qentrada = 1 - (Tdois/ T1)
Para alterar os graus centígrados para Kelvin, basta adicionar 273,15 à temperatura centígrada:

Multiplicar por 100% dá a eficiência percentual máxima, que é 67,2%
c) Se a eficiência real é de 42%, há uma eficiência máxima de 0,42.
A potência mecânica fornecida é: P = 0,42 x 1,40 x10 5 J / s = 58800 W.
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill.
- Cengel, Y. 2012. Thermodynamics. 7mãe Edição. Colina Mcgraw.
- Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 4. Fluidos e termodinâmica. Editado por Douglas Figueroa (USB).
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach.
- López, C. A Primeira Lei da Termodinâmica. Recuperado de: culturacientifica.com.
- Serway, R. 2011. Fundamentals of Physics. 9n / D Cengage Learning.
- Sevilla University. Máquinas Térmicas. Recuperado de: laplace.us.es



Ainda sem comentários