
Aplicações, experimentos e exercícios da segunda lei de Newton
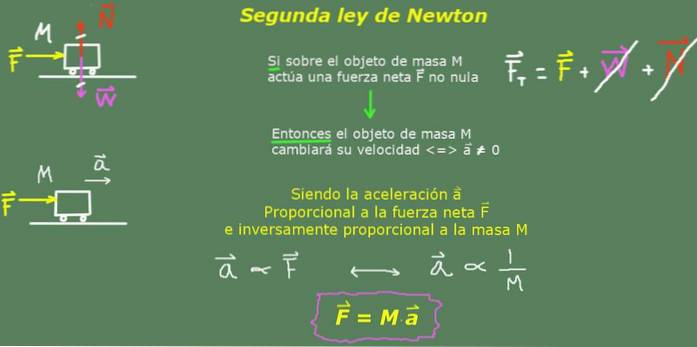
O segunda lei de newton ou a lei fundamental da dinâmica estabelece que se um objeto é submetido a uma força ou a um conjunto de forças que não se cancelam, então o objeto irá acelerar na direção da força resultante, sendo esta aceleração proporcional à intensidade dessa força resultante e inversamente proporcional à massa do objeto.
sim F é a força líquida, M a massa do objeto e para a aceleração que adquire, então a segunda lei de Newton seria expressa matematicamente assim: para = F / M ou da maneira mais usual F = M∙para
Índice do artigo
- 1 Explicação e fórmulas
- 2 exercícios resolvidos
- 2.1 Exercício 1
- 2.2 Exercício 2
- 3 aplicações da segunda lei de Newton
- 3.1 A aceleração de um elevador
- 3.2 O pote de maionese
- 4 experimentos para crianças
- 4.1 Experimento 1
- 4.2 Experimento 2
- 5 artigos de interesse
- 6 referências
Explicação e fórmulas
Conforme explicado acima, a maneira usual de expressar a segunda lei é com a fórmula:
F = M∙para
Tanto a aceleração quanto a força devem ser medidas a partir de um referencial inercial. Observe que a massa é uma quantidade positiva, então a aceleração aponta na mesma direção da força resultante.
Observe também que quando a força resultante é zero (F = 0) então a aceleração também será zero ( para = 0 ) sempre que M> 0. Este resultado está totalmente de acordo com a primeira lei de Newton ou lei da inércia.
A primeira lei de Newton estabelece sistemas de referência inerciais como aqueles que se movem com velocidade constante em relação a uma partícula livre. Na prática e para os fins das aplicações mais comuns, um sistema de referência fixo ao solo ou qualquer outro que se mova a uma velocidade constante em relação a ele, será considerado inercial..
Força é a expressão matemática da interação do objeto com o meio ambiente. A força pode ser uma quantidade constante ou mudar com o tempo, a posição e a velocidade do objeto..
A unidade no Sistema Internacional (SI) para força é o Newton (N). A massa no (SI) é medida em (kg) e a aceleração em (m / sdois) Um Newton de força é a força necessária para acelerar um objeto de massa 1 kg a 1 m / sdois .
Exercícios resolvidos
Exercício 1
Um objeto de massa m é liberado de uma certa altura e uma aceleração de queda de 9,8 m / s² é medida.
O mesmo acontece com outro objeto de massa m 'e outro de massa m "e outro e outro. O resultado é sempre a aceleração da gravidade que é denotada por ge é igual a 9,8 m / s². Nestes experimentos a forma do objeto e o valor de sua massa é tal que a força devida à resistência do ar é desprezível.
Ele é solicitado a encontrar um modelo para a força atrativa da terra (conhecido como peso) que seja consistente com os resultados experimentais..
Solução
Escolhemos um sistema de referência inercial (fixo em relação ao solo) com uma direção positiva do eixo vertical X e para baixo.
A única força agindo sobre o objeto de massa m é a atração da terra, essa força é chamada de peso P, como aponta para baixo é positivo.
A aceleração que o objeto de massa adquire m uma vez que é lançado é a = g , apontado para baixo e positivo.
Propomos a segunda lei de Newton
P = m a
Qual será o modelo de P tal que a aceleração prevista pela segunda lei seja g independentemente do valor de m? : A única alternativa é que P = m g sempre que m> 0.
m g = m a de onde saímos: a = g
Concluímos que o peso, a força com que a Terra atrai um objeto será a massa do objeto multiplicada pela aceleração da gravidade e sua direção é vertical e apontada para baixo..
P = m∙g
Exercício 2
Um bloco de 2 kg de massa repousa sobre um piso totalmente plano e horizontal. Se uma força de 1 N é aplicada a ele, qual é a aceleração do bloco e que velocidade ele terá após 1 s.
Solução
A primeira coisa é definir um sistema de coordenadas inercial. Um foi escolhido com o eixo X no chão e o eixo Y perpendicular a ele. Em seguida, é feito um diagrama de forças, colocando as forças devidas às interações do bloco com seu ambiente.

A força N representa a normal, é a força vertical para cima que a superfície do piso exerce sobre o bloco M. Sabe-se que N equilibra exatamente P porque o bloco não se move na direção vertical.
F é a força horizontal aplicada ao bloco M, apontando na direção positiva do eixo X.
A força resultante é a soma de todas as forças no bloco de massa M. Fazemos a soma vetorial de F, P e N. Como P e N são iguais e opostos, eles se cancelam, e a força resultante é F.
Portanto, a aceleração resultante será o quociente entre a força resultante e a massa:
a = F / M = 1 N / 2 kg = 0,5 m / s²
Como o bloco começa do repouso após 1s, sua velocidade terá mudado de 0 m / s para 0,5 m / s .
Aplicações da Segunda Lei de Newton
Acelerando um elevador
Um menino usa uma balança de banheiro para medir seu peso. O valor que você obtém é 50 kg. Em seguida, o menino leva o peso para o elevador de seu prédio, pois quer medir a aceleração do elevador. Os resultados obtidos na inicialização são:
- A balança registra um peso de 58 kg por 1,5 s
- Em seguida, meça 50 kg novamente.
Com esses dados, calcule a aceleração do elevador e a velocidade que ele adquire.
Solução
A balança mede o peso em uma unidade chamada kilogram_force. Por definição, kilogram_force é a força com a qual o planeta Terra atrai um objeto de massa 1 kg.
Quando a única força que atua sobre o objeto é o seu peso, ele adquire uma aceleração de 9,8 m / s². Portanto, 1 kg_f é igual a 9,8 N.
O peso P do menino é, então, 50 kg * 9,8 m / s² = 490 N
Durante a aceleração, a escala exerce uma força N no menino de 58 kg_f equivalente a 58 kg * 9,8 m / s² = 568,4 N.
A aceleração do elevador será dada por:
a = N / M - g = 568,4 N / 50 kg - 9,8 m / s² = 1,57 m / s²
A velocidade adquirida pelo elevador após 1,5 s com aceleração de 1,57 m / s² é:
v = a * t = 1,57 m / s² * 1,5 s = 2,36 m / s = 8,5 Km / h
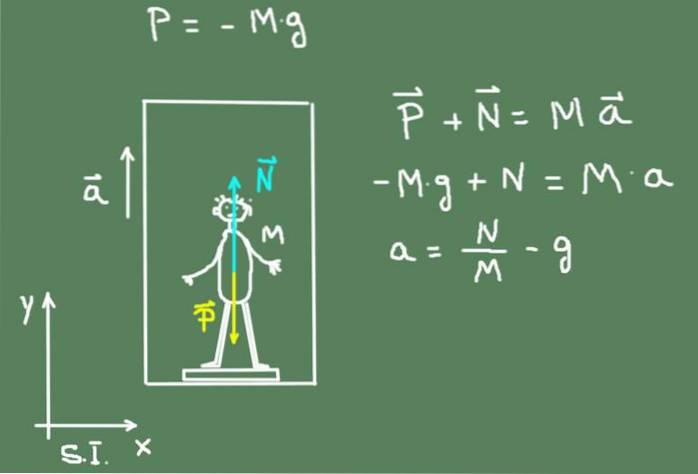
A figura a seguir mostra um diagrama das forças agindo sobre o menino:
O pote de maionese
Um menino entrega ao irmão o pote de maionese para o irmão, que está do outro lado da mesa. Para isso, conduz de forma que adquira uma velocidade de 3 m / s. A partir do momento em que a garrafa foi liberada até parar na extremidade oposta da mesa, o percurso foi de 1,5 m.
Determine o valor da força de atrito que a mesa exerce sobre a garrafa, sabendo que ela tem massa de 0,45 kg.
Solução
Primeiro determinaremos a aceleração de frenagem. Para isso, usaremos a seguinte relação, já conhecida a partir do movimento retilíneo uniformemente acelerado:
Vf² = Vi² + 2 * a * d
Onde Vf é a velocidade final, Serrar velocidade inicial, para aceleração e d o deslocamento.
A aceleração obtida na relação anterior é, onde o deslocamento da garrafa foi tomado como positivo.
a = (0 - 9 (m / s) ²) / (2 * 1,5 m) = -3 m / s²
A força resultante no pote de maionese é a força de atrito, já que o normal e o peso do pote se equilibram: Fnet = Fr.
Fr = m * a = 0,45 kg * (-3 m / s²) = -1,35 N = -0,14 kg-f
Experiências para crianças
Crianças e adultos podem realizar experiências simples que lhes permitem verificar se a segunda lei de Newton realmente funciona na vida real. Aqui estão dois muito interessantes:
Experimento 1
Um experimento simples requer uma balança de banheiro e um elevador. Pegue um peso de banheiro em um elevador e registre os valores marcados durante o início de subida, de descida e durante o tempo em que você está se movendo em velocidade constante. Calcule as acelerações do elevador para cada caso.
Experimento 2
- Pegue um carrinho de brinquedo que tenha as rodas bem lubrificadas
- Prenda uma corda até o final.
- Na borda da mesa, cole um lápis ou outro objeto cilíndrico liso sobre o qual o barbante passará..
- Na outra ponta da corda, pendure uma pequena cesta, na qual você colocará algumas moedas ou algo que sirva de peso..
O esquema do experimento é mostrado abaixo:
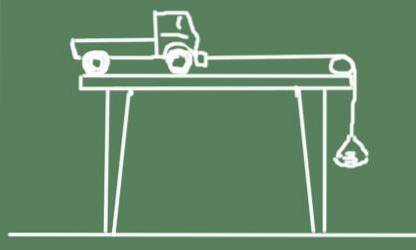
- Largue o carrinho e observe-o acelerar.
- Em seguida, aumente a massa do carrinho colocando moedas sobre ele, ou algo que aumente sua massa..
- Diga se a aceleração aumenta ou diminui. Coloque mais massa no carrinho, observe a aceleração e finalize.
O carrinho é então deixado sem peso extra e pode acelerar. Mais peso é então colocado na cesta para aumentar a força aplicada ao carrinho..
- Compare a aceleração com o caso anterior, indique se aumenta ou diminui. Você pode repetir adicionando mais peso à cesta e observar a aceleração do carrinho.
- Indique se aumenta ou diminui.
- Analise seus resultados e diga se eles concordam ou não com a segunda lei de Newton.
Artigos de interesse
Exemplos da Segunda Lei de Newton.
Primeira lei de newton.
Exemplos da Segunda Lei de Newton.
Referências
- Alonso M., Finn E. 1970. Física, volume I: Mecânica. Fundo Interamericano de Educação S.A. 156-163.
- Hewitt, P. 2012. Conceptual Physical Science. Quinta edição. 41-46.
- Jovem, Hugh. 2015. University Physics with Modern Physics. 14º Ed. Pearson. 108-115.


Ainda sem comentários