
Semicírculo como calcular o perímetro, área, centróide, exercícios
O semicírculo é uma figura plana delimitada por um diâmetro da circunferência e um dos dois arcos circulares planos determinados pelo referido diâmetro.
Desta forma, um semicírculo é delimitado por um semicircunferência, que consiste em um arco circular plano e um segmento reto que une as extremidades do arco circular plano. O semicírculo abrange o semicírculo e todos os pontos dentro dele..
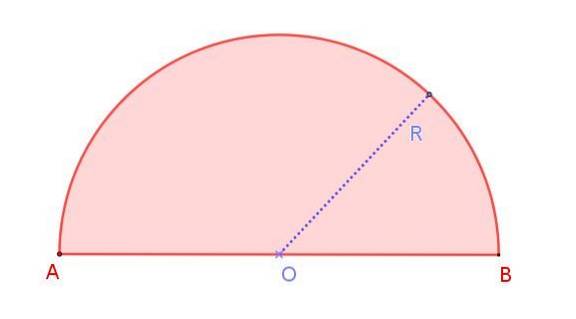
Podemos ver isso na figura 1, que mostra um semicírculo de raio R, cuja medida é a metade do diâmetro AB. Note que ao contrário de um círculo, no qual existem diâmetros infinitos, na semicircunferência existe apenas um diâmetro.
O semicírculo é uma figura geométrica com diversos usos na arquitetura e no design, como podemos ver na imagem a seguir:

Índice do artigo
- 1 Elementos e medidas de um semicírculo
- 1.1 Perímetro de um semicírculo
- 1.2 Área de um semicírculo
- 1.3 Centróide de um semicírculo
- 1.4 Momento de inércia de um semicírculo
- 1.5 Ângulo inscrito
- 2 exercícios resolvidos
- 2.1 Exercício 1
- 2.2 Exercício 2
- 2.3 Exercício 3
- 2.4 Exercício 4
- 2.5 Exercício 5
- 3 referências
Elementos e medidas de um semicírculo
Os elementos de um semicírculo são:
1.- O arco circular plano A⌒B
2.- O segmento [AB]
3.- Os pontos dentro do semicírculo composto pelo arco A⌒B e o segmento [AB].
Perímetro de um semicírculo
O perímetro é a soma do contorno do arco mais aquele do segmento reto, portanto:
Perímetro = comprimento do arco A⌒B + comprimento do segmento [AB]
No caso de um semicírculo de raio R, seu perímetro P será dado pela fórmula:
P = π⋅R + 2⋅R = (π + 2) ⋅R
O primeiro termo é a metade do perímetro de um círculo de raio R, enquanto o segundo é o comprimento do diâmetro, que é o dobro do raio..
Área de um semicírculo
Como um semicírculo é um dos setores angulares planos que permanecem ao desenhar um diâmetro através da circunferência, sua área A será a metade da área do círculo que contém o semicírculo de raio R:
A = (π⋅Rdois) / 2 = ½ π⋅Rdois
Centróide de um semicírculo
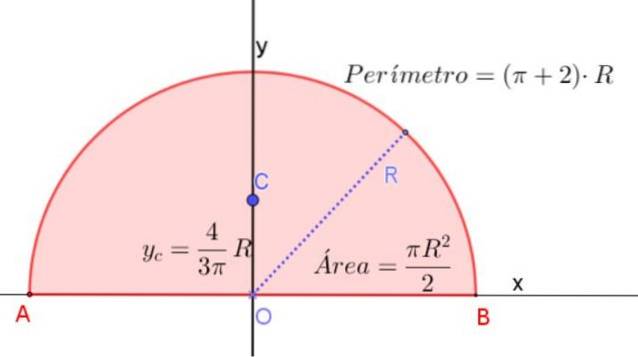
O centróide de um semicírculo está em seu eixo de simetria a uma altura medida a partir de seu diâmetro de 4 / (3π) vezes o raio R.
Isso corresponde a aproximadamente 0,424⋅R, medido a partir do centro do semicírculo e em seu eixo de simetria, conforme mostrado na figura 3.
Momento de inércia de um semicírculo
O momento de inércia de uma figura plana em relação a um eixo, por exemplo, o eixo x, é definido como:
A integral do quadrado da distância dos pontos pertencentes à figura ao eixo, sendo o diferencial de integração um elemento infinitesimal de área, tomado na posição de cada ponto.
A Figura 4 mostra a definição do momento de inércia Ix do semicírculo de raio R, em relação ao eixo X que passa por sua diagonal:
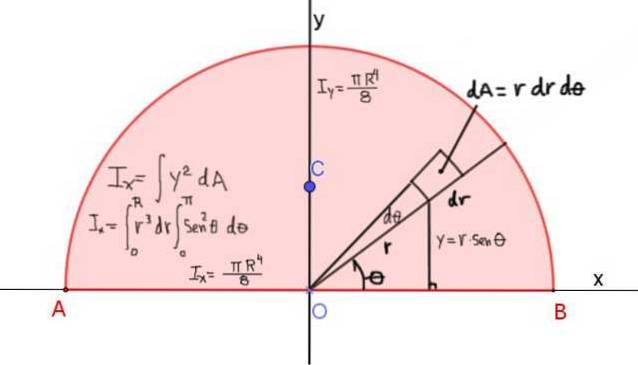
O momento de inércia em torno do eixo x é dado por:
eux = (π⋅R4) / 8
E o momento de inércia em relação ao eixo de simetria y é:
Iy = (π⋅R4) / 8
Nota-se que ambos os momentos de inércia coincidem em suas fórmulas, mas é importante destacar que se referem a eixos distintos..
Ângulo inscrito
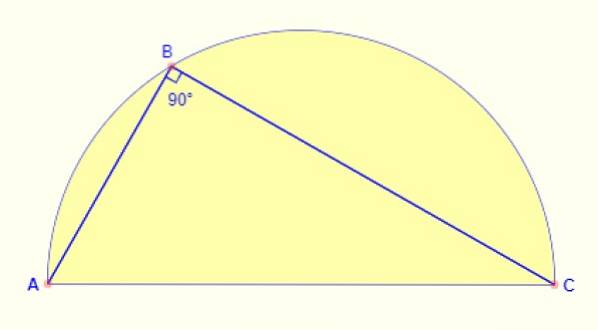
O ângulo inscrito no semicírculo é sempre 90º. Independentemente de onde o ponto é tirado no arco, o ângulo formado entre os lados AB e BC da figura está sempre correto..
Exercícios resolvidos
Exercício 1
Determine o perímetro de um semicírculo de raio de 10 cm.
Solução
Lembre-se de que o perímetro em função do raio é dado pela fórmula que vimos anteriormente:
P = (2 + π) ⋅R
P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.
Exercício 2
Encontre a área de um semicírculo com raio de 10 cm.
Solução
A fórmula para a área de um semicírculo é:
A = ½ π⋅Rdois = ½ π⋅ (10cm)dois = 50π cmdois = 50 x 3,14 cmdois = 157 cmdois.
Exercício 3
Determine a altura h do centróide de um semicírculo de raio R = 10 cm medido a partir de sua base, sendo o diâmetro do semicírculo o mesmo.
Solução
O centróide é o ponto de equilíbrio do semicírculo e sua posição está no eixo de simetria a uma altura h da base (diâmetro do semicírculo):
h = (4⋅R) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4,246 cm
Exercício 4
Encontre o momento de inércia de um semicírculo em relação ao eixo que coincide com seu diâmetro, sabendo que o semicírculo é feito de uma folha fina. Seu raio é de 10 cm e sua massa é de 100 gramas.
Solução
A fórmula que dá o momento de inércia do semicírculo é:
eux = (π⋅R4) / 8
Mas, uma vez que o problema nos diz que é um semicírculo material, a relação anterior deve ser multiplicada pela densidade superficial da massa do semicírculo, que será denotada por σ.
eux = σ (π⋅R4) / 8
Em seguida, passamos a determinar σ, que nada mais é do que a massa do semicírculo dividido por sua área.
A área foi determinada no exercício 2 e o resultado foi de 157 cmdois. Então, a densidade da superfície deste semicírculo será:
σ = 100 gramas / 157 cmdois = 0,637 g / cmdois
Então, o momento de inércia em relação ao diâmetro será calculado assim:
eux = (0,637 g / cmdois) [3,1416 ⋅ (10cm)4] / 8
Resultando:
eux = 2502 g⋅cmdois
Exercício 5
Determine o momento de inércia de um semicírculo de raio de 10 cm feito de uma folha de material com densidade superficial de 0,637 g / cmdois ao longo de um eixo que passa pelo seu centróide e é paralelo ao seu diâmetro.
Solução
Para resolver este exercício, é necessário lembrar o teorema de Steiner sobre os momentos de inércia de eixos paralelos, que diz:
O momento de inércia I em relação a um eixo que está a uma distância h do centróide é igual à soma do momento de inércia Ic em relação a um eixo que passa pelo centróide e é paralelo ao primeiro mais o produto da massa pelo quadrado da separação dos dois eixos.
Eu = euc + M hdois
No nosso caso, sabe-se I qual é o momento de inércia em relação ao diâmetro, que já foi calculado no exercício 4. Também é conhecida a separação h entre o diâmetro e o centróide, que foi calculada no exercício 3.
Só temos que limpar Ic:
euc = I - M hdois
euc = 2502 g⋅cmdois - 100g ⋅ (4,246 cm)dois dando como resultado que o momento de inércia através de um eixo paralelo ao diâmetro e passando pelo centróide é:
euc = 699,15 g⋅cmdois
Referências
- Alexander, D. 2013. Geometria. 5 ª. Edição. Cengage Learning.
- Referência de matemática aberta. Semicírculo. Recuperado de: mathopenref.com.
- Universe Formulas Semicircle. Recuperado de: universoformulas.com.
- Fórmulas do universo. Área de um semicírculo. Recuperado de: universoformulas.com.
- Wikipedia. Semicírculo. Recuperado de: en.wikipedia.com.



Ainda sem comentários