Exemplos e exercícios de séries de poder

UMA série de poder consiste em um somatório de termos na forma de poderes da variável x, ou mais geralmente, de x-c, Onde c é um número real constante. Em notação de soma, uma série de poderes é expressa da seguinte forma:

∑a_n (x -c)ⁿ = a_ou + para₁ (x - c) + a_dois (x - c)^dois + para₃ (x - c)³ +… + A_n (x - c)ⁿ

Onde os coeficientes a_ou, para₁, para_dois… São números reais e a série começa em n = 0.

Esta série é focada em valor c que é constante, mas você pode escolher qual c é igual a 0, caso em que a série de potências simplifica para:

∑a_n xⁿ = a_ou + para₁ x + a_dois x^dois + para₃ x³ +… + A_n xⁿ

A série começa com para_ou(x-c)⁰ Y para_oux⁰ respectivamente. Mas sabemos que:

(x-c)⁰= x⁰ = 1

Portanto para_ou(x-c)⁰ = para_oux⁰ = para_ou (termo independente)

A coisa boa sobre as séries de potência é que você pode expressar funções com elas e isso tem muitas vantagens, especialmente se você quiser trabalhar com uma função complicada.

Quando for o caso, em vez de usar a função diretamente, usa-se sua expansão em série de potências, que pode ser mais fácil de derivar, integrar ou trabalhar numericamente..

Claro, tudo está condicionado à convergência das séries. Uma série converge quando a adição de um certo grande número de termos dá um valor fixo. E se adicionarmos mais termos ainda, continuamos a obter esse valor.

Índice do artigo

• 1 Funciona como Power Series
  • 1.1 Série geométrica de potência
• 2 Como encontrar a expansão em série de poderes de uma função
• 3 exercício
  • 3.1 - Exercício resolvido 1
  • 3.2 - Exercício resolvido 2
• 4 referências

Funções como Power Series

Como exemplo de uma função expressa como uma série de potências, vamos tomar f (x) = e^x.

Esta função pode ser expressa em termos de uma série de poderes da seguinte forma:

e^x  ≈ 1 + x + (x^dois / 2!) + (X³ / 3!) + (X⁴ / 4!) + (X⁵ / 5!) + ...

Onde! = n. (n-1). (n-2). (n-3) ... e leva 0! = 1.

Vamos verificar com a ajuda de uma calculadora, se de fato a série coincide com a função dada explicitamente. Por exemplo, vamos começar fazendo x = 0.

Nós sabemos que e⁰ = 1. Vamos ver o que a série faz:

e⁰ ≈ 1 + 0 + (0^dois / 2!) + (0³ / 3!) + (0⁴ / 4!) + (0⁵ / 5!) +… = 1

E agora vamos tentar com x = 1. Uma calculadora mostra que e¹ = 2.71828, e então vamos comparar com a série:

e¹ ≈ 1 + 1 + (1^dois / 2!) + (1³ / 3!) + (1⁴ / 4!) + (1⁵ / 5!) + ... = 2 + 0,5000 + 0,1667 + 0,0417 + 0,0083 + ... ≈ 2,7167

Com apenas 5 termos, já temos uma correspondência exata em e ≈ 2,71. Nossa série ainda tem um pouco mais, mas à medida que mais termos são adicionados, a série certamente converge para o valor exato de e. A representação é exata quando n → ∞.

Se a análise acima for repetida para n = 2 resultados muito semelhantes são obtidos.

Desta forma, temos certeza de que a função exponencial f (x) = e^x pode ser representado por esta série de poderes:

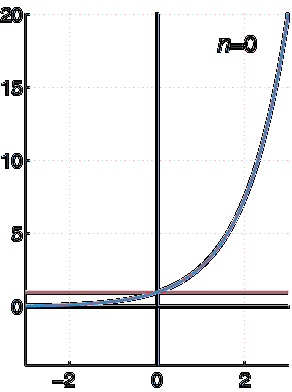
Série geométrica de poderes

A função f (x) = e^x não é a única função que suporta uma representação de série de potências. Por exemplo, a função  F(x) = 1/1 - x  se parece muito com o conhecido série geométrica convergente:

∑a.rⁿ = a / 1 - r

Basta fazer a = 1 e r = x para obter uma série adequada a esta função, que está centrada em c = 0:

Porém, sabe-se que esta série é convergente para │r│<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.

Quando você quiser definir essa função em outro intervalo, basta focar em um valor adequado e pronto..

Como encontrar a expansão em série de poderes de uma função

Qualquer função pode ser desenvolvida em uma série de potências centrada em c, desde que tenha derivadas de todas as ordens em x = c. O procedimento faz uso do seguinte teorema, chamado Teorema de Taylor:

Seja f (x) uma função com derivadas de ordem n, denotado como F⁽ⁿ⁾, que admite uma expansão em série de poderes no intervalo eu. Seu desenvolvimento em Taylor Series isso é:

De maneira que:

f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)^dois / 2 + f "(c) (x-c)³ / 6 +… R_n

Onde R_n, que é o enésimo termo da série, é chamado resíduo:

Quando c = 0 a série é chamada Maclaurin series.

Esta série dada aqui é idêntica à série dada no início, só que agora temos uma maneira de encontrar explicitamente os coeficientes de cada termo, dados por:

No entanto, deve-se garantir que a série converge para a função a ser representada. Acontece que nem toda série de Taylor converge necessariamente para o f (x) que se tinha em mente no cálculo dos coeficientes. para_n.

Isso acontece porque talvez as derivadas da função, avaliadas em x = c coincidir com o mesmo valor das derivadas de outra, também em x = c. Nesse caso, os coeficientes seriam os mesmos, mas o desenvolvimento seria ambíguo, pois não se sabe ao certo a qual função ele corresponde..

Felizmente, existe uma maneira de saber:

Critério de convergência

Para evitar ambigüidade, se R_n → 0 quando n → ∞ para todo x no intervalo I, a série converge para f (x).

Exercício

- Exercício 1 resolvido

Encontre a série geométrica de potência para a função f (x) = 1/2 - x centrado em c = 0.

Solução

A função dada deve ser expressa de tal forma que coincida o mais possível com 1 / 1- x, cuja série é conhecida. Portanto, vamos reescrever o numerador e o denominador, sem alterar a expressão original:

1/2 - x = (1/2) / [1 - (x / 2)]

Como ½ é constante, ele sai da soma e é escrito em termos da nova variável x / 2:

Observe que x = 2 não pertence ao domínio da função, e de acordo com o critério de convergência dado na seção Série de potência geométrica, a expansão é válida para │x / 2│< 1 o equivalentemente -2 < x < 2.

- Exercício resolvido 2

Encontre os 5 primeiros termos da expansão da série Maclaurin da função f (x) = sin x.

Solução

Passo 1

Os derivados são encontrados pela primeira vez:

-Derivada de ordem 0: é a mesma função f (x) = sin x

-Primeira derivada: (sin x) '= cos x

-Segunda derivada: (sin x) "= (cos x) '= - sin x

-Terceira derivada: (sin x) "= (-sen x) '= - cos x

-Quarta derivada: (sin x) "= (- cos x) '= sin x

Passo 2

Então, cada derivada é avaliada em x = c, como é uma expansão de Maclaurin, c = 0:

sen 0 = 0; cos 0 = 1; - sen 0 = 0; -cos 0 = -1; sin 0 = 0

etapa 3

Os coeficientes a são construídos_n;

para_ou = 0/0! = 0; para₁ = 1/1! = 1; para_dois = 0/2! = 0; para₃ = -1 / 3!; para₄ = 0/4! = 0

Passo 4

Finalmente, a série é montada de acordo com:

sen x ≈ 0.x⁰ + 1. x¹ + 0 .x^dois - (1/3!) X³ + 0.x⁴… = X - (1/3!)) X³  +...

O leitor precisa de mais termos? Quanto mais, a série se aproxima da função.

Observe que há um padrão nos coeficientes, o próximo termo diferente de zero é um₅ e todos aqueles com índice ímpar também são diferentes de 0, alternando os sinais, de modo que:

sin x ≈ x - (1/3!)) x³  + (1/5!)) X⁵ - (1/7!)) X⁷  +... .

É deixado como um exercício para verificar se ele converge, você pode usar o critério de quociente para convergência de série.

Referências

1. Fundação CK-12. Power Series: representação de funções e operações. Recuperado de: ck12.org.
2. Engler, A. 2019. Integral Calculus. Universidade Nacional do Litoral.
3. Larson, R. 2010. Cálculo de uma variável. 9º. Edição. Colina Mcgraw.
4. Textos Livres de Matemática. Série de potências. Recuperado de: math.liibretexts.org.
5. Wikipedia. Série de potências. Recuperado de: es.wikipedia.org.