
Sólidos de volume de revolução, tipos, exercícios resolvidos
O sólido de revolução É a figura tridimensional gerada pela rotação de uma superfície plana em torno do eixo axial ou eixo de revolução. A Figura 1 mostra a animação de um sólido de revolução gerado desta forma.
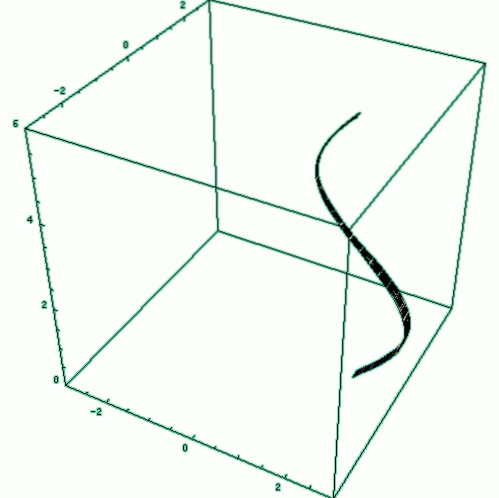
Outro exemplo muito fácil de visualizar consiste em gerar um cilindro circular reto, girando um retângulo de altura ou comprimento he raio r, em torno do eixo x positivo (figura 2). Para encontrar seu volume, existe uma fórmula bem conhecida:
V = área da base x altura
Outros sólidos de revolução são a esfera, o cone circular direito e várias figuras, dependendo da superfície colocada em rotação e, claro, o eixo selecionado..
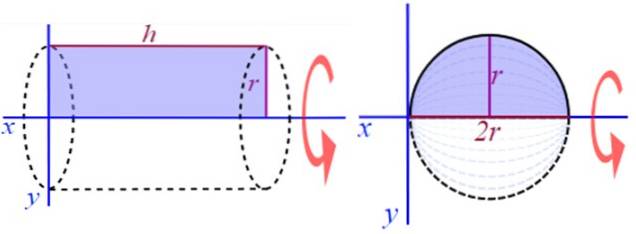
Por exemplo, girar o semicírculo em torno de uma linha paralela ao diâmetro dá um sólido de revolução oca.
Para o cilindro, o cone, a esfera, tanto sólida como oca, existem fórmulas para encontrar o volume, que depende do raio e da altura. Mas quando eles são gerados por outras superfícies, o volume é calculado por integrais definidas.
Índice do artigo
- 1 Tipos de sólidos de revolução
- 1.1 Esfera
- 1,2 cone
- 1.3 Cilindro
- 1.4 Toróide
- 2 Métodos para calcular o volume de um sólido de revolução
- 2.1 Método de disco ou lavadora
- 2.2 Método de camada
- 3 Exercício resolvido
- 4 referências
Tipos de sólidos de revolução
Os sólidos de revolução podem ser classificados de acordo com a curva que os gera:
Esfera
Basta girar um semicírculo em torno de um eixo que será o diâmetro da esfera do raio R. Seu volume é:
Vesfera = (4/3) πR3
Cone
Para obter um cone de altura H e raio R, a superfície a ser girada é um triângulo retângulo, em torno do eixo axial que passa por uma das pernas. Seu volume é:
Vcone = (1/3) πHRdois
Cilindro
Girando um retângulo em torno de um eixo axial que passa por um dos lados, que pode ser o lado curto ou o lado longo, obtemos um cilindro circular reto de raio R e altura H, cujo volume é:
Vcilindro = πRdoisH
Toróide
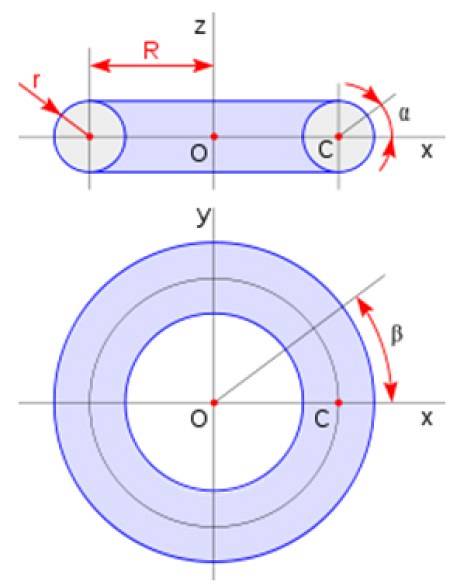
O toro tem a forma de um donut. É obtido girando uma região circular em torno de uma linha no plano que não intercepta o círculo. Seu volume é dado por:
Vtoro = 2πadoisR
Onde a é o raio da seção transversal e R é o raio do toro de acordo com o esquema apresentado na figura:
Métodos para calcular o volume de um sólido de revolução
No cálculo integral, esses dois métodos são frequentes:
-Discos e arruelas
-Cartuchos
Método de disco ou lavadora
Ao fatiar um sólido de revolução, a seção transversal pode ser um disco, se o sólido for sólido, ou pode ser uma espécie de arruela (um disco com um furo no meio), se for um sólido oco..
Suponha que uma região plana seja girada em torno do eixo horizontal. Desta região plana, pegamos um pequeno retângulo de largura Δx, que é girado perpendicularmente ao redor do eixo axial.
A altura do retângulo está entre a curva mais externa R (x) e a curva mais interna r (x). Eles correspondem ao raio externo e ao raio interno, respectivamente..
Ao fazer essa rotação, uma arruela de volume ΔV é gerada, dada por:
ΔV = volume total - volume do orifício (se houver)
Lembrando que o volume de um cilindro circular reto é π. rádiodois x altura, temos:
ΔV = π [Rdois(x) - rdois(x)] Δx
O sólido pode ser dividido em uma infinidade de pequenas porções de volume ΔV. Se adicionarmos todos eles, teremos o volume total.
Para isso, fazemos com que o volume ΔV tenda a 0, com o qual Δx também se torna muito pequeno, tornando-se um dx diferencial.
Portanto, temos uma integral:
V = ∫parab π [Rdois(x) - rdois(x)] dx
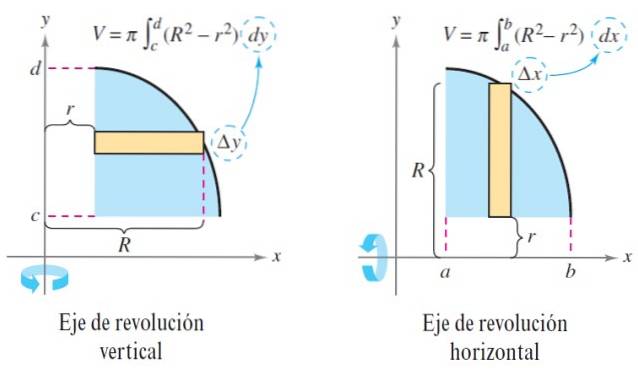
Caso o sólido seja sólido, então a função r (x) = 0, a fatia do sólido que é gerada é um disco e o volume permanece:
V = ∫parab πRdois(x) dx
Quando o eixo de revolução é vertical, as equações acima assumem a forma:
V = ∫parab π [Rdois (y) - rdois (y)] dy y V = ∫parab πRdois(y) dy
Método de camada
Como o próprio nome indica, este método consiste em assumir que o sólido é composto por camadas de espessura diferencial. A camada é um tubo fino que se origina da rotação de um retângulo paralelo ao eixo de rotação.
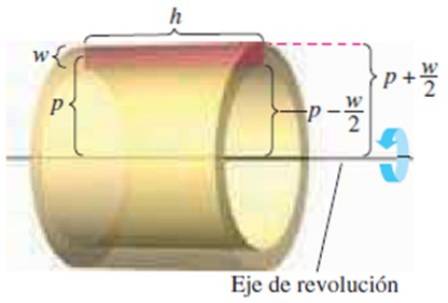
Temos as seguintes dimensões:
-A altura do retângulo C
-Sua longitude h
-A distância do centro do retângulo ao eixo de rotação p
Saber que o volume da camada é volume exterior - volume interior:
π (p + w / 2)doish - π (p - w / 2)doish
Ao desenvolver e simplificar produtos notáveis, você obtém:
Volume da camada = 2π⋅p⋅w⋅h
Agora vamos fazer a altura w do retângulo Δy, como pode ser visto na figura a seguir:
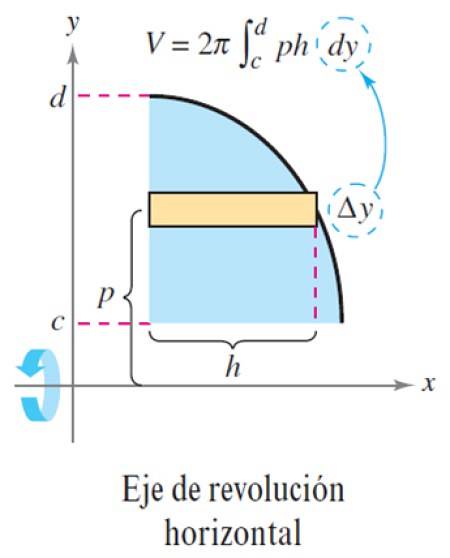
Com isso, o volume ΔV é:
ΔV = 2π p x h x Δy
E fazendo o número de camadas n é muito grande, Δy torna-se um dy diferencial, com o qual o volume total é o integral:
V = ∫cd 2π p (y) h (y) dy
O procedimento descrito se aplica de forma semelhante quando o eixo de revolução é vertical:
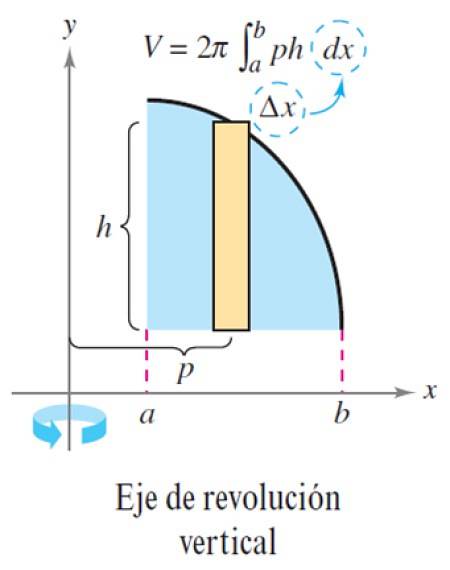
Exercício resolvido
Encontre o volume gerado pela rotação da região do plano entre as curvas:
y = xdois; y = 0; x = 2
Em torno do eixo y.
Solução
-A primeira coisa que devemos fazer é representar graficamente a região que irá gerar o sólido de revolução e indicar o eixo de rotação. Temos isso no gráfico a seguir:
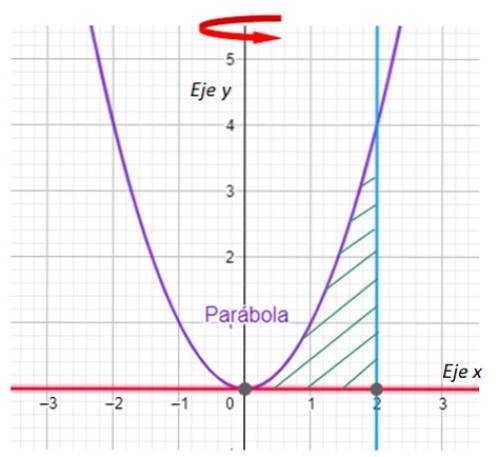
-Agora estamos procurando as interseções entre a curva y = xdois e a linha x = 2. Por sua vez, a linha y = 0 nada mais é do que o eixo x.
No gráfico é fácil ver que a parábola e a reta se cruzam no ponto (2,4), o que é corroborado pela substituição de x = 2 em y = xdois.
-Em seguida, um dos métodos para calcular o volume é escolhido, por exemplo, o método de camada com eixo vertical de revolução:
V = ∫parab 2π p (x) h (x) dx
Etapa 1: desenhe o retângulo
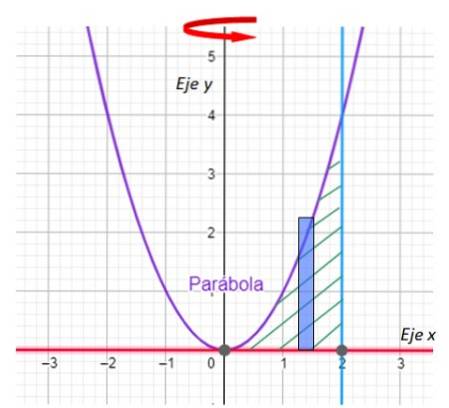
Importante: No método de estratificação, o lado longo do retângulo é paralelo ao eixo de rotação.
Etapa 2: determinar p (x)
O raio da camada é x
Etapa 3: determinar h (x)
A altura do retângulo é determinada pela parábola xdois.
Etapa 4: estabelecer e resolver o volume integral
A variável de integração é x, que varia entre 0 e 2, com isso temos os limites da integração. Substituindo as expressões por p (x) e h (x)

Referências
- Larson, R. 2010. Cálculo de uma variável. 9º. Edição. Colina Mcgraw.
- Purcell, E. 2007. Calculus with Analytical Geometry. 9º. Edição. Pearson Education.
- Wikipedia. Sólido de revolução. Recuperado de: en.wikipedia.org.
- Wikipedia. Toróide Recuperado de: es.wikipedia.org.
- Wolfram MathWorld. Sólido de revolução. Recuperado de: mathworld.wolfram.com.



Ainda sem comentários