
Método de suavização exponencial e exemplo
O suavização exponencial é uma forma de prever a demanda de um item para um determinado período. Este método estima que a demanda será igual à média do consumo histórico em um determinado período, dando um peso ou peso maior aos valores que estão mais próximos no tempo. Além disso, para as seguintes previsões, leve em consideração o erro existente da previsão atual.
A previsão de demanda é o método de projetar a demanda do cliente por um produto ou serviço. Esse processo é contínuo, em que os gerentes usam dados históricos para calcular o que esperam ser a demanda de vendas de um bem ou serviço..
As informações do passado da empresa são usadas adicionando-as aos dados econômicos do mercado para ver se as vendas vão aumentar ou diminuir.
Os resultados da previsão de demanda são utilizados para traçar metas para o departamento de vendas, buscando ficar em linha com os objetivos da empresa.
Índice do artigo
- 1 Método de suavização exponencial
- 1.1 Suavização na previsão
- 1.2 Média móvel ponderada
- 1.3 Suavização exponencial
- 2 exemplo
- 3 referências
Método de suavização exponencial
A suavização é um processo estatístico muito comum. Os dados suavizados são freqüentemente encontrados em várias formas da vida cotidiana. Cada vez que uma média é usada para descrever algo, um número suavizado está sendo usado.
Suponha que o inverno mais quente já registrado tenha ocorrido este ano. Para quantificá-lo, começamos com o conjunto de dados diários de temperatura para o período de inverno de cada ano histórico registrado..
Isso gera uma série de números com grandes “saltos”. Você precisa de um número que elimine todos esses saltos dos dados para poder comparar mais facilmente um inverno com outro.
A eliminação do salto nos dados é chamada de suavização. Neste caso, uma média simples pode ser usada para alcançar a suavização.
Suavização na previsão
Para previsão de demanda, a suavização também é usada para eliminar variações na demanda histórica. Isso permite uma melhor identificação dos padrões de demanda, que podem ser usados para estimar a demanda futura..
Variações na demanda são o mesmo conceito que o "salto" dos dados de temperatura. A maneira mais comum de remover variações no histórico de demanda é usando uma média ou, especificamente, uma média móvel..
A média móvel usa um número predefinido de períodos para calcular a média, e esses períodos mudam com o passar do tempo..
Por exemplo, se uma média móvel de quatro meses for usada e hoje for 1º de maio, será usada a demanda média de janeiro, fevereiro, março e abril. No dia 1º de junho, será utilizada a demanda de fevereiro, março, abril e maio.
Média móvel ponderada
Ao usar uma média simples, a mesma importância é aplicada a cada valor no conjunto de dados. Portanto, em uma média móvel de quatro meses, cada mês representa 25% da média móvel..
Ao usar o histórico de demanda para projetar a demanda futura, é lógico que o período mais recente tem um impacto maior na previsão..
Você pode adaptar o cálculo da média móvel para aplicar diferentes "pesos" a cada período, a fim de obter os resultados desejados..
Esses pesos são expressos como porcentagens. O total de todos os pesos para todos os períodos deve somar 100%.
Portanto, se você deseja aplicar 35% como o peso para o período mais próximo na média ponderada de quatro meses, você pode subtrair 35% de 100%, deixando 65% para dividir entre os três períodos restantes.
Por exemplo, você pode acabar com uma ponderação de 15%, 20%, 30% e 35%, respectivamente, para os quatro meses (15 + 20 + 30 + 35 = 100).
Suavização exponencial
A entrada de controle para o cálculo de suavização exponencial é conhecida como fator de suavização. Representa o peso aplicado à demanda para o período mais recente.
Se 35% for usado como o peso do período mais recente no cálculo da média móvel ponderada, você também pode escolher usar 35% como o fator de suavização no cálculo de suavização exponencial..
Parte exponencial
A diferença no cálculo de suavização exponencial é que em vez de ter que descobrir quanto peso aplicar a cada período anterior, o fator de suavização é usado para fazer isso automaticamente..
Esta é a parte "exponencial". Se 35% for usado como o fator de suavização, o peso da demanda para o período mais recente será de 35%. A ponderação da demanda do período anterior para o mais recente será de 65% a 35%.
65% vem subtraindo 35% de 100%. Isso equivale a 22,75% de ponderação para esse período. A demanda do próximo período mais recente será de 65% de 65% de 35%, o que equivale a 14,79%.
O período anterior será ponderado como 65% de 65% de 65% de 35%, equivalente a 9,61%. Isso será feito para todos os períodos anteriores, até o primeiro período.
Fórmula
A fórmula para calcular a suavização exponencial é a seguinte: (D * S) + (P * (1-S)), onde,
D = demanda mais recente do período.
S = fator de suavização, representado na forma decimal (35% seria 0,35).
P = previsão do período mais recente, resultado do cálculo de suavização do período anterior.
Supondo que temos um fator de suavização de 0,35, teríamos: (D * 0,35) + (P * 0,65).
Como você pode ver, as únicas entradas de dados necessárias são a demanda e a previsão do período mais recente..
Exemplo
Uma seguradora decidiu expandir seu mercado para a maior cidade do país, oferecendo seguros para veículos.
Como ação inicial, a empresa quer prever quanto seguro de veículos será adquirido pelos moradores desta cidade.
Para fazer isso, eles usarão como dados iniciais o valor do seguro automóvel adquirido em outra cidade menor.
A previsão de demanda para o período 1 é de 2.869 seguros de veículos contratados, mas a demanda real nesse período foi de 3.200.
A critério da empresa, ele atribui um fator de suavização de 0,35. A demanda prevista para o seguinte período é: P2 = (3200 * 0,35) + 2869 * (1-0,35) = 2984,85.
Esse mesmo cálculo foi feito para todo o ano, obtendo-se a seguinte tabela comparativa entre o que foi efetivamente obtido e o que foi previsto para aquele mês.
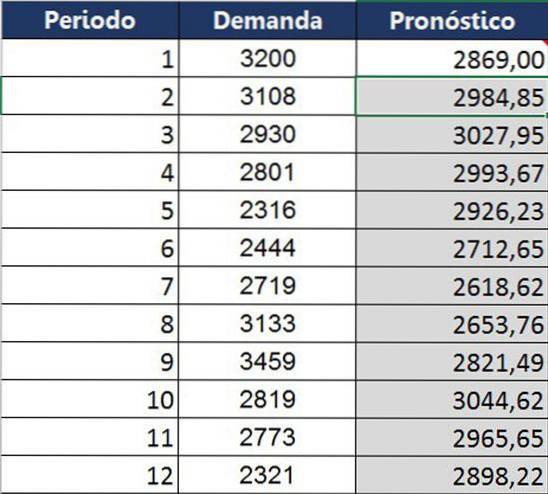
Em comparação com as técnicas de média, a suavização exponencial pode prever melhor a tendência. No entanto, ainda é insuficiente, conforme mostrado no gráfico:
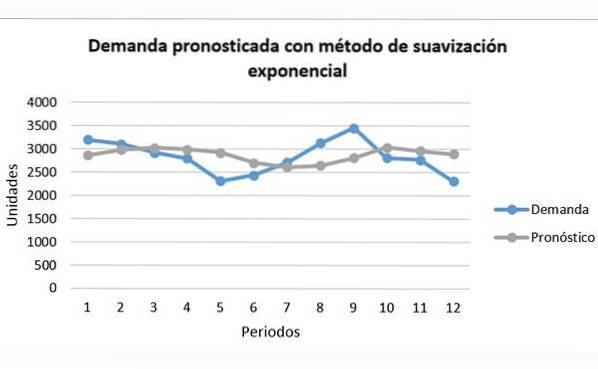
Pode-se ver como a linha cinza da previsão pode estar bem abaixo ou acima da linha azul da demanda, sem ser capaz de segui-la totalmente.
Referências
- Wikipedia (2019). Suavização exponencial. Retirado de: es.wikipedia.org.
- Ingenio Empresa (2016). Como usar a suavização exponencial simples para prever a demanda. Retirado de: ingenioempresa.com.
- Dave Piasecki (2019). Suavização exponencial explicada. Retirado de: inventoryops.com.
- Study (2019). Técnicas de previsão de demanda: Média móvel e suavização exponencial. Retirado de: study.com.
- Cityu (2019). Métodos de suavização exponencial. Retirado de: personal.cb.cityu.edu.hk.


Ainda sem comentários