Exemplos de sequências quadráticas, regras e exercícios resolvidos

As sequências quadráticas, em termos matemáticos, eles consistem em sequências de números que seguem uma certa regra aritmética. É interessante conhecer esta regra para determinar qualquer um dos termos de uma sequência.

Uma forma de o conseguir é determinar a diferença entre dois termos sucessivos e verificar se o valor obtido se repete sempre. Quando este for o caso, é considerado um sucessão regular.

Mas se não for repetido, você pode tentar examinar o diferença entre diferenças e veja se esse valor é constante. Se sim, então é um seqüência quadrática. 

Índice do artigo

• 1 Exemplos de sequências regulares e sequências quadráticas
  • 1.1 Exemplo de sucessão regular
  • 1.2 Exemplo de sequência quadrática e não regular
• 2 Regra geral para a construção de uma sequência quadrática
  • 2.1 Diferença entre dois termos consecutivos de uma sequência quadrática
• 3 Problemas resolvidos de sequências quadráticas
  • 3.1 Exercício 1
  • 3.2 Exercício 2
  • 3.3 Exercício 3
• 4 referências

Exemplos de sequências regulares e sequências quadráticas

Os exemplos a seguir ajudam a esclarecer o que foi explicado até agora:

Exemplo de sucessão regular

Deixe a sequência S = 4, 7, 10, 13, 16, ...

Esta sequência, denotada por S, é um conjunto numérico infinito, neste caso de inteiros.

Percebe-se que se trata de uma sequência regular, pois cada termo é obtido adicionando 3 ao termo ou elemento anterior:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

Em outras palavras: esta sequência é regular porque a diferença entre o próximo termo e o anterior dá um valor fixo. No exemplo fornecido, este valor é 3.

As sequências regulares que são obtidas adicionando uma quantidade fixa ao termo anterior também são chamadas progressões aritméticas. E a diferença -constante- entre os termos sucessivos é chamada razão e é denotado como R.

Exemplo de sequência quadrática e não regular

Veja agora a seguinte sequência:

S = 2, 6, 12, 20, 30,….

Quando diferenças sucessivas são calculadas, os seguintes valores são obtidos:

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Suas diferenças não são constantes, então pode-se dizer que não é uma sequência regular.

No entanto, se considerarmos o conjunto de diferenças, temos outra sequência, que será denotada como S_diferença:

S_diferença = 4, 6, 8, 10,….

Esta nova sucessão é um sucessão regular, já que cada termo é obtido adicionando o valor fixo R = 2 ao anterior. Portanto, podemos afirmar que S é seqüência quadrática.

Regra geral para construir uma sequência quadrática

Existe uma fórmula geral para construir uma sequência quadrática:

T_n = A ∙ n^dois + B ∙ n + C

Nesta fórmula, T_n é o termo da posição n da sequência. A, B e C são valores fixos, enquanto n varia um a um, ou seja, 1, 2, 3, 4, ...

Na sequência S do exemplo anterior A = 1, B = 1 e C = 0. A partir daí, segue-se que a fórmula que gera todos os termos é: T_n = n^dois + n

Quer dizer:

T₁ = 1^dois + 1 = 2

T_dois = 2^dois + 2 = 6

T₃ = 3^dois + 3 = 12

T₅ = 5^dois + 5 = 30

T_n = n^dois + n

Diferença entre dois termos consecutivos de uma sequência quadrática

T_{n + 1} - T_n = [A ∙ (n + 1)^dois + B ∙ (n + 1) + C] - [A ∙ n^dois + B ∙ n + C]

O desenvolvimento da expressão por meio de produtos notáveis ​​permanece:

T_{n + 1} - T_n = A ∙ n^dois + A ∙ 2 ∙ n + A + B ∙ n + B + C - A ∙ n^dois - B ∙ n - C

Simplificando, você obtém:

T_{n + 1} - T_n = 2 ∙ A ∙ n + A + B

Esta é a fórmula que dá a sequência de diferenças S_Dif que pode ser escrito assim:

Dif_n = A ∙ (2n + 1) + B

Onde claramente o próximo termo é 2 ∙ Às vezes, o anterior. Ou seja, a razão da sequência de diferenças S_diferença é: R = 2 ∙ A.

Problemas resolvidos de sequências quadráticas

Exercício 1

Deixe a sequência S = 1, 3, 7, 13, 21,…. Determine se:

i) É regular ou não

ii) É quadrático ou não

iii) Foi quadrático, a sequência de diferenças e sua proporção

Respostas

i) Vamos calcular a diferença entre o seguinte e os termos anteriores:

3-1 = 2

7-3 = 4

13-7 = 6

21-13 = 8

Podemos afirmar que a sequência S não é regular, porque a diferença entre os termos sucessivos não é constante.

ii) A sequência de diferenças é regular, pois a diferença entre seus termos é o valor constante 2. Portanto a sequência original S é quadrática.

iii) Já determinamos que S é quadrático, a sequência de diferenças é:

S_diferença = 2, 4, 6, 8, ... e sua razão é R = 2.

Exercício 2

Seja a sequência S = 1, 3, 7, 13, 21,… do exemplo anterior, onde se verificou que é quadrática. Determinar:

i) A fórmula que determina o termo geral T_{n .}

ii) Verifique o terceiro e o quinto termos.

iii) O valor do décimo termo.

Respostas

i) A fórmula geral de T_n é A ∙ n^dois + B ∙ n + C. Então resta saber os valores de A, B e C.

A sequência de diferenças tem razão 2. Além disso, para qualquer sequência quadrática, a razão R é 2 ∙ A, conforme mostrado nas seções anteriores.

R = 2 ∙ A = 2 o que nos leva a concluir que A = 1.

O primeiro termo da sequência de diferenças S_Dif é 2 e deve satisfazer A ∙ (2n + 1) + B, com n = 1 e A = 1, ou seja:

2 = 1 ∙ (2 ∙ 1 + 1) + B

resolvendo para B, obtemos: B = -1

Então, o primeiro termo de S (n = 1) vale 1, ou seja: 1 = A ∙ 1^dois + B ∙ 1 + C. Como já sabemos que A = 1 e B = -1, substituindo temos:

1 = 1 ∙ 1^dois + (-1) ∙ 1 + C

Resolvendo para C, obtemos seu valor: C = 1.

Em resumo:

A = 1, B = -1 e C = 1

Então, o enésimo termo será T_n = n^dois - n + 1

ii) O terceiro termo T₃ = 3^dois - 3 + 1 = 7 e é verificado. O quinto T₅ = 5^dois - 5 + 1 = 21 que também é verificado.

iii) O décimo mandato será T₁₀ = 10^dois - 10 + 1 = 91.

Exercício 3

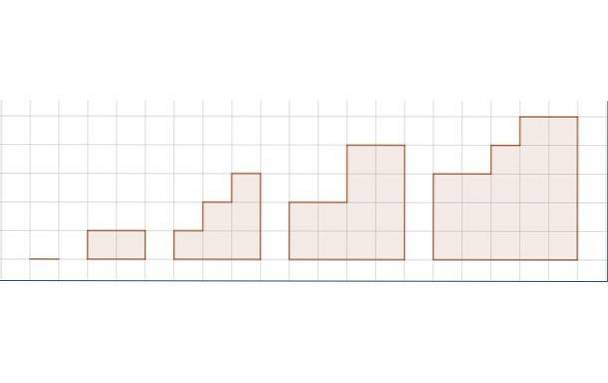
A figura mostra uma sequência de cinco figuras. A rede representa a unidade de comprimento.

i) Determine a sequência para a área das figuras.

ii) Mostre que é uma sequência quadrática.

iii) Encontre a área da figura # 10 (não mostrada).

Respostas

i) A sequência S correspondente à área da sequência de figuras é:

S = 0, 2, 6, 12, 20,…

ii) A sequência correspondente às diferenças consecutivas dos termos de S é:

S_diferença = 2, 4, 6, 8,…

Visto que a diferença entre os termos consecutivos não é constante, então S não é uma sequência regular. Resta saber se é quadrático, para o qual fazemos novamente a sequência das diferenças, obtendo:

2, 2, 2,….

Uma vez que todos os termos da sequência são repetidos, é confirmado que S é uma sequência quadrática.

iii) A sequência S_diferença é regular e sua razão R é 2. Usando a equação mostrada acima R = 2 ∙ A, permanece:

2 = 2 ∙ A, o que implica que A = 1.

O segundo termo da sequência de diferenças S_Dif é 4 e o enésimo termo de S_Dif isso é

A ∙ (2n + 1) + B.

O segundo termo possui n = 2. Além disso, já foi determinado que A = 1, então usando a equação anterior e substituindo, temos:

4 = 1 ∙ (2 ∙ 2 + 1) + B

Resolvendo para B, obtemos: B = -1.

Sabe-se que o segundo termo de S vale 2, e que deve cumprir a fórmula do termo geral com n = 2:

T_n = A ∙ n^dois + B * n + C; n = 2; A = 1; B = -1; T_dois = 2

Quer dizer

2 = 1 ∙ 2^dois - 1 ∙ 2 + C

Conclui-se que C = 0, ou seja, a fórmula que dá o termo geral da sequência S é:

T_n = 1 ∙ n^dois - 1 ∙ n +0 = n^dois - n

Agora o quinto termo é verificado:

T₅ = 5^dois - 5 = 20

iii) A Figura # 10, que não foi desenhada aqui, terá a área correspondente ao décimo termo da sequência S:

T₁₀ = 10^dois - 10 = 90

Referências

1. https://www.geogebra.org