
Soma de polinômios, como fazer, exemplos, exercícios
O soma de polinômios é a operação que consiste em adicionar dois ou mais polinômios, resultando em outro polinômio. Para realizá-lo é necessário somar os termos da mesma ordem de cada um dos polinômios e indicar a soma resultante.
Vamos primeiro revisar brevemente o significado de "termos da mesma ordem". Qualquer polinômio é feito de adições e / ou subtrações de termos.

Os termos podem ser produtos de números reais e uma ou mais variáveis, representadas por letras, por exemplo: 3xdois e -√5.adoisac3 são termos.
Bem, os termos da mesma ordem são aqueles que têm o mesmo expoente ou potência, embora possam ter um coeficiente diferente.
-Os termos de pedido iguais são: 5x3, √2 x3 e -1 / 2x3
-Termos de pedido diferentes: -2x-dois, 2xy-1 e √6xdoisY
É importante ter em mente que apenas termos da mesma ordem podem ser adicionados ou subtraídos, uma operação conhecida como redução. Caso contrário, a soma é simplesmente indicada à esquerda.
Uma vez que o conceito de termos da mesma ordem tenha sido esclarecido, os polinômios são adicionados seguindo estas etapas:
-Pedido Primeiramente os polinômios a serem somados, todos da mesma forma, seja de forma crescente ou decrescente, ou seja, com as potências de menor para maior ou vice-versa.
-Completar, no caso de faltar algum poder na sequência.
-Reduzir termos como.
-Indicar a soma resultante.
Índice do artigo
- 1 Exemplos de adição de polinômios
- 1.1 Adicionar dois ou mais polinômios com mais de uma variável
- 2 exercícios para adicionar polinômios
- 2.1 - Exercício 1
- 2.2 - Exercício 2
- 3 referências
Exemplos de adição de polinômios
Começaremos adicionando dois polinômios com uma única variável chamada x, por exemplo, os polinômios P (x) e Q (x) dados por:
P (x) = 2xdois - 5x4 + 2x -x5 - 3x3 +12
Q (x) = x5- 25 x + xdois
Seguindo as etapas descritas, você começa ordenando-as em ordem decrescente, que é a maneira mais comum:
P (x) = -x5- 5x4 - 3x3 + 2xdois + 2x +12
Q (x) = x5+ xdois - 25x
O polinômio Q (x) não está completo, vê-se que faltam potências com expoentes 4, 3 e 0. Este último é simplesmente o termo independente, aquele que não tem letra.
Q (x) = x5+ 0x4 + 0x3 + xdois - 25x + 0
Depois que essa etapa for concluída, eles estão prontos para adicionar. Você pode adicionar os termos semelhantes e, em seguida, indicar a soma, ou colocar os polinômios ordenados um abaixo do outro e reduzir por colunas, desta forma:
- x5 - 5x4 - 3x3 + 2xdois + 2x +12
+ x5 + 0x4 + 0x3 + xdois - 25x + 0 +
--
0x5-5x4 - 3x3 +3xdois - 23x + 12 = P (x) + Q (x)
É importante notar que quando adicionado, é feito algebricamente respeitando a regra dos sinais, desta forma 2x + (-25 x) = -23x. Ou seja, se os coeficientes têm um sinal diferente, eles são subtraídos e o resultado carrega o sinal do maior.
Adicione dois ou mais polinômios com mais de uma variável
Quando se trata de polinômios com mais de uma variável, escolhe-se uma delas para ordená-la. Por exemplo, suponha que você peça para adicionar:
R (x, y) = 5xdois - 4 anosdois + 8xy - 6y3
Y:
T (x, y) = ½ xdois- 6adois - 11xy + x3Y
Uma das variáveis é escolhida, por exemplo x para solicitar:
R (x, y) = 5xdois + 8xy - 6y3 - 4 anosdois
T (x, y) = + x3y + ½ xdois - 11xy - 6ydois
Imediatamente os termos ausentes são preenchidos, de acordo com os quais cada polinômio tem:
R (x, y) = 0x3y + 5xdois + 8xy - 6y3 - 4 anosdois
T (x, y) = + x3y + ½ xdois - 11xy + 0y3 - 6adois
E vocês dois estão prontos para reduzir termos semelhantes:
0x3y + 5xdois + 8xy - 6y3 - 4 anosdois
+ x3y + ½ xdois - 11xy + 0y3 - 6adois +
-
+ x3e + 11 / 2xdois - 3xy - 6y3 - 10adois = R (x, y) + T (x, y)
Exercícios de adição polinomial
- Exercício 1
Na seguinte soma de polinômios, indique o termo que deve ir no espaço em branco para obter a soma polinomial:
-5x4 + 0x3 + 2xdois + 1
x5 + 2x4 - 21xdois + 8x - 3
2x5 +9x3 -14x
-
-6x5+10x4 -0x3 + 5xdois - 11x + 21
Solução
Para obter -6x5 um termo da forma machado é necessário5, tal que:
a + 1+ 2 = -6
Portanto:
a = -6-1-2 = -9
E o termo de pesquisa é:
-9x5
-Proceda de maneira semelhante para localizar o restante dos termos. Aqui está aquele para o expoente 4:
-5 + 2 + a = 10 → a = 10 + 5-2 = 13
O termo ausente é: 13x4.
-Para as potências de x3 é imediato que o prazo deve ser -9x3, assim, o coeficiente do termo cúbico é 0.
-Em relação às potências quadradas: a + 8 - 14 = -11 → a = -11 - 8 + 14 = -5 e o termo é -5xdois.
-O termo linear é obtido por meio de a +8 -14 = -11 → a = -11 + 14 - 8 = -5, o termo ausente sendo -5x.
-Finalmente, o termo independente é: 1 -3 + a = -21 → a = -19.
- Exercício 2
Um terreno plano é cercado como mostrado na figura. Encontre uma expressão para:
a) O perímetro e
b) Sua área, nos comprimentos indicados:
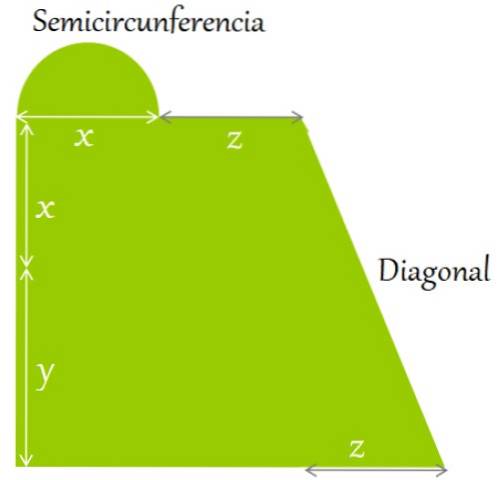
Solução para
O perímetro é definido como a soma dos lados e contornos da figura. Começando no canto inferior esquerdo, no sentido horário, temos:
Perímetro = y + x + comprimento do semicírculo + z + comprimento diagonal + z + z + x
O semicírculo tem um diâmetro igual a x. Como o raio é a metade do diâmetro, temos que:
Raio = x / 2.
A fórmula para o comprimento de uma circunferência completa é:
L = 2π x Raio
Então:
Comprimento do semicírculo = ½. 2π (x / 2) = πx / 2
Por sua vez, a diagonal é calculada com o teorema de Pitágoras aplicado aos lados: (x + y) que é o lado vertical ez, que é o horizontal:
Diagonal = [(x + y)dois + zdois]1/2
Estas expressões são substituídas na do perímetro, para obter:
Perímetro = y + x + πx / 2 + z + [(x + y)dois + zdois]1/2+ z + x + z
Termos semelhantes são reduzidos, uma vez que a adição exige que o resultado seja simplificado tanto quanto possível:
Perímetro = y + [x + π (x / 2) + x] + z + z + z + [(x + y)dois + zdois]1/2 = y + (2 + π / 2) x + 3z
Solução b
A área resultante é a soma da área do retângulo, do semicírculo e do triângulo retângulo. As fórmulas para essas áreas são:
-Retângulo: base x altura
-Semicírculo: ½ π (raio)dois
-Triângulo: base x altura / 2
Área retângulo
(x + y). (x + z) = xdois + xz + yx + yz
Área semicírculo
½ π (x / 2)dois = π xdois / 8
Área do triângulo
½ z (x + y) = ½ zx + ½ zy
Área total
Para encontrar a área total, são adicionadas as expressões encontradas para cada área parcial:
Área total = xdois + xz + yx + yz + (π xdois / 8) + ½ zx + ½ zy
E, finalmente, todos os termos semelhantes são reduzidos:
Área total = (1 + π / 8) xdois + 3/2 xy + 3 / 2yz + yx
Referências
- Baldor, A. 1991. Algebra. Editorial Cultural Venezolana S.A.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Math is Fun. Adicionando e subtraindo polinômios. Recuperado de: mathsisfun.com.
- Monterey Institute. Adicionando e subtraindo polinômios. Recuperado de: montereyinstitute.org.
- UC Berkeley. Álgebra de polinômios. Recuperado de: math.berkeley.edu.



Ainda sem comentários