
Riemann soma história, fórmulas e propriedades, exercícios
O Soma de Riemann é o nome dado ao cálculo aproximado de uma integral definida, por meio de uma soma discreta com um número finito de termos. Uma aplicação comum é a aproximação da área de funções em um gráfico.
Foi o matemático alemão Georg Friedrich Bernhard Riemann (1826-1866) quem primeiro ofereceu uma definição rigorosa da integral de uma função em um determinado intervalo. Ele tornou isso conhecido em um artigo publicado em 1854.
A soma de Riemann é definida em uma função y = f (x), com x pertencendo ao intervalo fechado [a, b]. Neste intervalo, uma partição P de n elementos é feita:
P = x0= a, x1, xdois,..., xn= b
Isso significa que o intervalo é dividido da seguinte forma:

xk-1 ≤ tk ≤ xk
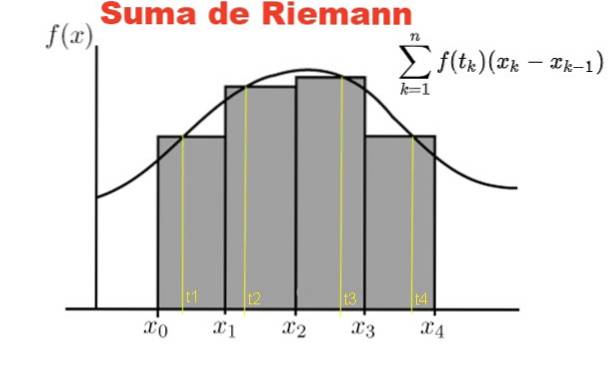
A Figura 1 mostra graficamente a soma de Riemann da função f no intervalo [x0, x4] em uma partição de quatro subintervalos, os retângulos cinza.
A soma representa a área total dos retângulos e o resultado dessa soma aproxima numericamente a área sob a curva f, entre as abcissas x = x0 y x = x4.
Claro, a aproximação da área sob a curva melhora muito à medida que o número n partições é maior. Desta forma, a soma converge para a área sob a curva, quando o número n de partições tende ao infinito.
Índice do artigo
- 1 Fórmulas e propriedades
- 1.1 A área sob a curva
- 2 exercícios resolvidos
- 2.1 - Exercício 1
- 2.2 - Exercício 2
- 3 referências
Fórmulas e propriedades
A soma de Riemann da função f (x) na partição:
P = x0= a, x1, xdois,..., xn= b
Definido no intervalo [a, b], é dado por:
S (P, f) = ∑k = 1n f (tk) (xk - xk-1)
Onde Tk é um valor no intervalo [xk, xk-1] Na soma de Riemann, intervalos regulares de largura Δx = (b - a) / n são normalmente usados, onde aeb são os valores mínimo e máximo da abcissa, enquanto n é o número de subdivisões.
Nesse caso, o Soma certa de Riemann isso é:
Sd (f, n) = [f (a + Δx) + f (a + 2Δx) +… + f (a + (n-1) Δx) + f (b)] * Δx
Enquanto o Riemann deixou a soma é expresso como:
Se (f, n) = [f (a) + f (a + Δx) +… + f (a + (n-1) Δx)] * Δx
Finalmente, o soma de Riemann central isso é:
Sc (f, n) = [f (a + Δx / 2) + f (a + 3Δx / 2) +… + f (b- Δx / 2)] * Δx
Dependendo de onde o ponto t está localizadok no intervalo [xk, xk-1] a soma de Riemann pode superestimar ou subestimar o valor exato da área sob a curva da função y = f (x). Em outras palavras, os retângulos podem se projetar da curva ou ficar um pouco abaixo dela..
A área sob a curva
A principal propriedade da soma de Riemann e da qual deriva sua importância, é que se o número de subdivisões tende ao infinito, o resultado da soma converge para a integral definida da função:

Exercícios resolvidos
- Exercício 1
Calcule o valor da integral definida entre a = -2 a b = +2 da função:
f (x) = xdois
Faça uso de uma soma de Riemann. Para fazer isso, primeiro encontre a soma para n partições regulares do intervalo [a, b] e, em seguida, tome o limite matemático para o caso em que o número de partições tende ao infinito.
Solução
Estas são as etapas a seguir:
-Primeiro, defina o intervalo das partições como:
Δx = (b - a) / n.
-Então, a soma de Riemann da direita correspondente à função f (x) fica assim:


[-2 + (4i / n)]dois = 4 - (16 i / n) + (4 / n)dois eudois
-E então é cuidadosamente substituído no somatório:

-O próximo passo é separar as somas e tomar as quantidades constantes como um fator comum de cada soma. É preciso levar em consideração que o índice é i, portanto os números e os termos com n são considerados constantes:

-Cada somatório é avaliado, pois para cada um deles existem expressões adequadas. Por exemplo, a primeira das somas dá n:



S (f, n) = 16 - 64 (n + 1) / 2n + 64 (n + 1) (2n + 1) / 6ndois
-Finalmente, temos que a integral que queremos calcular é:

= 16 - (64/2) + (64/3) = 16/3 = 5.333
O leitor pode verificar que este é o resultado exato, que pode ser obtido resolvendo a integral indefinida e avaliando os limites de integração pela regra de Barrow.
- Exercício 2
Determine aproximadamente a área sob a função:
f (x) = (1 / √ (2π)) e(-xdois/dois)
Insira x = -1 e x = + 1, usando uma soma de Riemann central com 10 partições. Compare com o resultado exato e estime a diferença percentual.
Solução
O passo ou incremento entre dois valores discretos sucessivos é:
Δx = (1 - (-1) / 10 = 0,2
Portanto, a partição P na qual os retângulos são definidos se parece com isto:
P = -1,0; -0,8; -0,6; -0,4; -0,2; 0,0; 0,2; 0,4; 0,6; 0,8; 1.0
Mas como o que se deseja é a soma central, a função f (x) será avaliada nos pontos médios dos subintervalos, ou seja, no conjunto:
T = -0,9; -0,7; -0,5; -0,3; -0,1; 0,1; 0,3; 0,5; 0,7; 0,9.
A soma de Riemann (central) é assim:
S = f (-0,9) * 0,2 + f (-0,7) * 0,2 + f (-0,5) * 0,2 +… + f (0,7) * 0,2 + f (0,9) * 0,2
Como a função f é simétrica, é possível reduzir a soma para apenas 5 termos e o resultado é multiplicado por dois:
S = 2 * 0,2 * f (0,1) + f (0,3) + f (0,5) + f (0,7) + f (0,9)
S = 2 * 0,2 * 0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683
A função dada neste exemplo não é outra senão o conhecido sino Gaussiano (normalizado, com média igual a zero e desvio padrão um). A área sob a curva no intervalo [-1,1] para esta função é conhecida como 0,6827.

Isso significa que a solução aproximada com apenas 10 termos corresponde à solução exata para três casas decimais. O erro percentual entre o integral aproximado e exato é 0,07%.
Referências
- Casteleiro, J. M., & Gómez-Álvarez, R. P. (2002). Cálculo integral (edição ilustrada). Madrid: Editorial ESIC.
- Unican. História do conceito de integral. Recuperado de: repositorio.unican.es
- UIS. Riemann soma. Recuperado de: matematicas.uis.edu.co
- Wikipedia. Soma de Riemann. Recuperado de: es.wikipedia.com
- Wikipedia. Integração de Riemann. Recuperado de: es.wikipedia.com



Ainda sem comentários