O teoria cinética molecular É aquele que procura explicar as observações experimentais de gases de uma perspectiva microscópica. Ou seja, tenta associar a natureza e o comportamento das partículas gasosas, com as características físicas do gás como fluido; explicar o macroscópico do microscópico.
Os gases sempre foram do interesse dos cientistas por causa de suas propriedades. Ocupam todo o volume do recipiente em que se encontram, podendo ser totalmente comprimidos sem que o seu conteúdo oponha a menor resistência; e se a temperatura aumentar, o recipiente começa a se expandir e pode até rachar.
Muitas dessas propriedades e comportamentos são resumidos nas leis dos gases ideais. No entanto, eles consideram o gás como um todo e não como uma coleção de milhões de partículas espalhadas no espaço; Além disso, não fornece, com base em dados de pressão, volume e temperatura, mais informações sobre como essas partículas se movem.
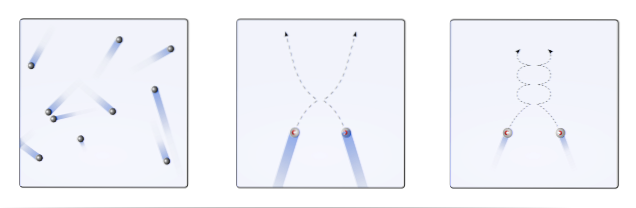
É assim que a teoria cinética molecular (TCM), se propõe a visualizá-los como esferas móveis (imagem superior). Essas esferas colidem entre si e com as paredes arbitrariamente e mantêm uma trajetória linear. No entanto, quando a temperatura diminui e a pressão aumenta, a trajetória das esferas torna-se curva..
Um gás, de acordo com TCM, deve se comportar como as esferas do primeiro quadro da imagem. Mas, ao esfriar e aumentar a pressão sobre eles, seu comportamento está longe do ideal. Eles são então gases reais, perto de sofrer liquefação e, assim, passam para a fase líquida.
Nessas condições, as interações entre as esferas tornam-se mais importantes, a ponto de suas velocidades diminuírem momentaneamente. Quanto mais próximos estão da liquefação, mais curvas suas trajetórias se tornam (inserção à direita) e menos energéticas suas colisões.
Índice do artigo
A ideia dessas esferas, melhor chamadas de átomos, já havia sido considerada pelo filósofo romano Lucrécio; não para gases, mas para objetos estáticos e sólidos. Por outro lado, em 1738 Daniel Bernoulli aplicou a visão atômica a gases e líquidos imaginando-os como esferas desordenadas movendo-se em todas as direções..
Seu trabalho, entretanto, violava as leis da física da época; um corpo não podia se mover eternamente, então era impossível pensar que um conjunto de átomos e moléculas colidiriam uns com os outros sem perder sua energia; ou seja, a existência de colisões elásticas não foi possível.
Um século depois, outros autores reforçaram o TCM com um modelo em que as partículas gasosas se moviam em apenas uma direção. Rudolf Clausius, no entanto, compilou seus resultados e montou um modelo TCM mais completo com o qual procurou explicar as leis dos gases ideais demonstradas por Boyle, Charles, Dalton e Avogadro..
Em 1859, James Clerk Maxwell afirmou que as partículas gasosas apresentam uma gama de velocidades a uma dada temperatura, e que um conjunto delas pode ser considerado por meio de uma velocidade molecular média..
Então, em 1871, Ludwig Boltzmann conectou as idéias existentes com a entropia, e como o gás termodinamicamente sempre tende a ocupar tanto espaço quanto possível de forma homogênea e espontânea.
Para considerar o gás de suas partículas, é necessário um modelo no qual certos postulados ou suposições sejam cumpridos; postula que logicamente deve ser capaz de prever e explicar (o mais precisamente possível) observações macroscópicas e experimentais. Dito isso, os postulados do TCM são mencionados e descritos.
Em um recipiente cheio de partículas gasosas, elas se dispersam e se afastam umas das outras em todos os cantos. Se por um momento eles pudessem ser reunidos em um ponto específico do recipiente, sem liquefação, seria observado que eles ocupam apenas uma parcela desprezível do volume do recipiente..
Isso significa que o recipiente, mesmo que contenha milhões de partículas gasosas, está na verdade mais vazio do que cheio (relação volume-vazio muito menor que 1); portanto, se suas barreiras permitirem, ele e o gás dentro dele podem ser comprimidos abruptamente; já que no final do dia as partículas são muito pequenas, assim como o seu volume.
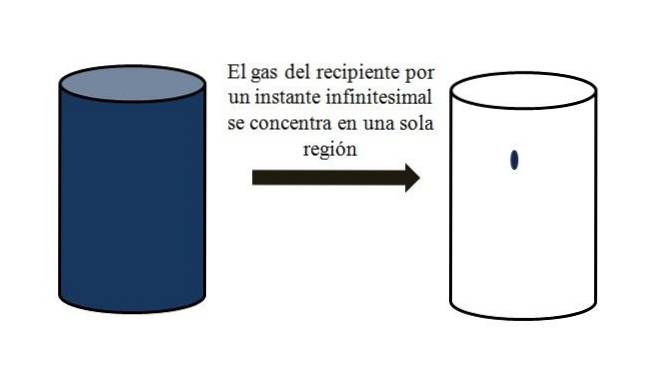
A imagem superior ilustra com precisão o acima, usando um gás de cor azulada.
As partículas gasosas dentro do recipiente colidem umas com as outras sem tempo suficiente para que suas interações ganhem força; menos ainda quando o que principalmente os rodeia é o vácuo molecular. Uma consequência imediata disso é que seus caminhos lineares permitem que eles abranjam completamente o volume do container..
Se assim não fosse, um recipiente com formato "bizarro" e "labiríntico" teria regiões úmidas em decorrência da condensação do gás; em vez disso, as partículas viajam ao redor do contêiner com total liberdade, sem que a força de suas interações as pare.
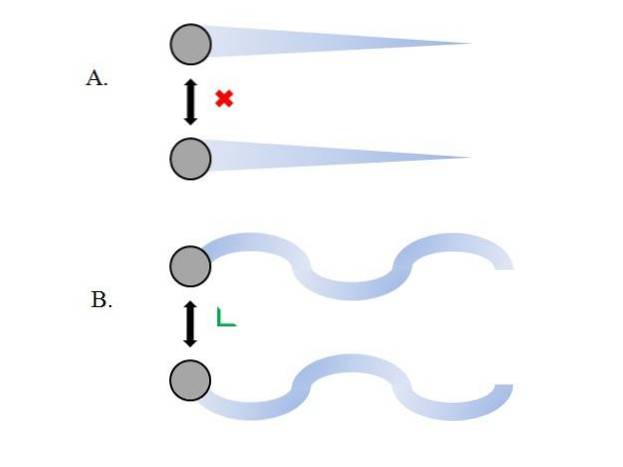
As trajetórias lineares da imagem superior (A.) demonstram este postulado; enquanto se as trajetórias são curvas (B.), isso mostra que existem interações que não podem ser ignoradas entre as partículas.
Dos dois primeiros postulados, o fato de que as partículas de gás nunca param de se mover também converge. Uma vez borrados no recipiente, colidem entre si e com suas paredes, com força e velocidade diretamente proporcionais à temperatura absoluta; esta força é pressão.
Se as partículas gasosas parassem de se mover por um instante, "línguas de fumaça" seriam testemunhadas dentro do recipiente, emergindo do nada, com tempo suficiente para se organizar no vácuo e dar formas aleatórias..
Se somente colisões elásticas entre as partículas gasosas e as paredes do recipiente predominam dentro do recipiente, a condensação do gás nunca ocorrerá (desde que as condições físicas não mudem); ou o que é o mesmo que dizer que nunca descansam e estão sempre colidindo.
Isso ocorre porque em colisões elásticas não há perda líquida de energia cinética; uma partícula colide com a parede e salta na mesma velocidade. Se uma partícula ao colidir desacelera, a outra acelera, sem produzir calor ou som que dissipa a energia cinética de qualquer uma delas.
O movimento das partículas é aleatório e caótico, de modo que nem todas têm a mesma velocidade; assim como acontece, por exemplo, em uma rodovia ou no meio de uma multidão. Alguns são mais enérgicos e viajam mais rápido, enquanto outros são lentos, esperando uma colisão para acelerá-los.
Para descrever sua velocidade, é necessário calcular uma média; e com isso, a energia cinética média das partículas ou moléculas gasosas é obtida por sua vez. Como a energia cinética de todas as partículas está em constante mudança, a média permite melhor controle dos dados e pode ser trabalhada com maior confiabilidade..
Energia cinética molecular média (ECmp) em um recipiente muda com a temperatura. Quanto mais alta a temperatura, maior será a energia. Por ser uma média, pode haver partículas ou gases com energia maior ou menor que esse valor; alguns mais rápidos e outros mais lentos, respectivamente.
Matematicamente, pode ser mostrado que ECmp depende exclusivamente da temperatura. Isso significa que não importa qual seja o gás, sua massa ou estrutura molecular, sua ECmp será o mesmo a uma temperatura T e só variará se aumentar ou diminuir. De todos os postulados, este talvez seja o mais relevante..
E a velocidade molecular média? Ao contrário de ECmp, a massa molecular influencia a velocidade. Quanto mais pesada a partícula ou molécula gasosa, é natural esperar que ela se mova mais lentamente..
Aqui estão alguns exemplos breves de como o TCM conseguiu explicar as leis dos gases ideais. Embora não sejam abordados, outros fenômenos, como difusão e efusão de gás, também podem ser explicados com TCM.
Se o volume do recipiente for comprimido a temperatura constante, a distância que as partículas gasosas devem percorrer para colidir com as paredes diminui; que é igual a um aumento na frequência de tais colisões, resultando em maior pressão. Como a temperatura permanece constante, ECmp também é constante.
Se você aumentar T, ECmp vai aumentar. As partículas gasosas irão se mover mais rápido e colidir um número maior de vezes com as paredes do recipiente; então a pressão aumenta.
Se as paredes forem flexíveis, capazes de se expandir, sua área ficará maior e a pressão cairá até se tornar constante; e, como resultado, o volume também aumentará.
Se vários litros de gases diferentes fossem adicionados a um recipiente espaçoso, vindos de recipientes menores, sua pressão interna total seria igual à soma das pressões parciais exercidas por cada tipo de gás separadamente..
Por quê? Porque todos os gases começam a colidir uns com os outros e se dispersar homogeneamente; as interações entre eles são nulas, e o vácuo predomina no recipiente (postulados do TCM), então é como se cada gás estivesse sozinho, exercendo sua pressão individualmente sem a interferência dos demais gases..
Ainda sem comentários