
Equação do teorema de Bernoulli, aplicações e exercício resolvido
O Teorema de Bernoulli, que descreve o comportamento de um líquido em movimento, foi enunciada pelo matemático e físico Daniel Bernoulli em sua obra Hidrodinâmica. De acordo com o princípio, um fluido ideal (sem atrito ou viscosidade) que esteja circulando por um conduíte fechado, terá uma energia constante em seu caminho.
O teorema pode ser deduzido do princípio da conservação da energia e até mesmo da segunda lei do movimento de Newton. Além disso, o princípio de Bernoulli também estabelece que um aumento na velocidade de um fluido implica uma diminuição da pressão a que está sujeito, uma diminuição de sua energia potencial, ou ambos ao mesmo tempo..

O teorema tem muitas aplicações diferentes, tanto no mundo da ciência quanto na vida cotidiana das pessoas..
Suas consequências estão presentes na força de sustentação de aviões, nas chaminés de residências e indústrias, nas tubulações de água, entre outras áreas..
Índice do artigo
- 1 equação de Bernoulli
- 1.1 Forma simplificada
- 2 inscrições
- 3 Exercício resolvido
- 4 referências
Equação de Bernoulli
Embora Bernoulli tenha deduzido que a pressão diminui quando a velocidade do fluxo aumenta, a verdade é que foi Leonhard Euler quem realmente desenvolveu a equação de Bernoulli na forma em que é conhecida hoje..
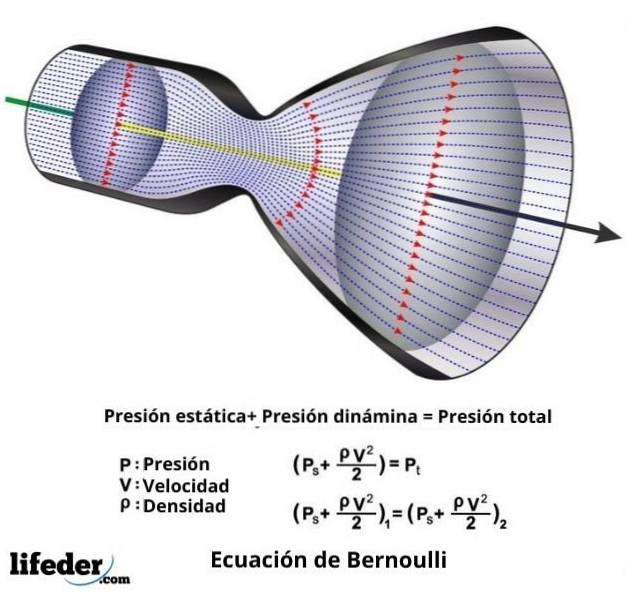
Em qualquer caso, a equação de Bernoulli, que nada mais é do que a expressão matemática de seu teorema, é a seguinte:
vdois ∙ ƿ / 2 + P + ƿ ∙ g ∙ z = constante
Nesta expressão, v é a velocidade do fluido através da seção considerada, ƿ é a densidade do fluido, P é a pressão do fluido, g é o valor da aceleração da gravidade e z é a altura medida no direção da gravidade.
Está implícito na equação de Bernoulli que a energia de um fluido consiste em três componentes:
- Um componente cinético, que é aquele que resulta da velocidade com que o fluido se move.
- Um componente potencial ou gravitacional, que é devido à altura em que o fluido está.
- Uma energia de pressão, que é aquela que o fluido possui em consequência da pressão a que está sujeito.
Por outro lado, a equação de Bernoulli também pode ser expressa assim:
v1 dois ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vdoisdois ∙ ƿ / 2 + Pdois + ƿ ∙ g ∙ zdois
Esta última expressão é muito prática para analisar as mudanças que um fluido experimenta quando algum dos elementos que compõem a equação muda..
Formulário simplificado
Em certas ocasiões, a mudança no termo ρgz da equação de Bernoulli é mínima em comparação com aquela experimentada pelos outros termos, portanto, pode ser negligenciada. Por exemplo, isso acontece em correntes experimentadas por um avião em vôo..

Nessas ocasiões, a equação de Bernoulli é expressa da seguinte forma:
P + q = P0
Nesta expressão, q é a pressão dinâmica e é equivalente av dois ∙ ƿ / 2 e P0 é o que é chamado de pressão total e é a soma da pressão estática P e da pressão dinâmica q.
Formulários

O teorema de Bernoulli tem muitas e diversas aplicações em campos tão diversos como ciência, engenharia, esportes, etc..
Uma aplicação interessante é encontrada no design de lareiras. As chaminés são construídas em altura de modo a conseguir uma maior diferença de pressão entre a base e a saída da chaminé, graças à qual é mais fácil extrair os gases de combustão.
Claro, a equação de Bernoulli também se aplica ao estudo do movimento dos fluxos de líquidos em tubos. Da equação segue-se que uma redução na área da seção transversal do tubo, a fim de aumentar a velocidade do fluido que passa por ele, também implica uma diminuição da pressão.
A equação de Bernoulli também é usada na aviação e em veículos de Fórmula 1. No caso da aviação, o efeito Bernoulli é a origem da sustentação dos aviões.
As asas da aeronave são projetadas com o objetivo de obter maior fluxo de ar na parte superior da asa.
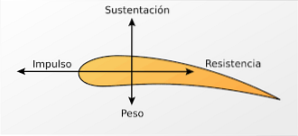
Assim, na parte superior da asa a velocidade do ar é alta e, portanto, a pressão é menor. Essa diferença de pressão produz uma força dirigida verticalmente para cima (força de sustentação) que permite que a aeronave flutue no ar. Um efeito semelhante é obtido nos ailerons dos carros de Fórmula 1.
Exercício resolvido
Através de um tubo com seção transversal de 4,2 cmdois um fluxo de água corre a 5,18 m / s. A água desce de uma altura de 9,66 m para um nível inferior com uma altura de elevação zero, enquanto a área da seção transversal do tubo aumenta para 7,6 cmdois.
a) Calcule a velocidade da corrente de água no nível inferior.
b) Determine a pressão no nível inferior sabendo que a pressão no nível superior é 152000 Pa.
Solução
a) Dado que o fluxo deve ser conservado, é verdade que:
Qnivel superior = Qnível mais baixo
v1 . S1 = vdois . Sdois
5,18 m / s. 4,2 cmdois = vdois . 7,6 cm ^dois
Resolvendo para, obtém-se que:
vdois = 2,86 m / s
b) Aplicando o teorema de Bernoulli entre os dois níveis, e levando em consideração que a densidade da água é 1000 kg / m3 , obtém-se que:
v1 dois ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vdoisdois ∙ ƿ / 2 + Pdois + ƿ ∙ g ∙ zdois
(1/2). 1000 kg / m3 . (5,18 m / s)dois + 152000 + 1000 kg / m3 . 10 m / sdois . 9,66 m =
= (1/2). 1000 kg / m3 . (2,86 m / s)dois + Pdois + 1000 kg / m3 . 10 m / sdois . 0 m
Resolvendo para Pdois se chega a:
Pdois = 257926,4 Pa
Referências
- Princípio de Bernoulli. (WL.). Na Wikipedia. Obtido em 12 de maio de 2018, em es.wikipedia.org.
- Princípio de Bernoulli. (WL.). Na Wikipedia. Obtido em 12 de maio de 2018 em en.wikipedia.org.
- Batchelor, G.K. (1967). Uma introdução à dinâmica dos fluidos. Cambridge University Press.
- Lamb, H. (1993). Hidrodinâmica (6ª ed.). Cambridge University Press.
- Mott, Robert (1996). Mecânica de fluidos aplicada (4ª ed.). México: Pearson Education.



Ainda sem comentários