
Prova, exemplos e exercícios do teorema de existência e exclusividade
O Teorema de existência e unicidade estabelece as condições necessárias e suficientes para que uma equação diferencial de primeira ordem, com uma dada condição inicial, tenha uma solução e que esta solução seja também a única.
No entanto, o teorema não fornece nenhuma técnica ou indicação de como encontrar tal solução. O teorema de existência e unicidade também é estendido para equações diferenciais de ordem superior com condições iniciais, que é conhecido como o problema de Cauchy..
A declaração formal do teorema de existência e unicidade é a seguinte:
"Para uma equação diferencial y '(x) = f (x, y) com condição inicial y (a) = b, existe pelo menos uma solução em uma região retangular do plano XY contendo ao ponto (a, b), sim f (x, y) é contínuo naquela região. E se a derivada parcial de F em relação à Y: g = ∂f / ∂e é contínua nessa mesma região retangular, então a solução é única em uma vizinhança do ponto (a, b) conteúdo na região de continuidade de F Y g."
A utilidade deste teorema está em primeiro lugar em saber quais são as regiões do plano XY em que pode existir uma solução e também em saber se a solução encontrada é a única possível ou se existem outras..
Observe que, caso a condição de unicidade não seja satisfeita, o teorema não pode prever quantas soluções no total o problema de Cauchy tem: talvez seja uma, duas ou mais.
Índice do artigo
- 1 Prova da existência e teorema da unicidade
- 2 exemplos
- 2.1 - Exemplo 1
- 2.2 - Exemplo 2
- 3 exercícios resolvidos
- 3.1 - Exercício 1
- 3.2 - Exercício 2
- 4 referências
Prova da existência e teorema da unicidade

Para este teorema, são conhecidas duas provas possíveis, uma delas é a prova de Charles Émile Picard (1856-1941) e a outra é devida a Giuseppe Peano (1858-1932) com base nas obras de Augustin Louis Cauchy (1789-1857 ).
Vale ressaltar que as mais brilhantes mentes matemáticas do século XIX participaram da prova desse teorema, portanto, pode-se intuir que nenhum dos dois é simples..
Para provar formalmente o teorema, é necessário primeiro estabelecer uma série de conceitos matemáticos mais avançados, como funções do tipo Lipschitz, espaços de Banach, teorema da existência de Carathéodory e vários outros, que estão além do escopo do artigo..
Grande parte das equações diferenciais que são tratadas em física lida com funções contínuas nas regiões de interesse, portanto, nos limitaremos a mostrar como o teorema é aplicado em equações simples..
Exemplos
- Exemplo 1
Vamos considerar a seguinte equação diferencial com uma condição inicial:
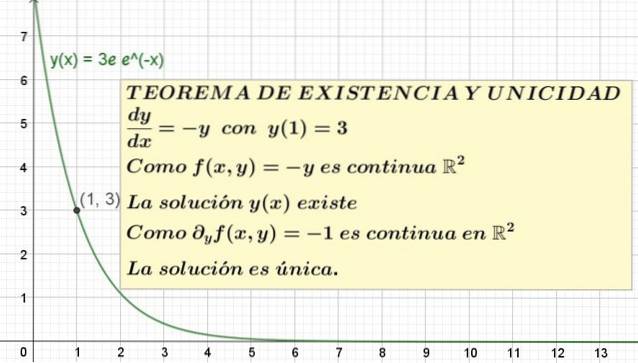
y '(x) = - y; com y (1) = 3
Existe uma solução para este problema? É a única solução possível?
Respostas
Em primeiro lugar, avalia-se a existência da solução da equação diferencial e que também cumpre a condição inicial.
Neste exemplo f (x, y) = - y a condição de existência requer saber se f (x, y) é contínuo em uma região do plano XY que contém o ponto das coordenadas x = 1, y = 3.
Mas f (x, y) = - y é o função afim, que é contínuo no domínio dos números reais e existe em toda a gama dos números reais.
Portanto, conclui-se que f (x, y) é contínua em Rdois, então o teorema garante a existência de pelo menos uma solução.
Sabendo disso, é necessário avaliar se a solução é única ou se, ao contrário, existe mais de uma. Para isso é necessário calcular a derivada parcial de F com respeito à variável Y:
∂f / ∂y = ∂ (-y) / ∂y = -1
Então g (x, y) = -1 que é uma função constante, que também é definida para todos os Rdois e também é contínuo lá. Segue-se que o teorema da existência e da unicidade garante que esse problema de valor inicial tenha uma solução única, embora não nos diga qual é..
- Exemplo 2
Considere a seguinte equação diferencial ordinária de primeira ordem com a condição inicial:
y '(x) = 2√y; y (0) = 0.
Há uma solução y (x) para este problema? Em caso afirmativo, determine se há um ou mais de um.
Responder
Nós consideramos a função f (x, y) = 2√y. A função F é definido apenas para y≥0, já que sabemos que um número negativo carece de uma raiz real. O que mais f (x, y) é contínuo na metade superior do plano de Rdois incluindo o eixo X, então o teorema de existência e unicidade garante pelo menos uma solução nessa região.
Agora, a condição inicial x = 0, y = 0 está na borda da região de solução. Em seguida, tomamos a derivada parcial de f (x, y) em relação a y:
∂f/ ∂y = 1 / √y
Neste caso, a função não é definida para y = 0, precisamente onde a condição inicial é.
O que o teorema nos diz? Diz-nos que embora saibamos que existe pelo menos uma solução, a metade superior do plano do eixo X incluindo o eixo X, uma vez que a condição de exclusividade não é satisfeita, não há garantia de que haverá uma solução única.
Isso significa que pode haver uma ou mais soluções na região de continuidade de f (x, y). E como sempre, o teorema não nos diz o que eles poderiam ser.
Exercícios resolvidos
- Exercício 1
Resolva o problema de Cauchy no Exemplo 1:
y '(x) = - y; com y (1) = 3.
Encontre a função y (x) que satisfaça a equação diferencial e a condição inicial.
Solução
No Exemplo 1 foi determinado que este problema tem solução e também é único. Para encontrar a solução, a primeira coisa a notar é que é uma equação diferencial do primeiro grau de variáveis separáveis, que é escrita da seguinte forma:
dy / dx = - y → dy = -y dx
Dividindo entre e em ambos os membros para separar as variáveis que temos:
dy / y = - dx
A integral indefinida é aplicada em ambos os membros:
∫ (1 / y) dy = - ∫dx
Resolvendo as integrais indefinidas, temos:
ln (y) = -x + C
onde C é uma constante de integração que é determinada pela condição inicial:
ln (3) = -1 + C, ou seja, C = 1 + ln (3)
Substituindo o valor de C e reorganizando-o permanece:
ln (y) - ln (3) = -x + 1
Aplicando a seguinte propriedade de logaritmos:
A diferença dos logaritmos é o logaritmo do quociente
A expressão acima pode ser reescrita assim:
ln (y / 3) = 1 - x
A função exponencial com base e em ambos os membros é aplicada para obter:
y / 3 = e(1 - x)
O que é equivalente a:
y = 3e e-x
Esta é a única solução da equação y '= -y com y (1) = 3. O gráfico desta solução é mostrado na figura 1.
- Exercício 2
Encontre duas soluções para o problema apresentado no Exemplo 2:
y '(x) = 2√ (y); y (0) = 0.
Solução
É também uma equação de variáveis separáveis, que, escrita na forma diferencial, tem a seguinte aparência:
dy / √ (y) = 2 dx
Tomando a integral indefinida em ambos os membros permanece:
dois √ (y) = 2 x + C
Como você sabe disso y≥0 na região de solução, temos:
y = (x + C)dois
Mas, uma vez que a condição inicial x = 0, y = 0 deve ser satisfeita, então a constante C é zero e a seguinte solução permanece:
y (x) = xdois.
Mas esta solução não é única, a função y (x) = 0 também é uma solução para o problema proposto. O teorema de existência e unicidade aplicado a este problema no Exemplo 2 já havia previsto que poderia haver mais de uma solução.
Referências
- Coddington, Earl A .; Levinson, Norman (1955), Theory of Ordinary Differential Equations, New York: McGraw-Hill.
- Enciclopédia de Matemática. Teorema de Cauchy-Lipschitz. Recuperado de: encyclopediaofmath.org
- Lindelöf, Sur l'application de la méthode des aproximations successives aux équations différentielles ordinaires du premier ordre; Comptes rendus hebdomadaires des séances de l'Académie des sciences. Vol. 116, 1894, pp. 454-457. Recuperado de: gallica.bnf.fr.
- Wikipedia. Método de aproximação sucessiva de Picard. Recuperado de: es.wikipedia.com
- Wikipedia. Teorema de Picard-Lindelöf. Recuperado de: es.wikipedia.com.
- Zill, D. 1986. Equações diferenciais elementares com aplicativos..


Ainda sem comentários