
Teorema de Green, prova, aplicações e exercícios
O Teorema de Green é um método de cálculo usado para relacionar integrais de linha a áreas duplas ou integrais de superfície. As funções envolvidas devem ser denotadas como campos vetoriais e definidas no caminho C.
Por exemplo, uma expressão integral de linha pode ser muito difícil de resolver; entretanto, ao implementar o teorema de Green, as integrais duplas se tornam bastante básicas. É sempre importante respeitar a direção positiva da trajetória, esta se refere ao sentido anti-horário.

O teorema de Green é um caso particular do teorema de Stokes, onde a projeção da função vetorial é realizada no plano xy.
Índice do artigo
- 1 definição
- 2 demo
- 3 aplicativos
- 4 História
- 5 Relação com outros teoremas
- 6 exercícios
- 7 referências
Definição
A expressão do Teorema de Green é a seguinte:
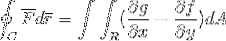
O primeiro termo mostra a integral de linha definida pelo caminho “C”, do produto escalar entre a função vetorial “F” e aquela do vetor “r”.
C: É o caminho definido no qual a função vetorial será projetada, desde que seja definida para aquele plano.
F: função vetorial, onde cada um de seus componentes é definido por uma função como (f, g).
r: É um vetor tangente à região R sobre a qual a integral é definida. Neste caso operamos com um diferencial deste vetor.
No segundo termo vemos desenvolvido o teorema de Green, onde se observa a integral dupla definida na região R da diferença das derivadas parciais de ge f, em relação a xey respectivamente. Por um diferencial de área que nada mais é do que o produto de ambos os diferenciais bidimensionais (dx.dy).
Este teorema é perfeitamente aplicável para integrais de espaço e superfície.
Demonstração
Para provar o teorema de Green de forma simples, esta tarefa será dividida em 2 partes. Primeiro, vamos assumir que a função vetorial F só tem definição no versor eu. Enquanto a função "g" correspondente ao versor j será igual a zero.
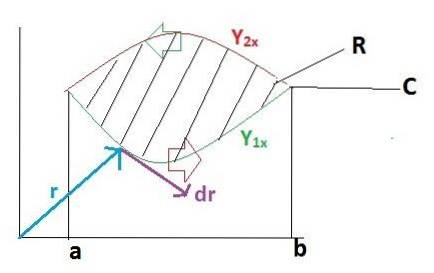
F = f (x, y)eu + g (x, y)j = f (x, y)eu + 0
r = xeu + Yj
dr = dxeu + tingirj
Primeiro, desenvolvemos a integral de linha ao longo da trajetória C, para a qual a trajetória foi setorizada em 2 seções que vão primeiro de a para be depois de b para a.
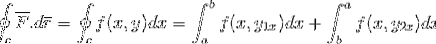
A definição do teorema fundamental do cálculo é aplicada para uma integral definida.
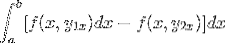
A expressão é reordenada em uma única integral, o negativo torna-se um fator comum e a ordem dos fatores é invertida.
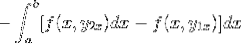
Ao observar esta expressão em detalhe, torna-se evidente que ao aplicar os critérios da função primitiva, estamos na presença da integral da expressão derivada de f em relação a y. Avaliado em parâmetros
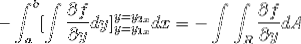
Agora é suficiente supor que a função vetorial F é definida apenas para g (x, y)j. Onde, quando operando de maneira semelhante ao caso anterior, o seguinte é obtido:
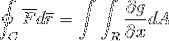
Para finalizar, as 2 provas são tomadas e unidas no caso em que a função vetorial assume valores para ambos os versores. Desta forma, mostra-se como a integral de linha após ser definida e considerada como uma trajetória unidimensional, pode ser totalmente desenvolvida para o plano e espaço..
F = f (x, y)eu + g (x, y)j
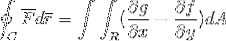
Desta forma, o teorema de Green é provado.
Formulários
As aplicações do teorema de Green são amplas nos ramos da física e da matemática. Eles se estendem a qualquer aplicação ou uso que possa ser dado à integração de linha.
O trabalho mecânico realizado por uma força F através de um caminho C, pode ser desenvolvido por uma integral de linha que é expressa como uma integral dupla de uma área por meio do teorema de Green..
Os momentos de inércia de muitos corpos sujeitos a forças externas em diferentes pontos de aplicação também respondem às integrais de linha que podem ser desenvolvidas com o teorema de Green..
Este possui múltiplas funcionalidades nos estudos de resistência dos materiais em uso. Onde os valores externos podem ser quantificados e levados em consideração antes da elaboração de vários elementos.
Em geral, o teorema de Green facilita a compreensão e definição das áreas onde as funções vetoriais são definidas em relação a uma região de acordo com uma trajetória.
História
Foi publicado em 1828 na obra Análise matemática às teorias de eletricidade e magnetismo, escrito pelo matemático britânico George Green. Nele, são exploradas seções bastante decisivas na aplicação do cálculo em física, como o conceito de funções potenciais, as funções de Green e as aplicações de seu teorema autointitulado..
George Green formalizou sua carreira de estudante aos 40 anos, sendo até agora um matemático totalmente autodidata. Depois de estudar na Universidade de Cambridge, ele continuou suas pesquisas, fazendo contribuições em acústica, ótica e hidrodinâmica que são válidas até hoje..
Relação com outros teoremas
O teorema de Green é um caso especial e surge de 2 outros teoremas muito importantes no campo do cálculo. Estes são o teorema de Kelvin-Stokes e o teorema da divergência ou Gauss Ostrogradski.
Partindo de qualquer um dos dois teoremas, é possível chegar ao teorema de Green. Certas definições e proposições são necessárias para desenvolver tais provas..
Treinamento
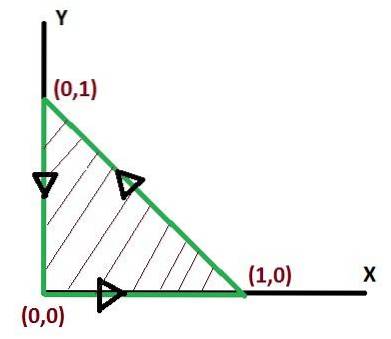
- O exercício a seguir mostra como transformar uma integral de linha em uma integral dupla em relação a uma região R.
A expressão original é a seguinte:
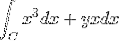
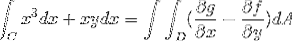
De onde as funções correspondentes af e g são retiradas
f (x, y) = x3 g (x, y) = yx
df / dy = 0 dg / dx = y
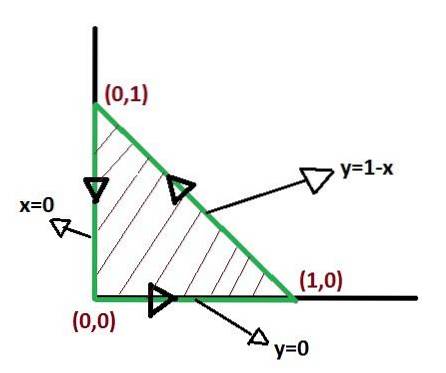
Não há uma maneira única de definir os limites da integração ao aplicar o teorema de Green. Mas existem maneiras em que as integrais após serem definidas podem ser mais simples. Portanto, a otimização dos limites de integração merece atenção.
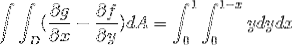
Onde, ao resolver as integrais, obtemos:
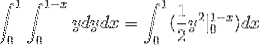
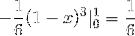
Este valor corresponde em unidades cúbicas à região abaixo da função vetorial e sobre a região triangular definida por C.
Para o caso da integral de linha sem realizar o método de Green, teria sido necessário parametrizar as funções em cada seção da região. Ou seja, execute 3 integrais parametrizados para a resolução. Esta é uma evidência suficiente da eficácia que Robert Green trouxe com seu teorema para o cálculo.
Referências
- Introdução à Mecânica do Contínuo. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23 de julho. 2009
- Cálculo multivariável. James Stewart. Cengage Learning, 22 de março 2011
- Uma história informal do teorema de Green e ideias associadas. James Joseph Cross. Departamento de Matemática, Universidade de Melbourne, 1975
- Condução de calor usando funções verdes. Kevin D. Cole, James V. Beck, A. Haji-Sheikh, Bahman Litkouhi. Taylor e Francis, 16 de julho 2010
- Aplicação do Teorema de Green à Extremização de Integrais Lineares. Centro de Informações Técnicas de Defesa, 1961


Ainda sem comentários