
Descrição do teorema de Norton, aplicações, exemplos e exercícios
O Teorema de Norton, que é aplicado a circuitos elétricos, estabelece que um circuito linear com dois terminais aeb, pode ser substituído por um completamente equivalente, que consiste em uma fonte de corrente denominada INão conectado em paralelo com um resistor RNão.
Disse eu atualNão ouviN É aquele que fluiria entre os pontos a e b, se estivessem em curto-circuito. A resistência RN é a resistência equivalente entre os terminais, quando todas as fontes independentes desligam. Tudo o que foi dito está delineado na figura 1.

A caixa preta na figura contém o circuito linear a ser substituído por seu equivalente Norton. Um circuito linear é aquele em que a entrada e a saída têm dependência linear, como a relação entre a tensão V e a corrente contínua I em um elemento ôhmico: V = I.R.
Esta expressão corresponde à lei de Ohm, onde R é a resistência, que também pode ser uma impedância, se for um circuito de corrente alternada.
O teorema de Norton foi desenvolvido pelo engenheiro elétrico e inventor Edward L. Norton (1898-1983), que trabalhou por muito tempo para a Bell Labs..
Índice do artigo
- 1 Aplicações do teorema de Norton
- 1.1 Relação entre os teoremas de Norton e Thevenin
- 2 exemplo
- 3 Exercício resolvido
- 4 referências
Aplicações do teorema de Norton
Quando você tem redes muito complicadas, com muitas resistências ou impedâncias e deseja calcular a tensão entre qualquer uma delas, ou a corrente que flui por ela, o teorema de Norton simplifica os cálculos, pois como vimos, a rede pode ser substituída por um circuito menor e mais gerenciável.
Desta forma, o teorema de Norton é muito importante ao projetar circuitos com múltiplos elementos, bem como estudar sua resposta..
Relação entre os teoremas de Norton e Thevenin
O teorema de Norton é o dual do teorema de Thevenin, o que significa que eles são equivalentes. O teorema de Thevenin indica que a caixa preta na figura 1 pode ser substituída por uma fonte de tensão em série com um resistor, chamada de resistência de Thevenin Rº. Isso é expresso na seguinte figura:
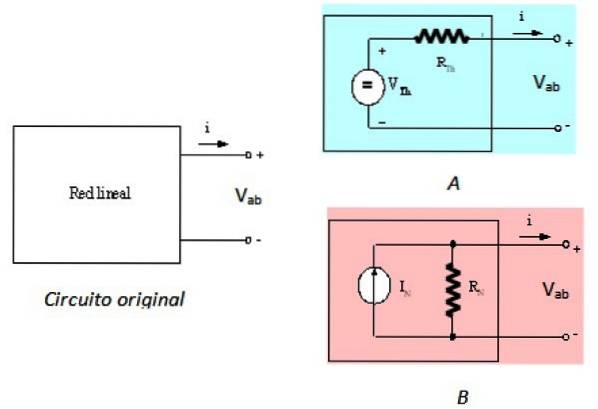
O circuito à esquerda é o circuito original, a rede linear na caixa preta, o circuito A no canto superior direito é o equivalente de Thevenin, e o circuito B é o equivalente do Norton, conforme descrito. Visto dos terminais aeb, os três circuitos são equivalentes.
Agora observe que:
-No circuito original, a tensão entre os terminais é Vab.
-Vab = Vº no circuito PARA
-Finalmente, Vab = EuN.RN no circuito B
Se os terminais aeb estiverem em curto-circuito em todos os três circuitos, deve-se garantir que a tensão e a corrente entre esses pontos sejam iguais para todos os três, uma vez que são equivalentes. Então:
-No circuito original a corrente é i.
-Para o circuito A, a corrente é i = Vº / Rº, de acordo com a lei de Ohm.
-Finalmente, no circuito B, a corrente é IN
Portanto, conclui-se que as resistências de Norton e Thevenin têm o mesmo valor, e que a corrente é dada por:
i = euN = Vº / Rº = Vº / RN
Exemplo
Para aplicar corretamente o teorema de Norton, as seguintes etapas são seguidas:
-Isole da rede a seção do circuito para a qual o equivalente Norton deve ser encontrado.
-No circuito restante, indique os terminais a e b.
-Substitua as fontes de tensão por curto-circuitos e as fontes de corrente por circuitos abertos, para encontrar a resistência equivalente entre os terminais a e b. Este é RN.
-Retorne todas as fontes às suas posições originais, curto-circuite os terminais a e b, e encontre a corrente que flui entre eles. Este sou euN.
-Desenhe o circuito equivalente de Norton de acordo com o que é indicado na figura 1. Tanto a fonte de corrente quanto a resistência equivalente estão em paralelo.
Você também pode aplicar o teorema de Thevenin para encontrar Rº, que já sabemos é igual a RN, então pela lei de Ohm você pode encontrar euN e prossiga para desenhar o circuito resultante.
E agora vamos ver um exemplo:
Encontre o Norton equivalente entre os pontos A e B do seguinte circuito:
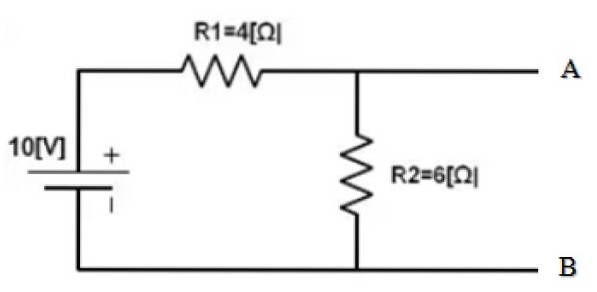
A parte do circuito cujo equivalente se encontra já está isolada. E os pontos A e B são claramente determinados. O seguinte é fazer um curto-circuito na fonte de 10 V e encontrar a resistência equivalente do circuito obtido:
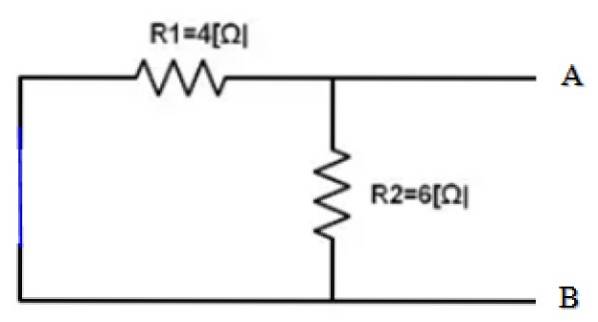
Vistas dos terminais A e B, ambos os resistores R1 e Rdois estão em paralelo, portanto:
1 / Req = 1 / R12 = (1/4) + (1/6) Ω-1 = 5/12 Ω-1 → Req = 12/5 Ω = 2,4 Ω
Em seguida, a fonte é devolvida ao seu lugar e os pontos A e B são curto-circuitados para encontrar a corrente que circula ali, esta será IN. Em tal caso:
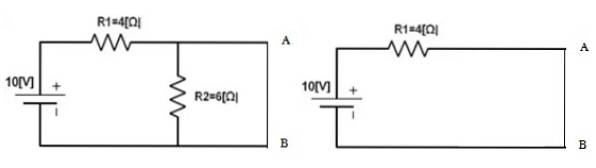
euN = 10 V / 4 Ω = 2,5 A
Equivalente de Norton
Finalmente, o equivalente do Norton é desenhado com os valores encontrados:
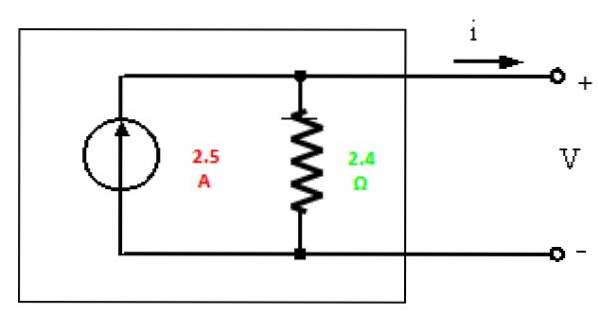
Exercício resolvido
No circuito da seguinte figura:
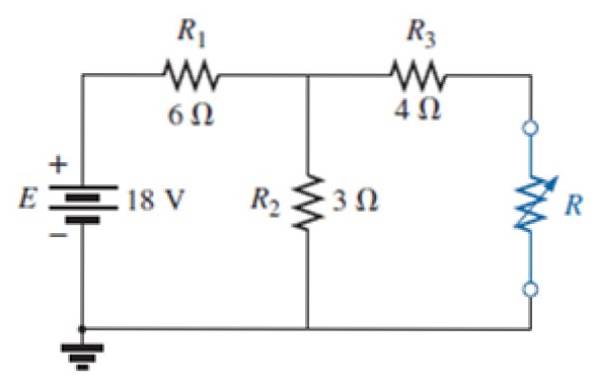
a) Encontre o circuito Norton equivalente da rede externa para o resistor azul.
b) Encontre também o equivalente Thévenin.
Solução para
Seguindo as etapas indicadas acima, a fonte deve ser curto-circuitada:
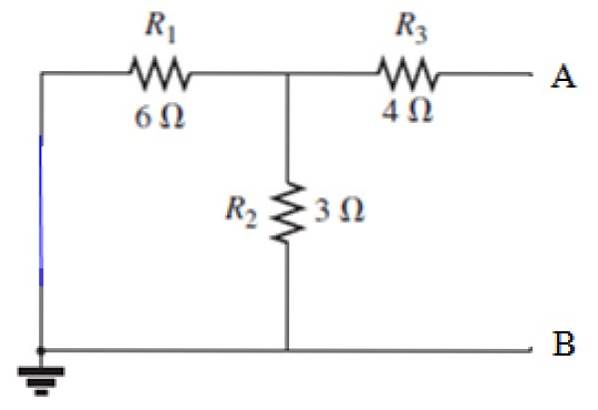
Cálculo de RN
Vista dos terminais A e B, resistor R3 está em série com o paralelo formado pelos resistores R1 e Rdois, vamos primeiro calcular a resistência equivalente deste paralelo:
1 / R12 = (1/6) + (1/3) Ω-1 = 1/2 Ω-1 → Req = 2/1 Ω = 2Ω
E então esse paralelo está em série com R3, de modo que a resistência equivalente é:
Req = 2 Ω + 4 Ω = 6 Ω
Este é o valor de ambos RN a partir de Rº, como explicado antes.
Cálculo IN
Os terminais A e B são então curto-circuitados, retornando a fonte ao seu lugar:
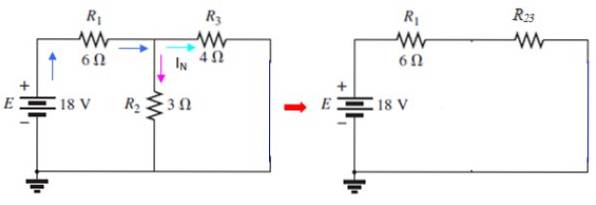
A corrente através de I3 é o atual euN procurado, que pode ser determinado usando o método da malha ou usando séries e paralelas. Neste circuito Rdois e R3 estão em paralelo:
1 / R2,3 = (1/3) + (1/4) Ω-1 = 7/12 Ω-1 → R2,3 = 12/7 Ω
A resistência R1 está em série com este paralelo, então:
R123 = 6 + (12/7) Ω = 54/7 Ω
A corrente que sai da fonte (cor azul) é calculada usando a lei de Ohm:
V = I. R → I = V / R = 18 V / (54/7 Ω) = 7/3 A
Esta corrente é dividida em duas partes: uma que passa por Rdois e outro que cruza R3. No entanto, a corrente através do paralelo R2,3 é o mesmo que passa por R1, como visto no circuito intermediário na figura. A tensão lá é:
V2,3 = I.R2,3 = (7/3) A. (12/7) Ω = 4 V
Ambos os resistores Rdois e R3 estão nessa tensão, uma vez que estão em paralelo, portanto:
eu3 = V2,3 / R3 = 4 V / 4 Ω = 1 A
Já temos a corrente Norton procurada, pois como disse anteriormente I3 = EuN, então:
euN = 1 A
Equivalente de Norton
Tudo está pronto para desenhar o equivalente Norton deste circuito entre os pontos A e B:
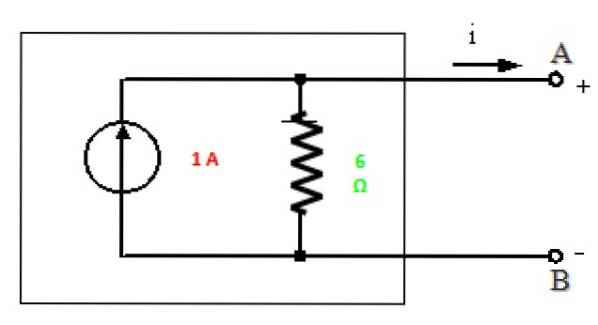
Solução b
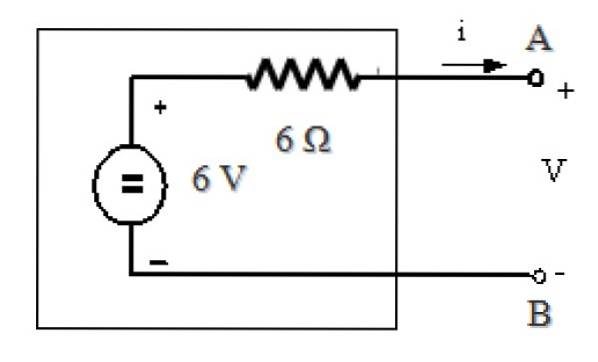
Encontrar o equivalente Thévenin é muito simples, pois Rº = RN= 6 Ω e conforme explicado nas seções anteriores:
Vº = EuN. RN = 1 A. 6 Ω = 6 V
O circuito equivalente Thévenin é:
Referências
- Alexander, C. 2006. Fundamentals of Electrical Circuits. 3º. Edição. Mc Graw Hill.
- Boylestad, R. 2011. Introdução à Análise de Circuito. 2ª Edição. Pearson.
- Dorf, R. 2006. Introdução aos circuitos elétricos. 7º. Edição. John Wiley & Sons.
- Edminister, J. 1996. Electrical Circuits. Schaum series. 3º. Edição. Mc Graw Hill.
- Wikipedia. Teorema de Norton. Recuperado de: es.wikipedia.org.


Ainda sem comentários