
Teorema de Thévenin em que consiste, aplicações e exemplos
O Teorema de Thévenin afirma que um circuito com terminais A e B pode ser substituído por um equivalente consistindo em uma fonte e uma resistência em série, cujos valores dão a mesma diferença de potencial entre A e B e a mesma impedância do circuito original.
Este teorema foi dado a conhecer em 1883 pelo engenheiro francês Léon Charles Thévenin, mas afirma-se que foi enunciado trinta anos antes pelo físico alemão Hermann von Helmholtz.

Sua utilidade reside no fato de que, mesmo quando o circuito original é complexo ou desconhecido, para efeitos de uma carga ou impedância que é colocada entre os terminais A e B, o circuito equivalente Thévenin simples se comporta da mesma maneira que o original.
Índice do artigo
- 1 Como você calcula a tensão equivalente passo a passo?
- 1.1 - Experimentalmente
- 1.2 - Resolvendo o circuito
- 2 Aplicações do teorema de Thévenin (parte I)
- 2.1 Exemplo 1a (cálculo da tensão equivalente passo a passo)
- 2.2 Exemplo 1b (corrente na carga usando o equivalente Thévenin)
- 3 Prova do teorema de Thévenin
- 4 Aplicação do teorema de Thévenin (parte II)
- 4.1 Exemplo 2a (resistência equivalente a Thévenin)
- 4.2 Exemplo 2b
- 4.3 Exemplo 2c
- 5 Aplicação do teorema de Thévenin (parte III)
- 5.1 Exemplo 3
- 6 referências
Como você calcula a tensão equivalente passo a passo?
A tensão ou diferença de potencial do circuito equivalente pode ser obtida das seguintes maneiras:
- Experimentalmente
Obtendo a tensão Thévenin equivalente
Se for um dispositivo ou equipamento que está em uma “caixa preta”, a diferença de potencial entre os terminais A e B é medida com um voltímetro ou osciloscópio. É muito importante que nenhuma carga ou impedância seja colocada entre os terminais A e B.
Um voltímetro ou osciloscópio não representa nenhuma carga nos terminais, pois ambos os dispositivos têm uma impedância muito grande (idealmente infinita) e seria como se os terminais A e B estivessem sem carga. A voltagem ou voltagem obtida desta forma é a voltagem equivalente Thévenin.
Obtendo a impedância equivalente Thévenin
Para obter a impedância equivalente de uma medição experimental, uma resistência conhecida é colocada entre os terminais A e B e a queda de tensão ou sinal de tensão é medida com um osciloscópio..
A partir da queda de tensão na resistência conhecida entre os terminais, a corrente que flui através dele pode ser obtida.
O produto da corrente obtida com a resistência equivalente mais a queda de tensão medida na resistência conhecida é igual à tensão Thévenin equivalente obtida anteriormente. Desta igualdade, a impedância Thévenin equivalente é liberada.
- Resolvendo o circuito
Cálculo da tensão equivalente Thévenin
Primeiro, qualquer carga ou impedância é desconectada dos terminais A e B.
Como o circuito é conhecido, a teoria da malha ou as leis de Kirchhoff são aplicadas para encontrar a tensão nos terminais. Essa tensão será o equivalente a Thévenin.
Cálculo da impedância equivalente Thévenin
Para obter a impedância equivalente, procedemos a:
- Substitua as fontes de tensão do circuito original por curtos-circuitos de "impedância zero" e as fontes de corrente do circuito original por abertas de "impedância infinita".
- Em seguida, a impedância equivalente é calculada seguindo as regras de impedâncias em série e impedâncias paralelas.
Aplicações do teorema de Thévenin (parte I)
Aplicaremos o teorema de Thévenin para resolver alguns circuitos. Nesta primeira parte consideramos um circuito que possui apenas fontes de tensão e resistências.
Exemplo 1a (cálculo de tensão equivalente passo a passo)
A Figura 2 mostra o circuito que está em uma caixa celestial que tem duas baterias de força eletromotriz V1 e V2 respectivamente e resistores R1 e R2, o circuito tem terminais A e B nos quais uma carga pode ser conectada.
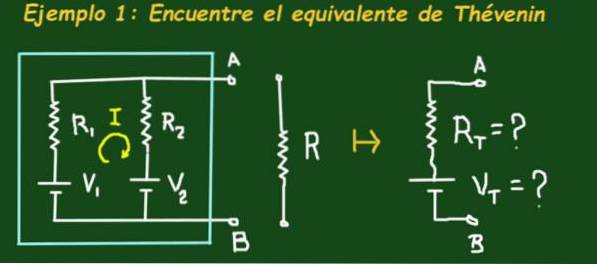
O objetivo é encontrar o circuito equivalente de Thévenin, ou seja, determinar os valores de Vt e Rt do circuito equivalente. Aplique os seguintes valores: V1 = 4V, V2 = 1V, R1 = 3Ω, R2 = 6Ω e R = 1Ω.
Solução passo a passo
Passo 1
Determinaremos a tensão nos terminais A e B quando nenhuma carga for colocada neles.
Passo 2
O circuito a ser resolvido consiste em uma única malha pela qual circula uma corrente I que tomamos positiva no sentido horário..
etapa 3
Percorremos a malha começando com o canto esquerdo inferior. O caminho leva à seguinte equação:
V1 - I * R1 - I * R2 - V2 = 0
Passo 4
Resolvemos para a corrente de malha I e obtemos:
I = (V1 -V2) / (R1 + R2) = (4V - 1V) / (3Ω + 6Ω) = ⅓ A
Etapa 5
Com a corrente de malha, podemos determinar a diferença de tensão entre A e B, que é:
Vab = V1 - I * R1 = 4V - ⅓ A * 3Ω = 3V
Ou seja, a tensão equivalente de Thévenin é: Vt = 3V.
Etapa 6 (resistência equivalente a Thévenin)
Passamos agora a calcular a resistência equivalente de Thévenin, para a qual e como mencionado anteriormente, as fontes de tensão são substituídas por um cabo.
Nesse caso, temos apenas dois resistores em paralelo, então a resistência equivalente Thévenin é:
Rt = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω
Exemplo 1b (corrente na carga usando o equivalente Thévenin)
Conecte como uma carga aos terminais A e B uma resistência R = 1Ω ao circuito equivalente e encontre a corrente que flui através da referida carga.
Solução
Quando a resistência R é conectada ao circuito equivalente de Thévenin, temos um circuito simples que consiste em uma fonte Vt uma resistência Rt em série com a resistência R.
Chamaremos Ic a corrente que flui através da carga R, de modo que a equação da malha se pareça com esta:
Vt - Ic * Rt - Ic * R = 0
a partir do qual se segue que Ic é dado por:
Ic = Vt / (Rt + R) = 3V / (2Ω + 1Ω) = 1 A
Prova do teorema de Thévenin
Para verificar se o teorema de Thévenin é válido, conecte R ao circuito original e encontre a corrente fluindo através de R aplicando a lei da malha ao circuito resultante.
O circuito resultante permanece e suas equações de malha permanecem como mostrado na figura a seguir:
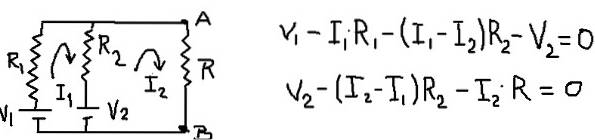
Ao adicionar as equações da malha, é possível encontrar a corrente da malha I1 como uma função da corrente I2. Em seguida, ele é substituído na segunda equação da malha e uma equação é deixada com I2 como a única incógnita. A tabela a seguir mostra as operações.
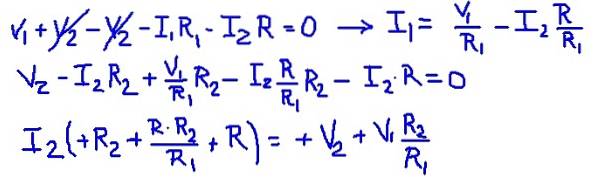
Em seguida, os valores das resistências e tensões das fontes são substituídos, obtendo-se o valor numérico da corrente de malha I2.

A corrente da malha I2 é a corrente que flui através da resistência de carga R e o valor encontrado de 1 A coincide totalmente com o encontrado anteriormente com o circuito Thévenin equivalente..
Aplicação do teorema de Thévenin (parte II)
Nesta segunda parte, o teorema de Thévenin será aplicado em um circuito que possui fontes de tensão, fonte de corrente e resistências..
Exemplo 2a (resistência equivalente a Thévenin)
O objetivo é determinar o circuito equivalente de Thévenin correspondente ao circuito da figura a seguir, quando os terminais estão sem a resistência de 1 ohm, então a resistência é colocada e a corrente que circula por ela é determinada.
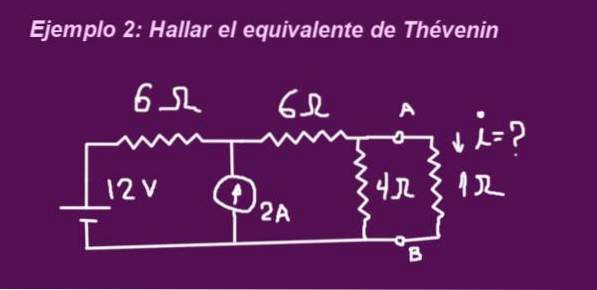
Solução
Para encontrar a resistência equivalente, remova a resistência de carga (neste caso, 1 ohm). Além disso, as fontes de tensão são substituídas por um curto-circuito e as fontes de corrente por um circuito aberto..
Desta forma, o circuito para o qual a resistência equivalente será calculada é o mostrado abaixo:
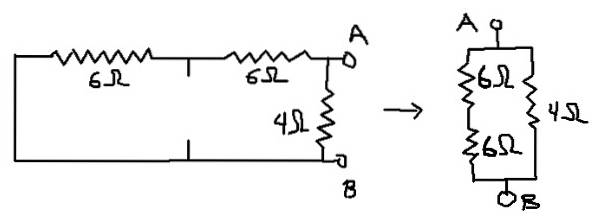
Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω que é a resistência equivalente de Thévenin (Rth).
Exemplo 2b
Calcule a tensão equivalente Thévenin.
Solução
Para calcular a tensão equivalente de Thévenin consideramos o seguinte circuito, no qual colocaremos as correntes em I1 e I2 nos ramos indicados na figura a seguir:
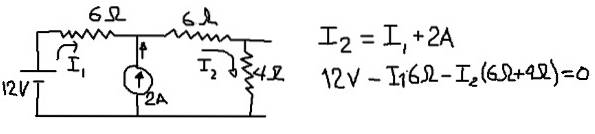
A figura anterior mostra a equação dos nós de corrente e a equação das tensões quando a malha externa é atravessada. A partir da segunda das equações, o I1 atual é limpo:
I1 = 2 - I2 * (5/3)
Esta equação é substituída na equação dos nós:
I2 = 2 - (5/3) I2 + 2 ===> I2 (8/3) = 4 ===> I2 = 12/8 = 1,5 A
Isso significa que a queda de tensão no resistor de 4 ohms é de 6 volts..
Em suma, a tensão Thévenin é Vth = 6 V.
Exemplo 2c
Encontrando o Circuito Equivalente de Thevenin e a Corrente no Resistor de Carga.
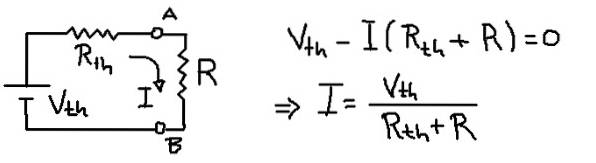
Solução
A figura anterior mostra o circuito equivalente de Thévenin com a resistência de carga R. A partir da equação de tensão na malha, a corrente I que flui através da resistência de carga R é deduzida.
I = Vth / (Rth + R) = 6V / (3Ω + 1Ω) = 1,5 A
Aplicação do teorema de Thévenin (parte III)
Nesta terceira parte da aplicação do teorema de Thévenin, é considerado um circuito de corrente alternada que contém uma fonte de tensão alternada, um capacitor, uma indutância e uma resistência..
Exemplo 3
O objetivo é encontrar o Circuito Thévenin equivalente ao seguinte circuito:
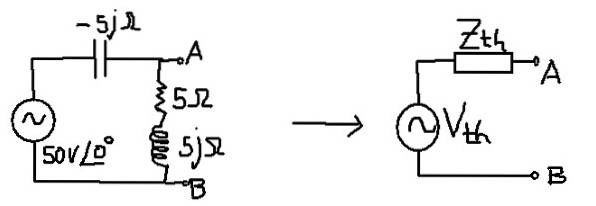
Solução
A impedância equivalente corresponde à do capacitor em paralelo com a combinação em série da resistência e indutância.
O inverso da impedância equivalente é dado por:
Zeq ^ -1 = (-5j) ^ - 1 + (5 + 5j) ^ - 1 = (1/5) j + ((1/10 + (1/10) j) = (1/10 + 3 / 10 j) Mho
E a impedância equivalente será então:
Zeq = (1 - 3 j) Ohm
A corrente complexa I pode ser derivada da equação da malha:
50V∠0 - I (-5 j + 5 + 5j) = 50V∠0 - I * 5 = 0 ===> I = 10A ∠0
Calcula-se agora a queda de tensão na resistência mais a indutância, ou seja, a tensão Vab que será a tensão Thévenin equivalente:
Vab = I * (5 + 5 j) Ω = 10A ∠0 * 5Ω∠45º = 50V∠45º
Em outras palavras, a tensão equivalente tem o mesmo valor de pico da fonte original, mas está 45 graus fora de fase: Vth = 50V∠45º
Referências
- Tutoriais de eletrônica, teorema de Thevenin. Recuperado de: electronics-tutorials.ws
- Perguntas e respostas sobre a teoria das redes. Teorema de Thevenin. Recuperado de: sanfoundry.com
- Teorema de Thevenin. Procedimento passo a passo. Recuperado de: electricaltechnology.org
- Teorema de Thevenin. Resolvido exemplo passo a passo. Recuperado de: electricalsimple.blogspot.com
- Workshop sobre os teoremas de Thevenin e Norton. Recuperado de: web.iit.edu
- Wikipedia. Teorema de Thévenin. Recuperado de: wikipedia.com



Ainda sem comentários