
Teorema do fator de explicação, exemplos, exercícios
O teorema do fator afirma que um polinômio P (x) é divisível por um binômio da forma (x - a) se x = a é uma raiz de P (x), ou seja, P (a) = 0. Diz-se que um polinômio é divisível entre outro quando seu residual ou resto é zero.
Um polinômio é uma expressão da forma:
P (x) = an xn + paran-1 xn-1 +… + A1 x + a0

Onde:
-n é o grau do polinômio, onde n é o maior inteiro ao qual a variável independente x é elevada,
-Os valores paran, paran-1 ,… + A1 , para0 são os coeficientes do polinômio, que geralmente são números reais, mas também podem ser números complexos.
Um polinômio de grau n pode ser decomposto como o produto de n binômios da forma:
(x - reu)
Onde estáeu é a i-ésima raiz de P (x):
P (x) = an (x - r1) (x - rdois)… (X - rn)
Como o número de raízes de um polinômio é igual ao seu grau.
Índice do artigo
- 1 exemplos
- 1.1 - Exemplo 1
- 1.2 - Exemplo 2
- 2 exercícios
- 2.1 - Exercício 1
- 2.2 - Exercício 2
- 3 referências
Exemplos
- Exemplo 1
Vamos considerar por caso o polinômio:
P (x) = 3⋅xdois - 7⋅x + 2
Você quer saber se este polinômio é divisível pelo binômio (x - 2). Se o teorema do fator for usado, devemos avaliar P (x = 2) para saber se o valor 2 é uma raiz ou não. Em seguida, procedemos para avaliar a expressão:
P (2) = 3⋅22 - 7⋅2 + 2 = 3⋅4 - 7⋅2 + 2 = 12 - 14 + 2 = 12 - 12 = 0.
Acontece que x = 2 é a raiz de P (x), então de acordo com o teorema do fator, o binômio (x - 2) é efetivamente um fator de P (x).
Vamos prosseguir para a verificação direta por divisão. O detalhe de como a divisão é realizada é mostrado na figura a seguir:
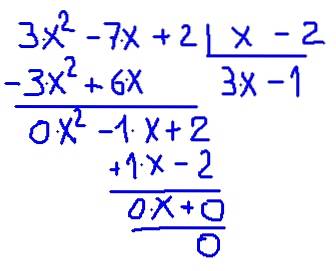
Verifica-se que o quociente entre P (x) e (x-2) dá um polinômio de menor grau denominado quociente C (x) = 3⋅x - 1 com resto 0.
Podemos resumir o resultado da seguinte forma:
(3⋅xdois - 7⋅x + 2) ÷ (x -2) = (3⋅x - 1) + 0
A expressão anterior pode ser escrita de outra forma, simplesmente lembrando que o dividendo P (x) é igual ao produto do divisor (x -2) pelo quociente (3⋅x - 1) mais o resto (zero neste caso ):
(3⋅xdois - 7⋅x + 2) = (x -2) (3⋅x - 1) + 0
Dessa forma foi possível fatorar o polinômio P (x), ou seja, escrever como produto de polinômios, o polinômio original:
(3⋅xdois - 7⋅x + 2) = (x -2) (3⋅x - 1)
- Exemplo 2
Seja o polinômio Q (x) = x3 - x + 2. Queremos saber se é divisível pelo binômio (x + 1).
A maneira mais direta é simplesmente aplicar o teorema do fator. Neste caso, simplesmente temos que verificar se x = -1 cancela ou não o polinômio Q (x).
Prosseguimos substituindo:
Q (-1) = (-1)3 - (-1) + 2 = -1 + 1 + 2 = 2
O resultado é diferente de zero, pois o teorema do fator nos garante que o polinômio Q (x) não é divisível por (x + 1), pois Q (-1) ≠ 0.
Agora procederemos a realizar a divisão de Q (x) pelo binômio (x + 1) como método de verificação de nossa conclusão.
Nesta ocasião, a divisão será realizada pelo método da divisão sintética, que consiste em colocar na primeira linha ordenada do grau mais alto ao grau zero todos os coeficientes do polinômio, inclusive os faltantes, por possuírem coeficiente zero..
Então, na primeira coluna, o termo independente do divisor é colocado, mas com o sinal alterado, no nosso caso o divisor é (x + 1). Seu termo independente é 1, mas como na primeira coluna é colocado o sinal alterado, ou seja, -1.
A figura a seguir ilustra como a divisão sintética é feita:

Com este resultado verifica-se que (x + 1) não é um fator do polinômio Q (x) = x3 - x + 2 visto que o resto não é zero.
Esta conclusão não é surpreendente, pois já havia sido prevista com o teorema do fator. Observe também que ao substituir x = -1 em Q (x) o que é obtido é precisamente o resto ou resto da divisão dos polinômios, uma vez que Q (-1) = resto = 2.
Claro, a divisão fornece as informações adicionais do quociente C (x) = xdois - x.
Lembrando que o dividendo Q (x) é igual ao divisor (x + 1) pelo quociente C (x) mais o resto r = 2, temos a expansão do polinômio Q (x) da seguinte forma:
Q (x) = (x + 1) (xdois - x) + 2 = x (x + 1) (x - 1) + 2
Deve-se notar que esta expressão não é a fatoração do referido polinômio, uma vez que existe uma soma de termo diferente de zero, que é justamente o resto do valor 2.
Treinamento
- Exercício 1
Encontre os fatores do polinômio
P (x) = x3 - 5 xdois + 2 x + 8
E também escreva sua fatoração.
Solução
O teorema do fator nos diz que devemos procurar as raízes para para então encontrar os fatores (x - para), neste caso como é um polinômio de grau três, deve haver três raízes.
Por se tratar de um polinômio com coeficientes inteiros, as raízes devem estar entre os divisores do termo independente, que neste caso é 8. Esses divisores são:
± 1, ± 2, ± 4, ± 8.
Começamos explorando +1: P (+1) = 13 - 5⋅ 1dois + 2⋅1 + 8 = 1 - 5 + 2 + 8 = 6 que é diferente de 0, portanto, +1 não é uma raiz.
Exploramos -1:
P (-1) = (-1)3 - 5⋅ (-1)dois + 2⋅ (-1) + 8 = -1 - 5 - 2 + 8 = 0
Do resultado conclui-se que -1 é a raiz de P (x) e (x - (-1)) = (x + 1) é um fator do polinômio.
Mais dois fatores ainda precisam ser encontrados:
Provamos o seguinte, que é +2:
P (+2) = (+2)3 - 5⋅ (+2)dois + 2⋅ (+2) + 8 = 8 + (-20) + 4 + 8 = 0
Novamente obtemos zero. Portanto, o outro fator é (x - 2).
Como é um polinômio de grau três, precisamos apenas encontrar um fator. Agora testamos o valor +4 para descobrir se ele cancela o polinômio:
P (+4) = (+4)3 - 5⋅ (+4)dois + 2⋅ (+4) + 8 = 64 - 80 + 8 + 8 = 0.
Ou seja, +4 é a raiz de P (x) e, portanto, o binômio (x - 4) é outro de seus fatores.
Chega de pesquisar, pois é um polinômio de grau 3 que possui no máximo três raízes. Neste exercício, todas as raízes tornaram-se reais e inteiras.
Portanto, o polinômio P (x) é fatorado assim:
P (x) = x3 - 5 xdois + 2 x + 8 = (x + 1) (x - 2) (x - 4).
- Exercício 2
Seja o polinômio p⋅x3 - x + 2p. Determine o valor de p de modo que o polinômio seja divisível por (x + 2).
Solução
Usamos o teorema do fator, que afirma que se x = -2 cancela o polinômio, então (x - (-2)) é um fator do referido polinômio.
Em seguida, substituímos x por (-2) no polinômio original, simplificamos e definimos igual a zero:
p⋅ (-2)3 - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0
Agora, o valor de p é limpo para que a igualdade com zero seja satisfeita:
p = -2 / 10 = -⅕
Isso significa que o polinômio:
-⅕⋅x3 - x - ⅖
É divisível por (x + 2), ou o que é equivalente: (x + 2) é um de seus fatores.
Referências
- Baldor Aurelio. Álgebra. Grupo Editorial Patria.
- Demana, W. Precalculus: Graphical, Numerical, Algebraic 7th Ed. Pearson Education.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- Stewart, J. 2006. Pré-cálculo: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
- Zill, D. 1984. Algebra and Trigonometry. Colina Mcgraw.


Ainda sem comentários