Características de tiro parabólico, fórmulas e equações, exemplos

O tiro parabólico Consiste em lançar um objeto ou projétil em determinado ângulo e deixá-lo mover-se sob a ação da gravidade. Se a resistência do ar não for considerada, o objeto, independentemente de sua natureza, seguirá um caminho de arco de parábola.

É um movimento diário, pois entre os esportes mais populares estão aqueles em que as bolas ou bolas são lançadas, seja com a mão, com o pé ou com um instrumento como uma raquete ou um taco por exemplo..

Para seu estudo, o plano parabólico é dividido em dois movimentos sobrepostos: um horizontal sem aceleração e outro vertical com aceleração constante para baixo, que é a gravidade. Ambos os movimentos têm velocidade inicial.

Digamos que o movimento horizontal seja executado ao longo do eixo xe o movimento vertical ao longo do eixo y. Cada um desses movimentos é independente um do outro.

Uma vez que determinar a posição do projétil é o objetivo principal, é necessário escolher um sistema de referência apropriado. Os detalhes estão abaixo.

Índice do artigo

• 1 Fórmulas e equações de tiro parabólico
  • 1.1 - Trajetória, altura máxima, tempo máximo e alcance horizontal
• 2 exemplos de tiro parabólico
  • 2.1 Tiro parabólico em atividades humanas
  • 2.2 O tiro parabólico na natureza
• 3 exercício
• 4 referências

Fórmulas e equações de tiro parabólico

Suponha que o objeto seja lançado com ângulo α em relação à velocidade horizontal e inicial v_ou conforme mostrado na figura abaixo à esquerda. O tiro parabólico é um movimento que ocorre no avião xy e, nesse caso, a velocidade inicial é quebrada assim:

v_boi = v_ou cos α

v_Ei = v_ou sin α

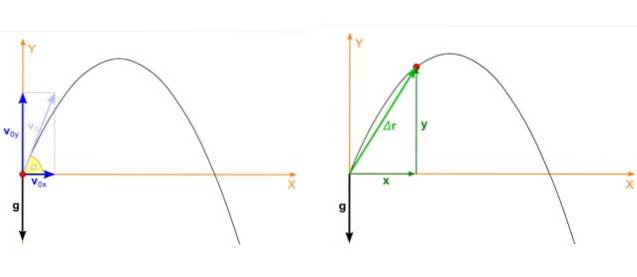
A posição do projétil, que é o ponto vermelho na figura 2, imagem à direita, também tem dois componentes dependentes do tempo, um em x e o outro em Y. A posição é um vetor denotado como r e suas unidades são de comprimento.

Na figura, a posição inicial do projétil coincide com a origem do sistema de coordenadas, portanto x_ou = 0, e_ou = 0. Nem sempre é o caso, você pode escolher a origem em qualquer lugar, mas esta escolha simplifica muito os cálculos.

Quanto aos dois movimentos em x e em y, são:

-x (t): é um movimento retilíneo uniforme.

-y (t): corresponde a um movimento retilíneo uniformemente acelerado com g = 9,8 m / s^dois e apontando verticalmente para baixo.

Na forma matemática:

x (t) = v_ou cos α.t

y (t) = v_ou .sin α.t - ½g.t^dois

O vetor de posição é:

r (t) = [v_ou cos α.t]eu + [v_ou .sin α.t - ½g.t^dois] j

Nessas equações, o leitor atento perceberá que o sinal negativo é devido à gravidade apontando para o solo, a direção escolhida como negativa, enquanto para cima é considerada positiva..

Uma vez que a velocidade é a primeira derivada da posição, simplesmente derivar r (t) com relação ao tempo e obter:

v (t) = v_ou cos α eu + (v_ou .sin α - gt) j

Finalmente, a aceleração é expressa vetorialmente como:

para (t) = -g j

- Trajetória, altura máxima, tempo máximo e alcance horizontal

Trajetória

Para encontrar a equação explícita do caminho, que é a curva y (x), devemos eliminar o parâmetro tempo, resolvendo na equação por x (t) e substituindo por y (t). A simplificação é um tanto trabalhosa, mas finalmente você obtém:

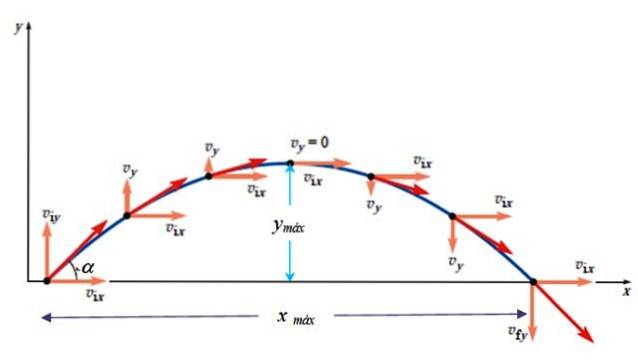
Altura máxima

A altura máxima ocorre quando v_Y = 0. Sabendo que existe a seguinte relação entre a posição e o quadrado da velocidade:

v_Y^dois = v_Ei ^dois- 2gy

Fazendo v_Y = 0 apenas ao atingir a altura máxima:

0 = v_Ei ^dois- 2g. E_max → e_max = v_Ei ^dois/ 2 g

Com:

v_Ei = v_ou senα

Tempo máximo

O tempo máximo é o tempo que leva para o objeto alcançar e_max. Para calculá-lo é usado:

v_Y = v_ou .sin α - gt

Sabendo que v_Y torna-se 0 quando t = t_max, resultado:

v_ou .sin α - g.t_max = 0

t_max = v_Ei / g

Alcance horizontal máximo e tempo de vôo

O alcance é muito importante, pois sinaliza onde o objeto cairá. Assim saberemos se atinge ou não o alvo. Para encontrá-lo, precisamos do tempo de voo, tempo total ou t_v.

A partir da ilustração acima, é fácil concluir que t_v = 2.t_max. Mas cuidado, isso só é verdade se o lançamento estiver nivelado, ou seja, a altura do ponto de partida for igual à altura da chegada. Caso contrário, o tempo é encontrado resolvendo a equação quadrática que resulta da substituição da posição final Y_final:

Y_final = v_ou .sin α.t_v - ½g.t_v^dois

Em qualquer caso, o alcance horizontal máximo é:

x_max = v_boi. t_v

Exemplos de tiro parabólico

O disparo parabólico faz parte do movimento de pessoas e animais. Também de quase todos os esportes e jogos onde a gravidade intervém. Por exemplo:

Tiro parabólico em atividades humanas

-A pedra atirada por uma catapulta.

-O chute de gol do goleiro.

-A bola lançada pelo arremessador.

-A flecha que sai do arco.

-Todos os tipos de saltos

-Jogue uma pedra com uma funda.

-Qualquer arma de arremesso.

O tiro parabólico na natureza

-Água que jorra de jatos naturais ou artificiais, como os de uma fonte.

-Pedras e lava jorrando de um vulcão.

-Uma bola que quica no pavimento ou uma pedra que quica na água.

-Todos os tipos de animais saltadores: cangurus, golfinhos, gazelas, gatos, sapos, coelhos ou insetos, para citar alguns.

Exercício

Um gafanhoto salta em um ângulo de 55º com a horizontal e cai 0,80 metros à frente. Achar:

a) A altura máxima atingida.

b) Se ele saltasse com a mesma velocidade inicial, mas formando um ângulo de 45º, ele iria mais alto??

c) O que pode ser dito sobre o alcance horizontal máximo para este ângulo?

Solução para

Quando os dados fornecidos pelo problema não contêm a velocidade inicial v_ou os cálculos são um pouco mais trabalhosos, mas a partir das equações conhecidas, uma nova expressão pode ser derivada. Partindo de:

x_max = v_boi . t_voar = v_ou.cos α. t_v

Quando ele pousa mais tarde, a altura retorna a 0, então:

v_ou .sin α.t_v - ½g.t_v^dois= 0

o que t_v é um fator comum, é simplificado:

v_ou .sin α - ½g.t_v= 0

Podemos limpar t_v da primeira equação:

t_v = x_max / v_ou.cos α

E substitua no segundo:

v_ou .sin α - (½g.x_max / v_ou.cos α) = 0

Multiplicando todos os termos por v_ou.cos αa expressão não é alterada e o denominador desaparece:

(v_ou .sin α.) (v_ou.cos α) - ½g.x_max = 0

v_ou^dois sin α. cos α = ½g.x_max

Já pode ser apagado v_ou ou também substituir a seguinte identidade:

sin 2α = 2 sin α. cos α → v_ou^dois sin 2α = g.x_max

Calcula-se v_ou^dois:

v_ou^dois = g.x_max / sen 2α = (9,8 x 0,8 / sen 110) m^dois/ s^dois = 8,34 m^dois/ s^dois

E finalmente a altura máxima:

Y_max= v_Ei ^dois/ 2g = (8,34 x pecado^dois 55) / (2 x 9,8) m = 0,286 m = 28,6 cm

Solução b

A lagosta consegue manter a mesma velocidade horizontal, mas diminuindo o ângulo:

Y_max= v_Ei ^dois/ 2g = (8,34 x pecado^dois 45) / (2 x 9,8) m = 0,213 m = 21,3 cm

Alcança uma altura menor.

Solução c

O alcance horizontal máximo é:

x_max = v_ou^dois sen 2o / g

Ao variar o ângulo, o alcance horizontal também muda:

x_max = 8,34 sen 90 / 9,8  m = 0,851 m = 85,1 cm

O salto é mais longo agora. O leitor pode verificar que é máximo para o ângulo de 45º porque:

sin 2α = sin 90 = 1.

Referências

1. Figueroa, D. 2005. Série: Física para Ciências e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).
2. Giambattista, A. 2010. Física. Segunda edição. Colina Mcgraw.
3. Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed Prentice Hall.
4. Resnick, R. 1999. Physics. Vol. 1. 3ª Ed. Em espanhol. Compañía Editorial Continental S.A. por C.V.
5. Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 1.