
Características de tiro parabólico oblíquo, fórmulas, equações, exemplos
O tiro parabólico oblíquo é um caso particular de movimento de queda livre em que a velocidade inicial do projétil forma um certo ângulo com a horizontal, resultando em uma trajetória parabólica.
Queda livre é um caso de movimento com aceleração constante, em que a aceleração é a da gravidade, que sempre aponta verticalmente para baixo e tem magnitude de 9,8 m / s ^ 2. Não depende da massa do projétil, como Galileo Galilei mostrou em 1604.
Se a velocidade inicial do projétil é vertical, a queda livre tem uma trajetória reta e vertical, mas se a velocidade inicial é oblíqua então a trajetória de queda livre é uma curva parabólica, fato também demonstrado por Galileu.
Exemplos de movimento parabólico são a trajetória de uma bola de beisebol, a bala disparada de um canhão e o jato de água saindo de uma mangueira..
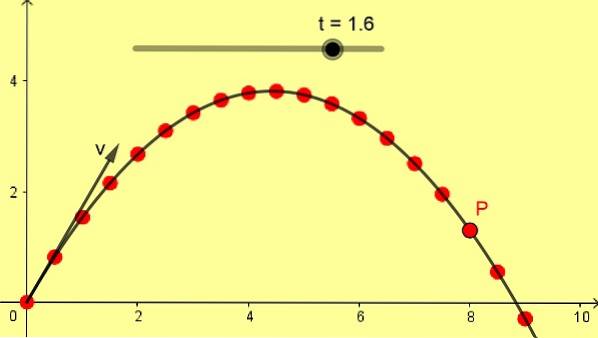
A Figura 1 mostra um calado parabólico oblíquo de 10 m / s com ângulo de 60º. A escala está em metros e as posições sucessivas de P são tomadas com uma diferença de 0,1 s a partir do instante inicial 0 segundos.
Índice do artigo
- 1 Fórmulas
- 1.1 Posição e velocidade
- 2 equações
- 2.1 Equações paramétricas
- 2.2 Equação da trajetória
- 3 exemplos
- 3.1 Exemplo 1
- 3.2 Exemplo 2
- 3.3 Exemplo 3
- 4 referências
Fórmulas
O movimento de uma partícula é totalmente descrito se sua posição, velocidade e aceleração forem conhecidas em função do tempo..
O movimento parabólico resultante de um tiro oblíquo é a superposição de um movimento horizontal em velocidade constante, mais um movimento vertical com aceleração constante igual à aceleração da gravidade..
As fórmulas que se aplicam ao calado parabólico oblíquo são aquelas que correspondem a um movimento com aceleração constante a = g, note que negrito foi usado para indicar que a aceleração é uma quantidade vetorial.
Posição e velocidade
Em um movimento com aceleração constante, a posição depende matematicamente do tempo na forma quadrática.
Se denotarmos r(t) posição na hora t, rou a posição no instante inicial, vou velocidade inicial, g aceleração e t = 0 como o instante inicial a fórmula que dá a posição para cada instante de tempo t isso é:
r(t) = rou + vou t + ½ g tdois
O negrito na expressão acima indica que é uma equação vetorial.
A velocidade em função do tempo é obtida tomando a derivada em relação a t da posição e o resultado é:
v(t) = vou + g t
E para obter a aceleração em função do tempo, a derivada da velocidade em relação a t resultando:
para(t) = g
Quando o tempo não está disponível, há uma relação entre velocidade e posição, que é dada por:
vdois = voudois - 2 g (e - eu)
Equações
A seguir, encontraremos as equações que se aplicam a um tiro parabólico oblíquo na forma cartesiana.
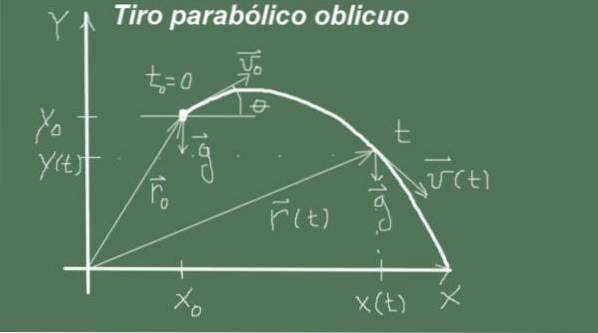
O movimento começa no instante t = 0 com posição inicial (xo, eu) e velocidade de magnitude vou e ângulo θ, ou seja, o vetor de velocidade inicial é (vou cosθ, vou senθ). O movimento prossegue com aceleração
g = (0, -g).
Equações paramétricas
Se a fórmula vetorial que dá a posição em função do tempo for aplicada e os componentes forem agrupados e equalizados, então as equações que dão as coordenadas da posição em qualquer instante do tempo t serão obtidas.
x (t) = xou + vboi t
y (t) = you + vEi t -½ g tdois
Da mesma forma, temos as equações para os componentes da velocidade em função do tempo.
vx(t) = vboi
vY(t) = vEi - g t
Onde: vboi = vou cosθ; vEi = vou senθ
Equação da trajetória
y = A x ^ 2 + B x + C
A = -g / (2 vboi^ 2)
B = (vEi/ vboi + g xou/ vboi^ 2)
C = (eou - vEi xou / vboi)
Exemplos
Exemplo 1
Responda as seguintes questões:
a) Por que nos problemas de tiragem parabólica o efeito do atrito com o ar geralmente é negligenciado??
b) A forma do objeto tem alguma importância no plano parabólico?
Respostas
a) Para que o movimento de um projétil seja parabólico, é importante que a força de atrito do ar seja muito menor que o peso do objeto sendo lançado.
Se uma bola de cortiça ou algum material leve é lançado, a força de atrito é comparável ao peso e sua trajetória não pode se aproximar de uma parábola.
Pelo contrário, se for um objeto pesado, como uma pedra, a força de atrito é insignificante em comparação com o peso da pedra e sua trajetória se aproxima de uma parábola.
b) A forma do objeto arremessado também é relevante. Se uma folha de papel for lançada com a forma de um avião, seu movimento não será em queda livre ou parabólica, pois o formato favorece a resistência do ar.
Por outro lado, se a mesma folha de papel for compactada em uma bola, o movimento resultante é muito semelhante a uma parábola.
Exemplo 2
Um projétil é lançado do solo horizontal com velocidade de 10 m / se ângulo de 60º. Esses são os mesmos dados com os quais foi elaborada a Figura 1. Com esses dados, encontre:
a) Momento em que atinge a altura máxima.
b) A altura máxima.
c) Velocidade na altura máxima.
d) Posição e velocidade em 1,6 s.
e) No momento em que atinge o solo novamente.
f) O alcance horizontal.
Solução para)
A velocidade vertical em função do tempo é
vY(t) = vEi - g t = vou sinθ - g t = 10 sin60º - 9,8 t = 8,66 - 9,8 t
No momento em que a altura máxima é atingida, a velocidade vertical é zero por um instante.
8,66 - 9,8 t = 0 ⇒ t = 0,88 s.
Solução b)
A altura máxima é dada pela coordenada Y para o instante em que essa altura é atingida:
e (0,88s) = I + go t -½ g t ^dois = 0 + 8,66 * 0,88-½ 9,8 0,88 ^dois =
3,83 m
Portanto, a altura máxima é 3,83 m.
Solução c)
A velocidade na altura máxima é horizontal:
vx(t) = vboi = vou cosθ = 10 cos60º = 5 m / s
Solução d)
A posição em 1,6 s é:
x (1,6) = 5 * 1,6 = 8,0 m
e (1,6) = 8,66 * 1,6-½ 9,8 1,6dois = 1,31 m
Solução e)
Quando a coordenada y toca o solo, então:
y (t) = 8,66 * t-½ 9,8 tdois = 0 ⇒ t = 1,77 s
Solução f)
O alcance horizontal é a coordenada x no momento em que toca o solo:
x (1,77) = 5 * 1,77 = 8,85 m
Exemplo 3
Encontre a equação da trajetória com os dados do Exemplo 2.
Solução
A equação paramétrica do caminho é:
x (t) = 5 * t
y (t) = 8,66 * t-½ 9,8 t ^dois
E a equação cartesiana é obtida resolvendo t do primeiro e substituindo no segundo
y = 8,66 * (x / 5) -½ 9,8 (x / 5) ^dois
Simplificando:
y = 1,73 x - 0,20 x ^ 2
Referências
- P. P. Teodorescu (2007). "Cinemática". Sistemas Mecânicos, Modelos Clássicos: Mecânica de Partículas. Springer.
- Resnick, Halliday & Krane (2002). Física Volume 1. Cecsa, México.
- Thomas Wallace Wright (1896). Elementos de mecânica, incluindo cinemática, cinética e estática. E e FN Spon.
- Wikipedia. Movimento parabólico. Recuperado de es.wikipedia.org.
- Wikipedia. Movimento do projétil recuperado de en.wikipedia.org.


Ainda sem comentários