Fórmulas de tiro vertical, equações, exemplos

O tiro vertical É um movimento que ocorre sob a ação de um campo de força, comumente o da gravidade, e pode ser ascendente ou descendente. Também é conhecido pelo nome de lançamento vertical.

O exemplo mais imediato é jogar para cima (ou para baixo, se preferir) uma bola com a mão, é claro, certificando-se de fazer isso na direção vertical. Desconsiderando a resistência do ar, o movimento que a bola segue se encaixa perfeitamente no modelo Uniformly Varied Rectilinear Motion (MRUV)..

O tiro vertical é um movimento amplamente estudado nos cursos de introdução à física, pois é uma amostra do movimento em uma dimensão, um modelo muito simples e útil.

Este modelo não só pode ser usado para estudar a cinemática de objetos sob a ação da gravidade, mas também, como será visto mais tarde, descreve o movimento de partículas em meio a um campo elétrico uniforme..

Índice do artigo

• 1 Fórmulas e equações
  • 1.1 Equações de lançamento vertical
• 2 exemplos
  • 2.1 Exemplo trabalhado 1
  • 2.2 Exemplo trabalhado 2
• 3 referências

Fórmulas e equações

A primeira coisa que se precisa é um sistema de coordenadas para indicar a origem e etiquetá-la com uma letra, que no caso de movimentos verticais é a letra "Y".

Então a direção positiva é selecionada +Y, que geralmente é para cima e o sentido -Y que geralmente é retirado (veja a figura 2). Tudo isso, a menos que o solucionador de problemas decida de outra forma, já que outra opção é considerar a direção do movimento como positiva, seja ela qual for..

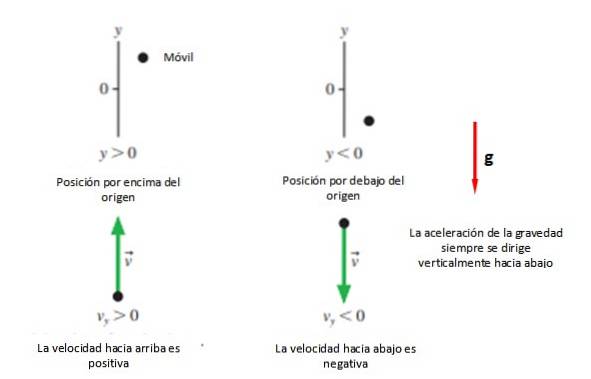
Em qualquer caso, é recomendado que a origem coincida com o ponto de lançamento. Y_ou, porque desta forma as equações são simplificadas, embora você possa tomar qualquer posição que quiser para começar a estudar o movimento.

Equações de lançamento vertical

Depois de estabelecer o sistema de coordenadas e a origem, vamos para as equações. As magnitudes que descrevem o movimento são:

-Velocidade inicial v_ou

-Aceleração para

-Velocidade v

-Posição inicial x_ou

-Posição x

-Deslocamento Dx

-Clima t

Todos, exceto o tempo, são vetores, mas como é um movimento unidimensional com uma determinada direção, o que importa é usar os sinais + ou - para indicar para onde está indo a magnitude em questão. No caso de calado vertical, a gravidade sempre desce e, salvo indicação em contrário, é atribuído um sinal -.

A seguir estão as equações adaptadas para inclinação vertical, substituindo “x" para "Y"Y"para" para "g”. Além disso, o sinal (-) correspondente à gravidade direcionado para baixo será incluído imediatamente:

1) Posição: y = y_ou + v_ou.t - ½ g.t^dois

2) Velocidade: v = v_ou - g.t

3) Velocidade em função do deslocamento ΔY: v^dois = v_ou^dois - 2 g. ΔY

Exemplos

Abaixo estão exemplos de aplicação para tiro vertical. Em sua deliberação, deve-se levar em consideração o seguinte:

-"g”Tem um valor constante que em média é 9,8 m / s^dois ou cerca de 10 m / s^dois se preferir para facilitar os cálculos quando muita precisão não é necessária.

-Quando v_ou Certo 0, essas equações se reduzem às de queda livre.

-Se o lançamento for para cima, o objeto precisa ter uma velocidade inicial que permita seu movimento. Uma vez em movimento, o objeto atinge uma altura máxima que dependerá de quão grande é a velocidade inicial. Obviamente, quanto maior a altitude, mais tempo o celular passará no ar.

-O objeto retorna ao ponto inicial com a mesma velocidade com que foi lançado, mas a velocidade é direcionada para baixo.

-Para um lançamento vertical descendente, quanto maior a velocidade inicial, mais cedo o objeto atingirá o solo. Aqui, a distância percorrida é definida de acordo com a altura selecionada para o lançamento.

-No lance vertical para cima, o tempo que leva para o celular atingir a altura máxima é calculado fazendo v = 0 na equação 2) da seção anterior. Este é ele tempo máximo t_max:

0 = v_ou - g. t_max ⇒ t_max = v_ou / g

-O altura máxima Y_max é eliminado da equação 3) da seção anterior, fazendo o mesmo v = 0:

0 = v_ou^dois - 2 g. Δy ⇒ 0 = v_ou^dois - 2 g. (Y_max - Y_ou) ⇒ e_max = e_ou  + v_ou^dois / 2 g

sim Y_ou = 0, É reduzido a:

Y_max = v_ou^dois / 2 g

Exemplo trabalhado 1

Uma bola é lançada verticalmente para cima com v_ou = 14 m / s, do topo de um edifício de 18 m de altura. A bola pode continuar seu caminho até a calçada. Calcular:

a) A altura máxima atingida pela bola em relação ao solo.

b) O tempo que estava no ar (hora do voo).

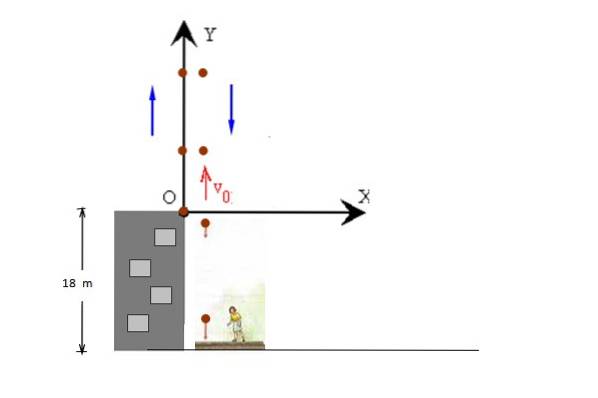
Solução

A figura mostra os movimentos de levantamento e abaixamento da bola separadamente para maior clareza, mas ambos ocorrem ao longo da mesma linha. A posição inicial é tomada em y = 0, de modo que a posição final é y = - 18 m.

a) A altura máxima medida a partir do telhado do edifício é Y_max = v_ou^dois / 2 g e a partir da declaração podemos ler que a velocidade inicial é +14 m / s, então:

Y_max = (14 m / s)^dois / 2 x 9,8 m / s^dois = 10 m (Em relação ao telhado)

H_max = 10 m + 18 m = 28 m (Em relação à calçada).

b) Para encontrar o tempo total ou hora do voo a bola fica no ar, a equação será usada y = y_ou + v_ou.t - ½ g.t^dois, com os seguintes valores e sinais:

y = - 18 m

Y_ou = 0 m

v_ou = +14 m / s

Substituindo:

- 18 = 14.t - ½ 9,8 .t^dois

- 4,9 t^dois+14.t + 18 = 0 

4,9 t^dois-14.t - 18 = 0

É uma equação de segundo grau que se resolve facilmente com a ajuda de uma calculadora científica ou com o solucionador. As soluções são: 3,82 e -0,96. A solução negativa é descartada, pois, por ser um tempo, falta-lhe sentido físico.

O tempo de vôo da bola é 3,82 segundos.

Exemplo trabalhado 2

Uma partícula carregada positivamente com q = +1,2 milicoulombs (mC) e massa m = 2,3 x 10 ^-10 Kg é projetado verticalmente para cima, a partir da posição mostrada na figura e com velocidade inicial v_ou = 30 km / s.

Entre as placas carregadas existe um campo elétrico E uniforme, direcionado verticalmente para baixo e com magnitude de 780 N / C. Se a distância entre as placas for de 18 cm, a partícula irá colidir com a placa superior? Negligencie a atração gravitacional na partícula, pois ela é extremamente leve.

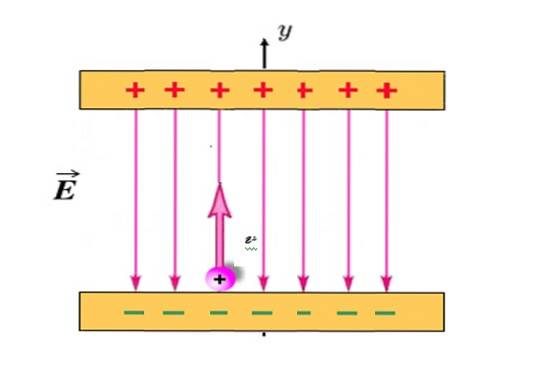
Solução

Neste problema, o campo elétrico E é aquele que produz uma força F e a conseqüente aceleração. Com carga positiva, a partícula é sempre atraída para a placa inferior, porém quando projetada verticalmente para cima atingirá uma altura máxima e retornará para a placa inferior, assim como a bola dos exemplos anteriores..

Por definição de campo elétrico:

E = F / q = m.a / q ⇒ a = q.E / m

Você precisa usar esta equivalência antes de substituir valores:

1 mC = 1 x 10^-3 C

Assim, a aceleração é:

a = 1,2 x 10^-3 x 780 / 2,3 x 10 ^-10em^dois = 4,07 x 10⁹ em^dois

Para a altura máxima, a fórmula da seção anterior é usada, mas em vez de usar “g”Este valor de aceleração é usado:

Y_max = v_ou^dois / 2a = (30.000 m / s)^dois/ 2 x 4,07 x 10⁹ em^dois = 0,11m = 11cm

Não colide com a placa superior, pois está a 18 cm do ponto inicial, e a partícula atinge apenas 11 cm.

Referências

1. Kirkpatrick, L. 2007. Physics: A Look at the World. 6^ta Edição reduzida. Cengage Learning. 23-27.
2. Rex, A. 2011. Fundamentals of Physics. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14^º. Ed. Volume 1. 50 - 53.
4. Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9^{n / D} Ed. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Physics 10. Pearson Education. 133 - 149.