
Propriedades, aplicativos, exemplos da transformada de Fourier
O transformada de Fourier é um método de adequação analítica orientado para funções integráveis que pertence à família de ttransformado integralmente. Consiste em uma redefinição de funções F (t) em termos de Cos (t) e Sen (t).
As identidades trigonométricas dessas funções, juntamente com suas características de derivação e antiderivação, servem para definir a transformada de Fourier por meio da seguinte função complexa:
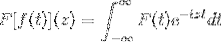
O que é verdade, desde que a expressão faça sentido, isto é, quando a integral imprópria é convergente. Algebricamente, a transformada de Fourier é considerada um homeomorfismo linear.
Toda função que pode ser trabalhada com uma transformada de Fourier deve apresentar nulo fora de um parâmetro definido.
Índice do artigo
- 1 propriedades
- 1.1 Existência
- 1.2 Linearidade da transformação de Fourier
- 1.3 Transformada de Fourier de uma derivada
- 1.4 Diferenciação da transformada de Fourier
- 1.5 Transformada de Fourier de uma tradução
- 1.6 Tradução da transformada de Fourier
- 1.7 Transformada de Fourier de um grupo de escala
- 1.8 Simetria
- 1.9 Transformada de Fourier de um produto de convolução
- 1,10 Continuidade e decadência ao infinito
- 2 História
- 3 Para que serve a transformada de Fourier?
- 3.1 A série Fourier
- 3.2 Outras formas da série de Fourier
- 4 aplicativos
- 4.1 Cálculo da solução fundamental
- 4.2 Teoria do sinal
- 5 exemplos
- 5.1 Exemplo 1
- 5.2 Exemplo 2
- 6 exercícios propostos
- 7 referências
Propriedades

A transformação de Fourier atende às seguintes propriedades:
Existência
Verificar a existência da transformada de Fourier em uma função f (t) definida em reais R, os 2 axiomas a seguir devem ser cumpridos:
- f (t) é contínuo por partes para tudo R
- f (t) é integrável em R
Linearidade da transformação de Fourier
Sejam M (t) e N (t) quaisquer duas funções com transformadas de Fourier definidas, com quaisquer constantes a e b.
F [a M (t) + b N (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)
Que também é apoiado pela linearidade da integral de mesmo nome.
Transformada de Fourier de uma derivada
Tem uma função F que é contínuo e integrável em todos os reais, onde:
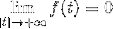
E a derivada de f (f ') é contínua e definida aos poucos ao longo de R
A transformada de Fourier de uma derivada é definida pela integração por partes, pela seguinte expressão:
F [f '(t)] (z) = izF [f (t)] (z)
Nas derivações de ordem superior, será aplicado de forma homóloga, onde para todo n 1 temos:
F [f n'(t)] (z) = (iz)nF [f (t)] (z)
Diferenciação da transformada de Fourier
Tem uma função F que é contínuo e integrável em todos os reais, onde:
i (d / dz)F [f (t)] (z) = F [t. f (t)] (z)
Transformada de Fourier de uma tradução
Para tudo θ que pertence a um conjunto S e T que pertence ao conjunto S ', temos:
F [ τpara θ] = e-iay F [ θ] F [ τparaT ] = e-iax F [ T]
Com τpara trabalhando como o operador de tradução no vetor a.
Tradução da transformada de Fourier
Para tudo θ que pertence a um conjunto S e T que pertence ao conjunto S ', temos:
τpara F [θ] = F [e-iax.θ] τpara F [T ] = F [e-iay . T]
Para tudo para que pertence a R
Transformada de Fourier de um grupo de escala
Para tudo θ que pertence a um conjunto S. T que pertence ao conjunto S '
λ pertencente a R - 0 se tem que:
F [θ (λx)] = (1 / | λ |) F [θ] (Y /λ)
F [T (λx)] = (1 / | λ |) F [T] (y / λ)
sim F é uma função contínua e claramente integrável, onde a> 0. Então:
F [f (at)] (z) = (1 / a) F [f (t)] (z / a)
Para demonstrar este resultado, podemos prosseguir com a mudança da variável.
Quando T → + então s = em → + ∞
Quando T → - então s = em → - ∞
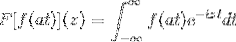
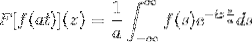
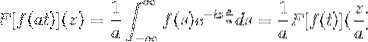
Simetria
Para estudar a simetria da transformada de Fourier, a identidade de Parseval e a fórmula de Plancherel deve ser verificada.
Temos θ e δ que pertencem a S. A partir daí, pode-se deduzir que:
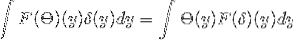
Recebendo
1 / (2π)d F [θ ], F [δ] Identidade de Parseval
1 / (2π)d / 2 || F [θ ] ||eudoisRd Fórmula Plancherel
Transformada de Fourier de um produto de convolução
Perseguindo objetivos semelhantes aos da transformada de Laplace, a convolução de funções refere-se ao produto entre suas transformadas de Fourier..
Temos feg como 2 funções limitadas, definidas e completamente integráveis:
F (f * g) = F (f). F (g)
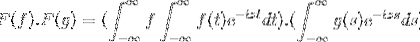
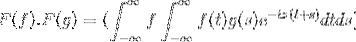
Então, ao mudar a variável
t + s = x; continua com o integral duplo impróprio
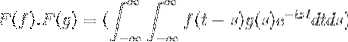
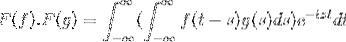
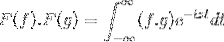
F (f). F (g) = F (f. G)
Continuidade e queda no infinito
Para tudo θ que pertence a R, F [ θ] obedece aos critérios de uma função contínua limitada em Rd.
Também F [ θ] (y) → 0 em C se | y | → ∞
História
Este conceito matemático foi apresentado por Joseph B. Fourier em 1811 ao desenvolver um tratado sobre o propagação de calor. Foi rapidamente adotado por vários ramos da ciência e da engenharia.
Estabeleceu-se como principal ferramenta de trabalho no estudo de equações com derivadas parciais, mesmo comparando-a com a relação de trabalho existente entre as Transformada de Laplace e equações diferenciais ordinárias.
Para que serve a transformada de Fourier?
Ele serve principalmente para simplificar significativamente as equações, enquanto transforma expressões derivadas em elementos de potência, denotando expressões diferenciais na forma de polinômios integráveis..
Na otimização, modulação e modelagem de resultados, atua como uma expressão padronizada, sendo um recurso frequente para a engenharia após várias gerações..
A série Fourier
São séries definidas em termos de cossenos e senos; Eles servem para facilitar o trabalho com funções periódicas gerais. Quando aplicados, fazem parte das técnicas de resolução de equações diferenciais ordinárias e parciais..
As séries de Fourier são ainda mais gerais do que as séries de Taylor, porque desenvolvem funções descontínuas periódicas que não possuem uma representação da série de Taylor..
Outras formas da série Fourier
Para entender a transformada de Fourier analiticamente, é importante revisar as outras maneiras pelas quais a série de Fourier pode ser encontrada, até que possamos definir a série de Fourier em sua notação complexa..
-Série de Fourier em uma função de período 2L
Muitas vezes é necessário adaptar a estrutura de uma série de Fourier para funções periódicas cujo período é p = 2L> 0 no intervalo [-L, L].
-Série de Fourier em funções ímpares e pares
O intervalo [-π, π] é considerado, o que oferece vantagens ao aproveitar as características simétricas das funções.
Se f for par, a série de Fourier é estabelecida como uma série de cossenos.
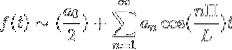
Se f for ímpar, a série de Fourier é estabelecida como uma série de senos.
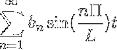
-Notação complexa da série de Fourier
Se tivermos uma função f (t), que atende a todos os requisitos de desenvolvibilidade da série de Fourier, é possível denotá-la no intervalo [-t, t] usando sua notação complexa:
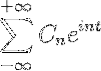
Formulários

Cálculo da solução fundamental
A transformada de Fourier é uma ferramenta poderosa no estudo de equações diferenciais parciais do tipo linear com coeficientes constantes. Eles se aplicam a funções com domínios ilimitados igualmente.
Como a transformada de Laplace, a transformada de Fourier transforma uma função derivada parcial em uma equação diferencial ordinária muito mais simples de operar..
O problema de Cauchy para a equação do calor apresenta um campo de aplicação frequente da transformada de Fourier onde a função é gerada. núcleo de calor ou núcleo de Dirichlet.
Em relação ao cálculo da solução fundamental, são apresentados os seguintes casos em que é comum encontrar a transformada de Fourier:
-Equação de Laplace
-Equação de calor
-Equação de Schrödinger
-Equação de onda
Teoria do sinal
A razão geral para a aplicação da transformada de Fourier neste ramo é principalmente devido à decomposição característica de um sinal como uma superposição infinita de sinais mais facilmente tratáveis.
Pode ser uma onda sonora ou uma onda eletromagnética, a transformada de Fourier expressa isso em uma superposição de ondas simples. Esta representação é bastante frequente na engenharia elétrica.
Por outro lado, existem exemplos da aplicação da transformada de Fourier no campo da teoria dos sinais:
-Problemas de identificação do sistema. Estabelecido f e g
-Problema de consistência do sinal de saída
-Problemas com filtragem de sinal
Exemplos
Exemplo 1
Defina a transformação de Fourier para a seguinte expressão:
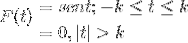
Também podemos representá-lo da seguinte maneira:
F (t) = Sen (t) [H(t + k) - H(t - k) ]
O pulso retangular é definido:
p (t) = H(t + k) - H(t - k)
A transformada de Fourier é aplicada à seguinte expressão que se assemelha ao teorema da modulação.
f (t) = p (t) Sen (t)
Onde: F [w] = (1/2) i [p (w + 1) - p (w - 1)]
E a transformada de Fourier é definida por:
F [w] = (1/2) i [(2 / 2w + 1) Sen (k (w + 1)) - (2 / 2w + 1) Sen (k (w-1))]
Exemplo 2
Defina a transformação de Fourier para a expressão:
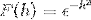
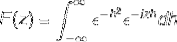
Uma vez que f (h) é uma função par, pode-se afirmar que
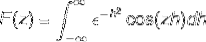
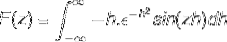
A integração por partes é aplicada selecionando as variáveis e seus diferenciais como segue
u = sin (zh) du = z cos (zh) dh
dv = h (e-h)dois v = (e-h)dois / dois
Substituindo você tem
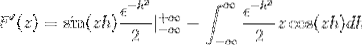
Depois de avaliar sob o teorema fundamental do cálculo
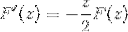
Aplicando o conhecimento prévio sobre equações diferenciais de primeira ordem, a expressão é denotada como
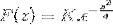
Para obter K avaliamos
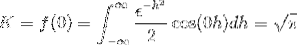
Finalmente, a transformada de Fourier da expressão é definida como
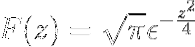
Exercícios propostos
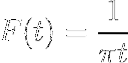
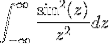
- Obtenha a transformação da expressão W / (1 + wdois)
Referências
- Duoandikoetxea Zuazo, J., Fourier analysis. Addison- Wesley Iberoamericana, Universidade Autônoma de Madrid, 1995.
- Lions, J. L., Análise Matemática e Métodos Numéricos para Ciência e Tecnologia. Springer-Verlag, 1990.
- Lieb, E. H., kernels gaussianos possuem apenas maximizadores gaussianos. Inventar. Matemática. 102, 179-208, 1990.
- Dym, H., McKean, H. P., Fourier Series and Integrals. Academic Press, Nova York, 1972.
- Schwartz, L., Théorie des Distributions. Ed. Hermann, Paris, 1966.



Ainda sem comentários