
Propriedades do trapézio escaleno, fórmulas e equações, exemplos
UMA trapézio escaleno é um polígono com quatro lados, dois dos quais são paralelos entre si, e com seus quatro ângulos internos de diferentes medidas.
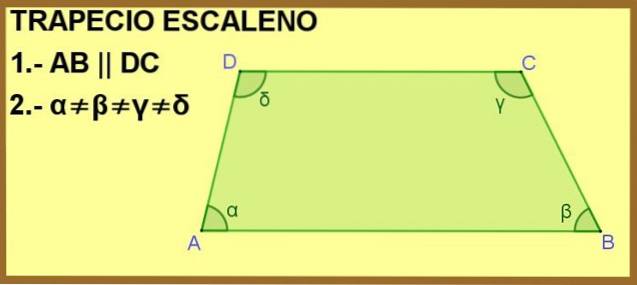
O quadrilátero ABCD é mostrado abaixo, onde os lados AB e DC são paralelos um ao outro. Isso é o suficiente para torná-lo um trapézio, mas além disso, os ângulos internos α, β, γ e δ são todos diferentes, portanto o trapézio é escaleno.
Índice do artigo
- 1 elementos do trapézio escaleno
- 1.1 Outros trapézios
- 2 propriedades
- 3 Fórmulas e equações
- 3.1 Altura
- 3,2 mediana
- 3.3 Diagonais
- 3.4 Perímetro
- 3,5 Área
- 3.6 Outras relações para o trapézio escaleno
- 4 Construção do trapézio escaleno com régua e compasso
- 5 exemplo
- 5.1 - Solução a
- 5.2 - Solução b
- 6 Exercício resolvido
- 6.1 Solução
- 7 referências
Elementos do trapézio escaleno
Aqui estão os elementos mais característicos:
-Bases e lados: os lados paralelos do trapézio são suas bases e os dois lados não paralelos são as laterais.
Em um trapézio escaleno, as bases são de comprimentos diferentes e as laterais também. No entanto, um trapézio escaleno pode ter uma lateral igual em comprimento a uma base..
-Mediana: é o segmento que une os pontos médios das laterais.
-Diagonais: a diagonal de um trapézio é o segmento que une dois vértices opostos. Um trapézio, como todo quadrilátero, tem duas diagonais. No trapézio escaleno, eles são de comprimentos diferentes.
Outros trapézios
Além do trapézio escaleno, existem outros trapézios particulares: o trapézio direito e o trapézio isósceles..
Um trapézio é um retângulo quando um de seus ângulos está correto, enquanto um trapézio isósceles tem seus lados de igual comprimento.
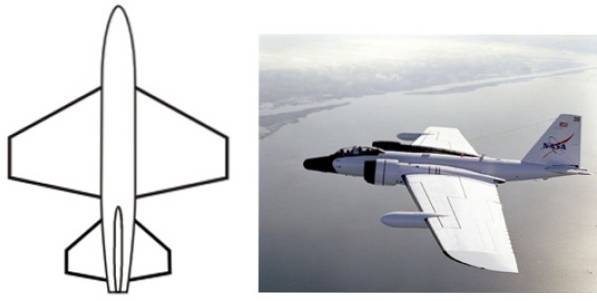
A forma trapezoidal tem inúmeras aplicações em nível de design e indústria, como na configuração de asas de aeronaves, formas de objetos do dia a dia, como mesas, encostos de cadeiras, embalagens, bolsas, estampas têxteis e muito mais..
Propriedades
Listadas abaixo estão as propriedades do trapézio escaleno, muitos dos quais se estendem a outros tipos de trapézio. A seguir, ao se falar em "trapézio", a propriedade será aplicável a qualquer tipo, inclusive o escaleno..
1. A mediana do trapézio, ou seja, o segmento que une os pontos médios de seus lados não paralelos, é paralelo a qualquer uma das bases.
2.- A mediana de um trapézio tem um comprimento que é a semi-soma de suas bases e corta suas diagonais no ponto médio.
3.- As diagonais de um trapézio se cruzam em um ponto que as divide em duas seções que são proporcionais aos quocientes das bases.
4.- A soma dos quadrados das diagonais de um trapézio é igual à soma dos quadrados de seus lados mais o duplo produto de suas bases..
5.- O segmento que une os pontos médios das diagonais tem um comprimento igual à semidiferença das bases.
6.- Os ângulos adjacentes aos laterais são complementares.
7.- Em um trapézio escaleno, o comprimento de suas diagonais são diferentes.
8.- Um trapézio tem uma circunferência inscrita apenas se a soma de suas bases for igual à soma de seus lados.
9.- Se um trapézio tem uma circunferência inscrita, então o ângulo com o vértice no centro da dita circunferência e lados que passam pelas extremidades da lateral do trapézio é reto.
10.- Um trapézio escaleno não tem circunferência circunscrita, o único tipo de trapézio que a tem é o isósceles.
Fórmulas e equações
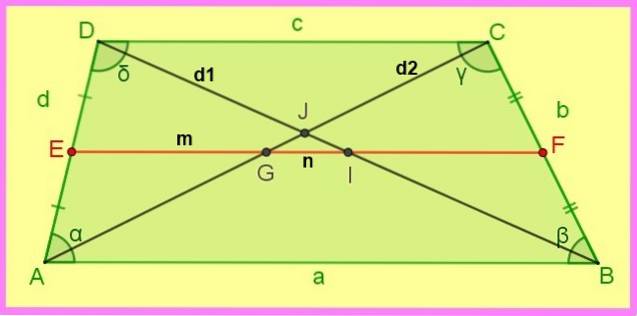
As relações a seguir do trapézio escaleno são referidas na figura a seguir.
1.- Se AE = ED e BF = FC → EF || AB e EF || DC.
2.- EF = (AB + DC) / 2 ou seja: m = (a + c) / 2.
3.- DI = IB = d1 / 2 e AG = GC = ddois /dois.
4.- DJ / JB = (c / a) da mesma forma CJ / JA = (c / a).
5.- DBdois + ACdois = ADdois + ACdois + 2 AB ∙ DC
Equivalentemente:
d1dois + ddoisdois = ddois + bdois + 2 a ∙ c
6.- GI = (AB - DC) / 2
Quer dizer:
n = (a - c) / 2
7.- α + δ = 180⁰ e β + γ = 180⁰
8.- Se α ≠ β ≠ γ ≠ δ então d1 ≠ d2.
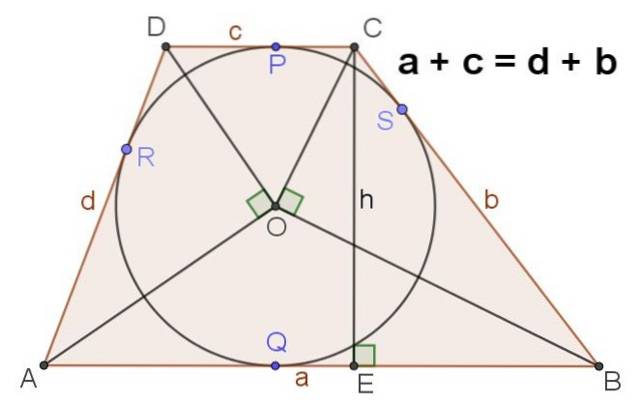
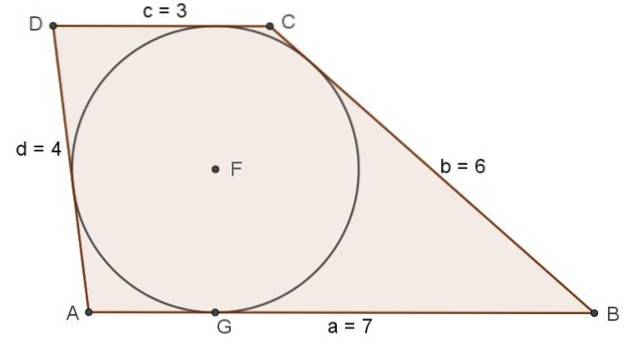
9.- A Figura 4 mostra um trapézio escaleno que tem uma circunferência inscrita, neste caso é verdade que:
a + c = d + b
10.- Em um trapézio escaleno ABCD com uma circunferência inscrita de centro O, o seguinte também é verdadeiro:
∡AOD = ∡BOC = 90⁰
Altura
A altura de um trapézio é definida como o segmento que vai de um ponto da base perpendicularmente à base oposta (ou ao seu prolongamento).
Todas as alturas do trapézio têm a mesma medida h, portanto, na maioria das vezes, a palavra altura se refere à sua medida. Em síntese, a altura é a distância ou separação entre as bases.
A altura h pode ser determinada conhecendo o comprimento de um lado e um dos ângulos adjacentes ao lado:
h = d Sen (α) = d Sen (γ) = b Sen (β) = b Sen (δ)
Mediana
A medida m da mediana do trapézio é a semi-soma das bases:
m = (a + b) / 2
Diagonais
d1 = √ [adois + ddois - 2 ∙ a ∙ d ∙ Cos (α)]
ddois= √ [adois + bdois - 2 ∙ a ∙ b ∙ Cos (β)]
Também pode ser calculado se apenas o comprimento dos lados do trapézio for conhecido:
d1 = √ [bdois + a ∙ c - a (bdois - ddois) / (a - c)]
ddois = √ [ddois + a ∙ c - a (ddois - bdois) / (a - c)]
Perímetro
O perímetro é o comprimento total do contorno, ou seja, a soma de todos os seus lados:
P = a + b + c + d
Área
A área de um trapézio é a semi-soma de suas bases multiplicada por sua altura:
A = h ∙ (a + b) / 2
Também pode ser calculado se a mediana me a altura h forem conhecidas:
A = m ∙ h
Caso apenas o comprimento dos lados do trapézio seja conhecido, a área pode ser determinada usando a fórmula de Heron para o trapézio:
A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]
Onde s é o semiperímetro: s = (a + b + c + d) / 2.
Outras relações para o trapézio escaleno
A intersecção da mediana com as diagonais e o paralelo que passa pela intersecção das diagonais dá origem a outras relações.
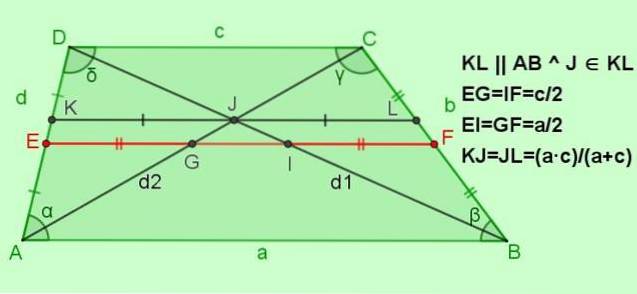
-Relacionamentos para a EF mediana
EF = (a + c) / 2; EG = IF = c / 2; EI = GF = a / 2
-Relações para o segmento paralelo às bases KL, e passando pelo ponto de Intersecção J das diagonais
Se KL || AB || DC com J ∈ KL, então KJ = JL = (a ∙ c) / (a + c)
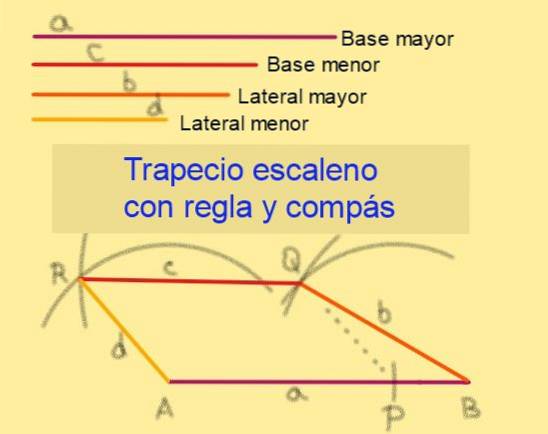
Construção do trapézio escaleno com régua e compasso
Dadas as bases dos comprimentos para Y c, onde a> c e com lados de comprimentos b e d, sendo b> d, prossiga seguindo estas etapas (veja a figura 6):
1.- Com a regra desenha-se o segmento do AB maior.
2.- A partir de A se e em AB o ponto P é marcado de forma que AP = c.
3.- Com a bússola com centro em P e raio d, um arco é desenhado.
4.- Centro em B com o raio b desenhando um arco que intercepta o arco desenhado no passo anterior. Chamamos Q de ponto de intersecção.
5.- Com o centro em A, desenhe um arco de raio d.
6.- Com o centro em Q, desenhe um arco de raio c que intercepta o arco desenhado no passo anterior. O ponto de corte será denominado R.
7.- Os segmentos BQ, QR e RA são traçados com a régua.
8.- O quadrilátero ABQR é um trapézio escaleno, visto que APQR é um paralelogramo que garante que AB || Qr.
Exemplo
Os seguintes comprimentos são dados em cm: 7, 3, 4 e 6.
a) Determine se com eles é possível construir um trapézio escaleno que possa circunscrever um círculo.
b) Encontre o perímetro, a área, o comprimento das diagonais e a altura do referido trapézio, bem como o raio do círculo inscrito.
- Solução para
Usando os segmentos de comprimento 7 e 3 como bases e aqueles de comprimento 4 e 6 como laterais, um trapézio escaleno pode ser construído usando o procedimento descrito na seção anterior.
Resta verificar se possui circunferência inscrita, mas lembrando da propriedade (9):
Um trapézio tem uma circunferência inscrita apenas se a soma de suas bases for igual à soma de seus lados.
Vemos isso de forma eficaz:
7 + 3 = 4 + 6 = 10
Então, a condição de existência da circunferência inscrita é cumprida.
- Solução b
Perímetro
O perímetro P é obtido somando os lados. Como as bases somam 10 e as laterais também, o perímetro é:
P = 20 cm
Área
Para determinar a área, conhecida apenas seus lados, a relação é aplicada:
A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]
Onde s é o semiperímetro:
s = (a + b + c + d) / 2.
No nosso caso, o semiperímetro vale s = 10 cm. Depois de substituir os respectivos valores:
a = 7 cm; b = 6 cm; c = 3 cm; d = 4 cm
Permanece:
A = [10/4] √ [(3) (7) (- 1) (- 3)] = (5/2) √63 = 19,84 cm².
Altura
A altura h está relacionada à área A pela seguinte expressão:
A = (a + c) ∙ h / 2, a partir do qual a altura pode ser obtida por desmatamento:
h = 2A / (a + c) = 2 * 19,84 / 10 = 3,988 cm.
Raio do círculo inscrito
O raio do círculo inscrito é igual a metade da altura:
r = h / 2 = 1.984 cm
Diagonais
Finalmente, o comprimento das diagonais é encontrado:
d1 = √ [bdois + a ∙ c - a (bdois - ddois) / (a - c)]
ddois = √ [ddois + a ∙ c - a (ddois - bdois) / (a - c)]
Substituindo adequadamente os valores, temos:
d1 = √ [6dois + 7 ∙ 3 - 7 (6dois - 4dois) / (7 - 3)] = √ (36 + 21-7 (20) / 4) = √ (22)
ddois = √ [4dois + 7 ∙ 3 - 7 (4dois - 6dois) / (7 - 3)] = √ (16 + 21-7 (-20) / 4) = √ (72)
Ou seja: d1 = 4,69 cm e ddois = 8,49 cm
Exercício resolvido
Determine os ângulos internos do trapézio com bases AB = a = 7, CD = c = 3 e ângulos laterais BC = b = 6, DA = d = 4.
Solução
O teorema do cosseno pode ser aplicado para determinar os ângulos. Por exemplo, o ângulo ∠A = α é determinado a partir do triângulo ABD com AB = a = 7, BD = d2 = 8,49 e DA = d = 4.
O teorema do cosseno aplicado a este triângulo é assim:
ddoisdois = adois + ddois - 2 ∙ a ∙ d ∙ Cos (α), ou seja:
72 = 49 + 16-56 ∙ Cos (α).
Resolvendo para, o cosseno do ângulo α é obtido:
Cos (α) = -1/8
Ou seja, α = ArcCos (-1/8) = 97,18⁰.
Da mesma forma, são obtidos os demais ângulos, sendo seus valores:
β = 41,41⁰; γ = 138,59⁰ e finalmente δ = 82,82⁰.
Referências
- C. E. A. (2003). Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matemática 2. Grupo Editorial Patria.
- Freed, K. (2007). Descubra polígonos. Empresa de Educação de Referência.
- Hendrik, V. (2013). Polígonos generalizados. Birkhäuser.
- IGER. (s.f.). Matemática Primeiro Semestre Tacaná. IGER.
- Geometria Jr. (2014). Polígonos. Lulu Press, Inc.
- Miller, Heeren e Hornsby. (2006). Matemática: Raciocínio e Aplicações (Décima Edição). Pearson Education.
- Patiño, M. (2006). Matemática 5. Editorial Progreso.
- Wikipedia. Trapézio. Recuperado de: es.wikipedia.com


Ainda sem comentários