
Propriedades do trapézio isósceles, relações e fórmulas, exemplos
UMA trapézio isósceles é um quadrilátero em que dois dos lados são paralelos um ao outro e também, os dois ângulos adjacentes a um desses lados paralelos têm a mesma medida.
Na figura 1 temos o quadrilátero ABCD, no qual os lados AD e BC são paralelos. Além disso, os ângulos ∠DAB e ∠ADC adjacentes ao lado paralelo AD têm a mesma medida α.
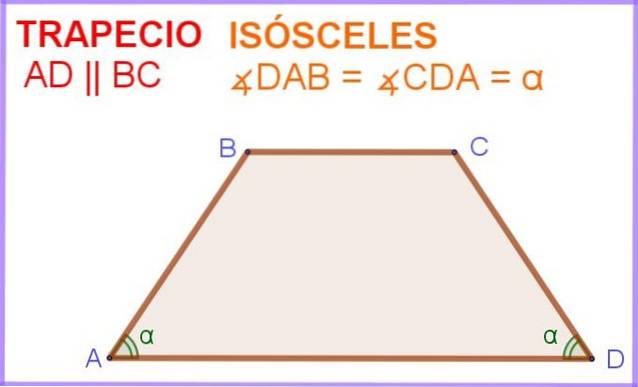
Portanto, este quadrilátero, ou polígono de quatro lados, é na verdade um trapézio isósceles.
Em um trapézio, os lados paralelos são chamados bases e os não paralelos são chamados lateral. Outro recurso importante é o altura, que é a distância que separa os lados paralelos.
Além do trapézio isósceles, existem outros tipos de trapézio:
-Ttamboril escaleno, que tem todos os seus ângulos e lados diferentes.
-Ttamboril retângulo, em que uma lateral tem ângulos adjacentes retos.
A forma trapezoidal é comum em vários campos do design, arquitetura, eletrônica, cálculo e muitos mais, como veremos mais tarde. Daí a importância de se familiarizar com suas propriedades.
Índice do artigo
- 1 propriedades
- 1.1 Exclusivos do trapézio isósceles
- 1.2 Para todos os trapézios
- 2 Relações e fórmulas
- 2.1 Relações únicas do trapézio isósceles
- 2.2 Relações para qualquer trapézio
- 2.3 Relações para trapézio isósceles com circunferência inscrita
- 2.4 Fórmulas para determinar um lado, conhecer os outros e um ângulo
- 2.5 Determinação de um lado, conhecendo os outros e uma diagonal
- 2.6 Base de altura, área e outra base
- 2.7 Bases laterais conhecidas, área e ângulo
- 2.8 Mediana lateral conhecida, área e ângulo
- 2.9 Altura conhecida das laterais
- 2.10 Altura conhecida, ângulo e dois lados
- 2.11 Diagonais conhecidas de todos os lados, ou dois lados e um ângulo
- 2.12 Perímetro do triângulo isósceles
- 2.13 Área do trapézio isósceles
- 2.14 Raio do círculo circunscrito
- 3 Exemplos de uso do trapézio isósceles
- 3.1 Na arquitetura e construção
- 3.2 Em design
- 4 exercícios resolvidos
- 4.1 - Exercício 1
- 4.2 - Exercício 2
- 5 referências
Propriedades
Exclusivo para trapézio isósceles
Se um trapézio é isósceles, ele tem as seguintes propriedades características:
1.- Os lados têm a mesma medida.
2.- Os ângulos adjacentes às bases são iguais.
3.- Ângulos opostos são complementares.
4.- As diagonais têm o mesmo comprimento, sendo iguais os dois segmentos que unem os vértices opostos.
5.- Os ângulos formados entre as bases e as diagonais são todos da mesma medida.
6.- Possui circunferência circunscrita.
Por outro lado, se um trapézio cumprir qualquer uma das propriedades acima, então ele é um trapézio isósceles.
Se em um trapézio isósceles um dos ângulos for reto (90º), então todos os outros ângulos também estarão corretos, formando um retângulo. Ou seja, um retângulo é um caso particular de trapézio isósceles.

Para todos os trapézios
O seguinte conjunto de propriedades é válido para qualquer trapézio:
7.- O mediana do trapézio, ou seja, o segmento que une os pontos médios de seus lados não paralelos, é paralelo a qualquer uma das bases.
8.- O comprimento da mediana é igual à semi-soma (soma dividida por 2) daquela de suas bases.
9.- A mediana de um trapézio corta suas diagonais no ponto médio.
10.- As diagonais de um trapézio se cruzam em um ponto que as divide em duas seções proporcionais aos quocientes das bases.
11.- A soma dos quadrados das diagonais de um trapézio é igual à soma dos quadrados de seus lados mais o duplo produto de suas bases.
12.- O segmento que une os pontos médios das diagonais tem um comprimento igual à semidiferença das bases.
13.- Os ângulos adjacentes aos laterais são complementares.
14.- Um trapézio tem uma circunferência inscrita se e somente se a soma de suas bases for igual à soma de seus lados.
15.- Se um trapézio tem uma circunferência inscrita, então os ângulos com um vértice no centro da referida circunferência e os lados que passam pelas extremidades do mesmo lado são ângulos retos.
Relacionamentos e fórmulas
O seguinte conjunto de relações e fórmulas refere-se à figura 3, onde além do trapézio isósceles são mostrados outros segmentos importantes já mencionados, como diagonais, altura e mediana..
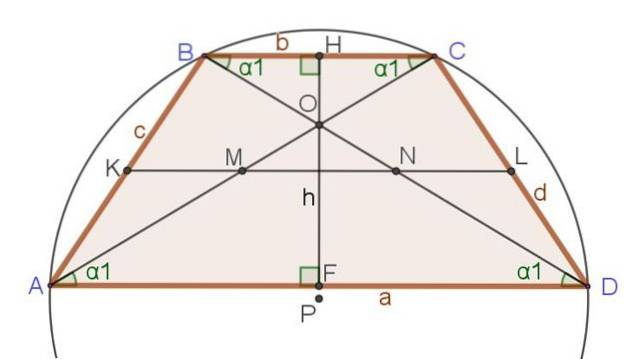
Relações únicas do trapézio isósceles
1.- AB = DC = c = d
2.- ∡DAB = ∡CDA e ∡ABC = ∡BCD
3.- ∡DAB + ∡BCD = 180º e ∡CDA + ∡ABC = 180º
4.- BD = AC
5.- ∡CAD = ∡BDA = ∡CBD = ∡BCA = α1
6.- A, B, C e D pertencem ao círculo circunscrito.
Relacionamentos para qualquer trapézio
- Se AK = KB e DL = LC ⇒ KL || AD e KL || AC
8.- KL = (AD + BC) / 2
9.- AM = MC = AC / 2 e DN = NB = DB / 2
10.- AO / OC = AD / BC e DO / OB = AD / BC
11.- ACdois + DBdois = ABdois + DCdois + 2⋅AD⋅BC
12.- MN = (AD - BC) / 2
13.- ∡DAB + ∡ABC = 180º e ∡CDA + ∡BCD = 180º
14.- Se AD + BC = AB + DC ⇒ ∃ R então equidistante de AD, BC, AB e DC
15.- Se ∃ R equidistante de AD, BC, AB e DC, então:
∡BRA = ∡DRC = 90º
Relações para trapézio isósceles com circunferência inscrita
Se em um trapézio isósceles a soma das bases é igual a duas vezes a lateral, então a circunferência inscrita existe.

As seguintes propriedades se aplicam quando o trapézio isósceles tem uma circunferência inscrita (ver figura 4 acima):
16.- KL = AB = DC = (AD + BC) / 2
17.- As diagonais se cruzam em ângulos retos: AC ⊥ BD
18.- A altura mede a mesma mediana: HF = KL, ou seja, h = m.
19.- O quadrado da altura é igual ao produto das bases: hdois = BC⋅AD
20.- Nestas condições específicas, a área do trapézio é igual ao quadrado da altura ou produto das bases: Área = hdois = BC⋅AD.
Fórmulas para determinar um lado, conhecer os outros e um ângulo
Conhecida uma base, a lateral e um ângulo, a outra base pode ser determinada por:
a = b + 2c Cos α
b = a - 2c Cos α
Se o comprimento das bases e um ângulo são dados como dados conhecidos, os comprimentos de ambos os lados são:
c = (a - b) / (2 Cos α)
Determinação de um lado, conhecendo os outros e uma diagonal
a = (d1dois - cdois) / b;
b = (d1dois - cdois)/ para
c = √ (d1dois - a⋅b)
Onde d1 é o comprimento das diagonais.
Base de altura, área e outra base
a = (2 A) / h - b
b = (2 A) / h - a
Bases laterais conhecidas, área e ângulo
c = (2A) / [(a + b) sen α]
Mediana lateral conhecida, área e ângulo
c = A / (m sin α)
Altura conhecida dos lados
h = √ [4 cdois - (a - b)dois]
Altura conhecida, ângulo e dois lados
h = tg α⋅ (a - b) / 2 = c. sin α
Diagonais conhecidas de todos os lados, ou dois lados e um ângulo
d1 = √ (cdois+ a b)
d1 = √ (adois+ cdois - 2 a c Cos α)
d1 = √ (bdois + cdois- 2 b c Cos β)
Perímetro do triângulo isósceles
P = a + b + 2c
Área do trapézio isósceles
Existem várias fórmulas para o cálculo da área, dependendo dos dados conhecidos. O seguinte é o mais conhecido, dependendo das bases e da altura:
A = h⋅ (a + b) / 2
E você também pode usar estes outros:
-Se os lados são conhecidos
A = [(a + b) / 4] √ [4cdois - (a - b)dois]
-Quando você tem dois lados e um ângulo
A = (b + c Cos α) c Sen α = (a - c Cos α) c Sen α
-Se o raio do círculo inscrito e um ângulo são conhecidos
A = 4 rdois / Sen α = 4 rdois / Sen β
-Quando as bases e um ângulo são conhecidos
A = a⋅b / Sen α = a⋅b / Sen β
-Se o trapézio pode ser inscrito em uma circunferência
A = c⋅√ (a⋅b) = m⋅√ (a⋅b) = r⋅ (a + b) / 2
-Conhecer as diagonais e o ângulo que elas formam entre si
A = (d1dois/ 2) Sen γ = (d1dois / 2) Sen δ
-Quando você tem a lateral, a mediana e um ângulo
A = mc.sen α = mc.sen β
Raio do círculo circunscrito
Apenas os trapézios isósceles têm circunferência circunscrita. Se a base maior a, a lateral c e a diagonal d são conhecidas1, então o raio R do círculo que passa pelos quatro vértices do trapézio é:
R = a⋅c⋅d1 / 4√ [p (p -a) (p-c) (p - d1)]
Onde p = (a + c + d1) / dois
Exemplos de uso do trapézio isósceles
O trapézio isósceles aparece no campo do design, como pode ser visto na Figura 2. E aqui estão alguns exemplos adicionais:
Na arquitetura e construção
Os antigos incas conheciam o trapézio isósceles e o usaram como elemento de construção nesta janela em Cuzco, Peru:

E aqui o trapézio reaparece na chamada folha trapezoidal, um material frequentemente usado na construção:

Em design
Já vimos que o trapézio isósceles aparece em objetos do cotidiano, incluindo alimentos como esta barra de chocolate:

Exercícios resolvidos
- Exercício 1
Um trapézio isósceles tem uma base maior que 9 cm, uma base menor que 3 cm e suas diagonais 8 cm cada. Calcular:
a parte, de lado
b) Altura
c) Perímetro
d) Área
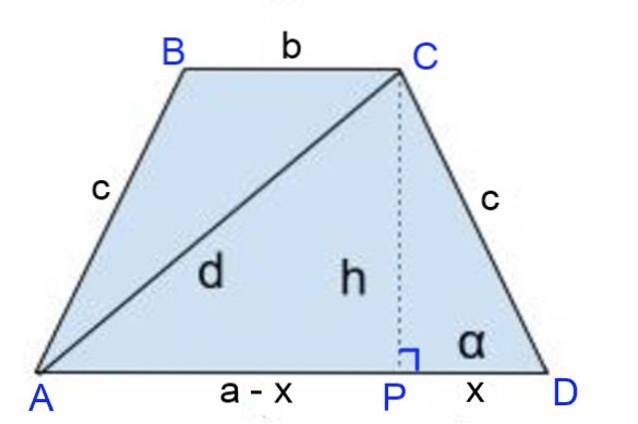
Solução para
A altura CP = h é traçada, onde o pé da altura define os segmentos:
PD = x = (a-b) / 2 y
AP = a - x = a - a / 2 + b / 2 = (a + b) / 2.
Usando o teorema de Pitágoras para o triângulo retângulo DPC:
cdois = hdois + (a - b)dois / 4
E também para o triângulo retângulo APC:
ddois = hdois + APdois = hdois + (a + b)dois / 4
Finalmente, membro por membro, a segunda equação é subtraída da primeira e simplificada:
ddois - cdois = ¼ [(a + b)dois - (a-b)dois] = ¼ [(a + b + a-b) (a + b-a + b)]
ddois - cdois = ¼ [2a 2b] = a b
cdois= ddois - a b ⇒ c = √ (ddois - a b) = √ (8dois - 9⋅3) = √37 = 6,08 cm
Solução b
hdois = ddois - (a + b)dois / 4 = 8dois - (12dois / doisdois ) = 8dois - 6dois = 28
h = 2 √7 = 5,29 cm
Solução c
Perímetro = a + b + 2 c = 9 + 3 + 2⋅6,083 = 24,166 cm
Solução d
Área = h (a + b) / 2 = 5,29 (12) / 2 = 31,74 cm
- Exercício 2
Existe um trapézio isósceles cuja base maior é duas vezes a menor e sua base menor é igual à altura, que é de 6 cm. Decidir:
a) O comprimento da lateral
b) Perímetro
c) Área
d) Ângulos
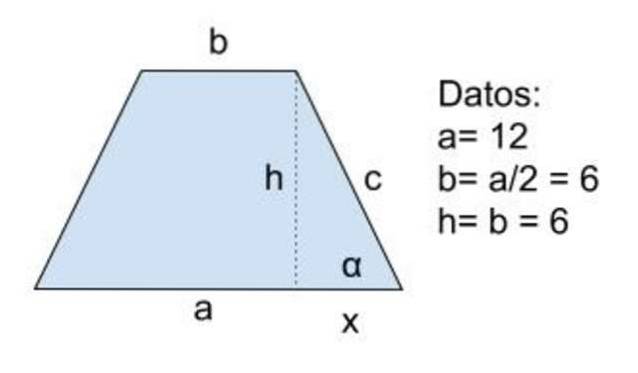
Solução para
Dados: a = 12, b = a / 2 = 6 e h = b = 6
Procedemos desta forma: a altura h é desenhada e o teorema de Pitágoras é aplicado ao triângulo de hipotenusa “c” e pernas he x:
cdois = hdois+xcdois
Então você tem que calcular o valor da altura a partir dos dados (h = b) e da perna x:
a = b + 2 x ⇒ x = (a-b) / 2
Substituindo as expressões anteriores, temos:
cdois = bdois+(a-b)dois/doisdois
Agora os valores numéricos são introduzidos e são simplificados:
cdois = 62+ (12-6) 2/4
cdois = 62 (1 + ¼) = 62 (5/4)
Obtendo:
c = 3√5 = 6,71 cm
Solução b
O perímetro P = a + b + 2 c
P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm
Solução c
A área em função da altura e comprimento das bases é:
A = h⋅ (a + b) / 2 = 6⋅ (12 + 6) / 2 = 54 cmdois
Solução d
O ângulo α formado pela lateral com a base maior é obtido por trigonometria:
Tan (α) = h / x = 6/3 = 2
α = ArcTan (2) = 63,44º
O outro ângulo, aquele que forma a lateral com a base menor, é o β, que é complementar ao α:
β = 180º - α = 180º - 63,44º = 116,56º
Referências
- E. A. 2003. Elementos de geometria: com exercícios e geometria de compasso. Universidade de Medellin.
- Campos, F. 2014. Matemática 2. Grupo Editorial Patria.
- Freed, K. 2007. Discover Polygons. Empresa de Educação de Referência.
- Hendrik, V. 2013. Generalized Polygons. Birkhäuser.
- IGER. Matemática Primeiro Semestre Tacaná. IGER.
- Geometria Jr. 2014. Polygons. Lulu Press, Inc.
- Miller, Heeren e Hornsby. 2006. Mathematics: Reasoning And Applications. 10º. Edição. Pearson Education.
- Patiño, M. 2006. Mathematics 5. Editorial Progreso.
- Wikipedia. Trapézio. Recuperado de: es.wikipedia.com
Ainda sem comentários