
Propriedades do trapézio certo, relações e fórmulas, exemplos
UMA trapézio retângulo é uma figura plana com quatro lados, de modo que dois deles são paralelos entre si, chamada bases e também um dos outros lados é perpendicular às bases.
Por isso, dois dos ângulos internos estão corretos, ou seja, medem 90º. Daí o nome "retângulo" dado à figura. A imagem a seguir de um trapézio direito esclarece essas características:
Índice do artigo
- 1 elementos do trapézio
- 2 Relações e fórmulas
- 2.1 Altura h do trapézio
- 2.2 Perímetro P
- 2.3 Base média
- 2.4 Área
- 2.5 Diagonais, lados e ângulos
- 3 exemplos de trapézios direitos
- 3.1 O trapézio como elemento de design
- 3.2 Gerador de onda trapezoidal
- 3.3 Em cálculo numérico
- 3.4 Feixe com carga trapezoidal
- 3.5 Como uma ferramenta educacional e de aprendizagem
- 4 exercícios resolvidos
- 4.1 - Exercício 1
- 4.2 - Exercício 2
- 5 referências
Elementos do trapézio
Os elementos do trapézio são:
-Bases
-Vértices
-Altura
-Ângulos internos
-Base média
-Diagonais
Detalharemos esses elementos com o auxílio das figuras 1 e 2:
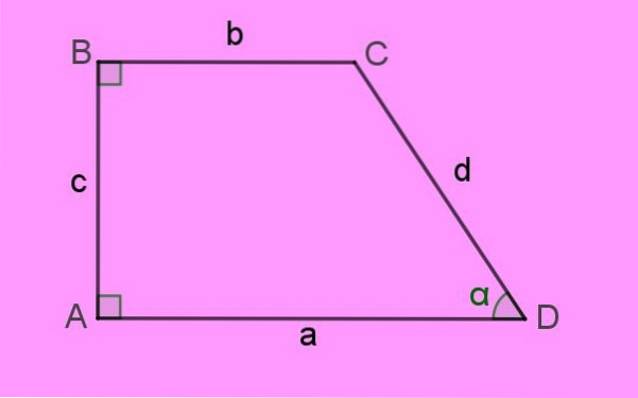
Os lados do trapézio direito são denotados por letras minúsculas a, b, c e d. Os cantos da figura o vértices Eles são indicados em letras maiúsculas. Finalmente, o ângulos internos Eles são expressos em letras gregas.
Por definição, bases deste trapézio estão os lados aeb, que, como pode ser visto, são paralelos e também possuem comprimentos diferentes.
O lado perpendicular a ambas as bases é o lado c à esquerda, que é o altura h do trapézio. E finalmente há o lado d, que forma o ângulo agudo α com o lado a.
A soma do ângulos internos de um quadrilátero é 360º. É facilmente apreciado que o ângulo ausente C na figura é 180 - α.
O base do meio é o segmento que une os pontos médios dos lados não paralelos (segmento EF na figura 2).
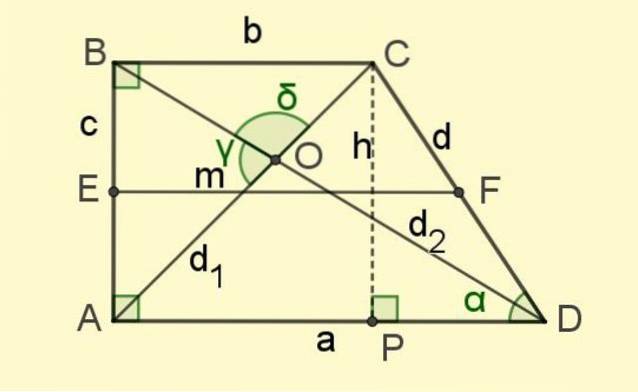
E finalmente existem as diagonais d1 e ddois, os segmentos que unem os vértices opostos e se cruzam no ponto O (ver figura 2).
Relacionamentos e fórmulas
Altura do trapézio h
h = c
Perímetro P
É a medida do contorno e é calculada somando os lados:
Perímetro = a + b + c + d
O lado d é expresso em termos de altura ou lado c usando o teorema de Pitágoras:
d = √ (a-b)dois + cdois
Substituindo no perímetro:
P = a + b + c + √ (a-b)dois + cdois
Base média
É a semi-soma das bases:
Base média = (a + b) / 2
Às vezes, a base média é encontrada expressa desta forma:
Base média = (base principal + base secundária) / 2
Área
A área A do trapézio é o produto da base média vezes a altura:
A = (Base principal + base secundária) x altura / 2
A = (a + b) c / 2
Diagonais, lados e ângulos
Vários triângulos aparecem na Figura 2, direitos e não direitos. O teorema de Pitágoras pode ser aplicado àqueles que são triângulos retângulos e àqueles que não são, os teoremas do cosseno e do seno.
Desta forma, as relações são encontradas entre os lados e entre os lados e os ângulos internos do trapézio..
Triângulo CPA
É um retângulo, suas pernas são iguais e valem b, enquanto a hipotenusa é a diagonal d1, portanto:
d1dois = bdois + bdois = 2bdois
Triângulo DAB
Também é um retângulo, as pernas são para Y c (ou também para Y h) e a hipotenusa é ddois, de maneira que:
ddoisdois = adois + cdois = adois + hdois
Triângulo CDA
Uma vez que este triângulo não é um triângulo retângulo, o teorema do cosseno é aplicado a ele, ou também o teorema do seno.
De acordo com o teorema do cosseno:
d1dois = adois + ddois - 2ad cos α
Triângulo CDP
Este triângulo é um triângulo retângulo e com seus lados as razões trigonométricas do ângulo α são construídas:
sin α = h / d
cos α = PD / d
Mas o lado PD = a - b, portanto:
cos α = (a-b) / d → a - b = d cos α
a = b + d cos α
Você também tem:
tg α = sin α / cos α = h / (a-b) → h = tg α (a-b)
Triângulo CBD
Neste triângulo temos o ângulo cujo vértice está em C. Não está marcado na figura, mas no início foi destacado que é 180 - α. Este triângulo não é um triângulo retângulo, então o teorema do cosseno ou teorema do seno pode ser aplicado..
Agora, pode ser facilmente mostrado que:
sin (180 - α) = sin α
cos (180 - α) = - cos α
Aplicando o teorema do cosseno:
ddoisdois = ddois + bdois - 2 db cos (180 - α) = ddois + bdois + 2db cos α
Exemplos de trapézios direitos
Os trapézios e, em particular, os trapézios direitos são encontrados em muitos lados, e às vezes nem sempre de forma tangível. Aqui temos vários exemplos:
O trapézio como elemento de design
Figuras geométricas abundam na arquitetura de muitos edifícios, como esta igreja em Nova York, que mostra uma estrutura em forma de trapézio retangular.
Da mesma forma, a forma trapezoidal é frequente na concepção de recipientes, recipientes, lâminas (cortador ou exato), emblemas e em design gráfico.

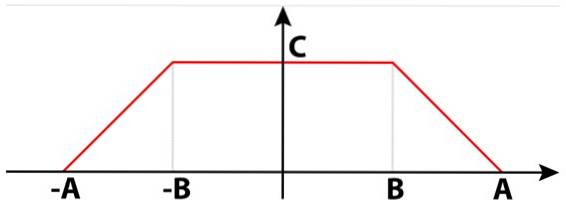
Gerador de onda trapezoidal
Os sinais elétricos não podem ser apenas quadrados, sinusoidais ou triangulares. Existem também sinais trapezoidais que são úteis em muitos circuitos. Na figura 4 há um sinal trapezoidal composto por dois trapézios direitos. Entre eles, eles formam um único trapézio isósceles.
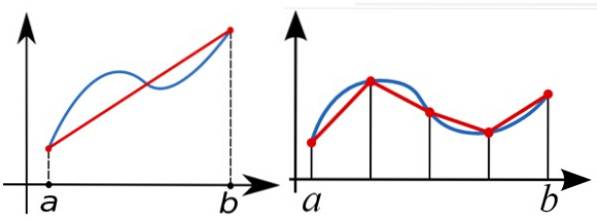
Em cálculo numérico
Para calcular a integral definida da função f (x) entre aeb numericamente, a regra do trapézio é usada para aproximar a área sob o gráfico de f (x). Na figura a seguir, à esquerda, a integral é aproximada com um único trapézio direito.
A melhor aproximação é a da figura da direita, com vários trapézios à direita.
Feixe com carga trapezoidal
As forças nem sempre se concentram em um único ponto, pois os corpos sobre os quais atuam têm dimensões apreciáveis. É o caso de uma ponte sobre a qual circulam continuamente veículos, a água de uma piscina nas paredes verticais da mesma ou um telhado onde se acumula água ou neve..
Por esse motivo, as forças são distribuídas por unidade de comprimento, área de superfície ou volume, dependendo do corpo sobre o qual atuam..
No caso de uma viga, uma força distribuída por unidade de comprimento pode ter várias distribuições, por exemplo, o trapézio direito mostrado abaixo:
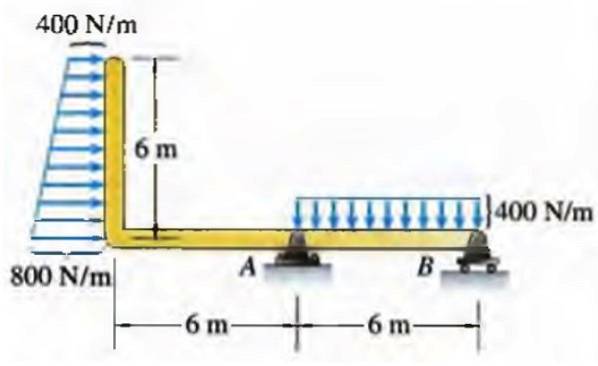
Na realidade, as distribuições nem sempre correspondem a formas geométricas regulares como esta, mas podem ser uma boa aproximação em muitos casos..
Como ferramenta educacional e de aprendizagem
Blocos e imagens com formas geométricas, incluindo trapézios, são muito úteis para as crianças se familiarizarem com o fascinante mundo da geometria desde cedo..

Exercícios resolvidos
- Exercício 1
No trapézio direito da figura 1, a base maior tem 50 cm e a base menor é igual a 30 cm, também se sabe que o lado oblíquo tem 35 cm. Achar:
a) Ângulo α
b) Altura
c) Perímetro
d) Base média
e) Área
f) Diagonais
Solução para
Os dados da declaração são resumidos da seguinte forma:
a = base principal = 50 cm
b = base menor = 30 cm
d = lado inclinado = 35 cm
Para encontrar o ângulo α, visitamos a seção de fórmulas e equações para ver qual se adapta melhor aos dados fornecidos. O ângulo procurado é encontrado em vários dos triângulos analisados, por exemplo, o CDP.
Aí temos esta fórmula, que contém o desconhecido e também os dados que conhecemos:
cos α = (a-b) / d
Portanto:
α = arcos [(a-b) / d] = arcos [(50-30) / 35] = arcos 20/35 = 55,15 º
Solução b
Da equação:
sin α = h / d
Limpa h:
h = d. sen α = 35 sen 55,15 º cm = 28,72 cm
Solução c
O perímetro é a soma dos lados e, como a altura é igual ao lado c, temos:
c = h = 28,72 cm
Portanto:
P = (50 + 30 + 35 + 28,72) cm = 143,72 cm
Solução d
A base média é a semi-soma das bases:
Base média = (50 + 30 cm) / 2 = 40 cm
Solução e
A área do trapézio é:
A = base média x altura = 40 cm x 28,72 = 1148,8 cmdois.
Solução f
Para a diagonal d1 você pode usar esta fórmula:
d1dois = bdois + bdois = 2bdois
d1dois= 2 x (30 cm)dois = 1800 cmdois
d1 = √1800 cmdois = 42,42 cm
E para a diagonal ddois:
ddoisdois = ddois + bdois + 2db cos α = (35 cm)dois + (30 cm)dois + 2 x 35 x 30 cmdois cos 55,15 º = 3325 cmdois
ddois = √ 3325 cmdois = 57,66 cm
Esta não é a única maneira de encontrar ddois, uma vez que há também o triângulo DAB.
- Exercício 2
O gráfico a seguir da velocidade em função do tempo pertence a um móvel que tem movimento retilíneo uniformemente acelerado. Calcule a distância percorrida pelo celular durante o intervalo de tempo entre 0,5 e 1,2 segundos.
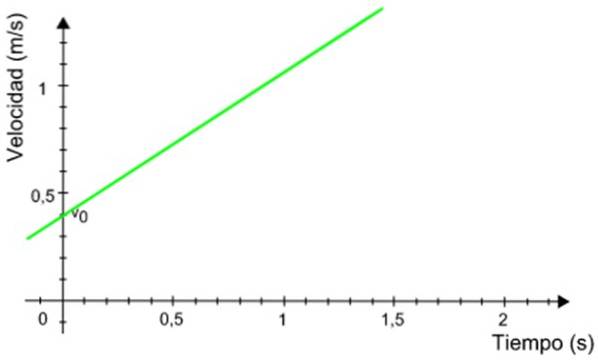
Solução
A distância percorrida pelo celular é numericamente equivalente à área sob o gráfico, delimitada pelo intervalo de tempo indicado.
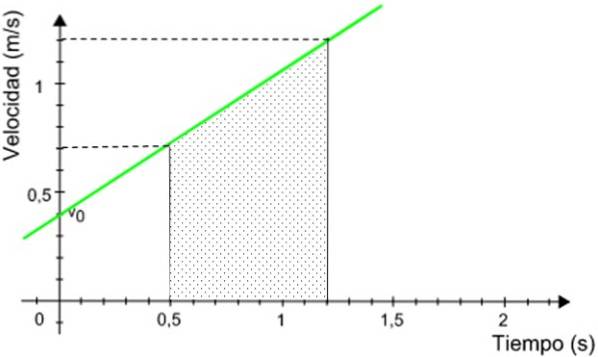
A área sombreada é a área de um trapézio direito, dada por:
A = (Base principal + base secundária) x altura / 2
A = (1,2 + 0,7) m / s x (1,2 - 0,5) s / 2 = 0,665 m
Referências
- Baldor, A. 2004. Geometria plana e espacial com trigonometria. Publicações Culturais.
- Bedford, A. 1996. Statics. Addison Wesley Interamericana.
- Geometria Jr. 2014. Polygons. Lulu Press, Inc.
- OnlineMSchool. Trapézio retangular. Recuperado de: es.onlinemschool.com.
- Solucionador automático de problemas de geometria. O trapézio. Recuperado de: scuolaelettrica.it
- Wikipedia. Trapézio (geometria). Recuperado de: es.wikipedia.org.



Ainda sem comentários