
Características do triângulo equilateral, propriedades, fórmulas, área
UMA Triângulo equilátero é um polígono com três lados, onde todos são iguais; ou seja, eles têm a mesma medida. Para esta característica foi dado o nome de equilátero (lados iguais).
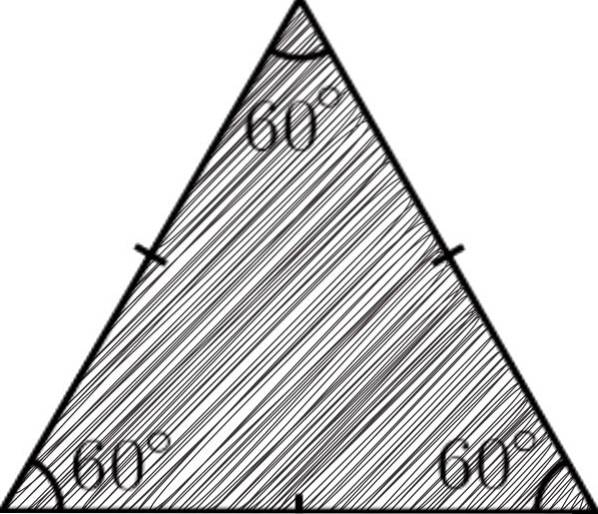
Os triângulos são polígonos considerados os mais simples em geometria, porque são compostos de três lados, três ângulos e três vértices. No caso do triângulo equilátero, por ter lados iguais, isso implica que seus três ângulos também serão iguais..
Índice do artigo
- 1 Características dos triângulos equiláteros
- 1.1 - Lados iguais
- 1.2 - Componentes
- 2 propriedades
- 2.1 ângulos internos
- 2.2 Ângulos externos
- 2.3 Soma dos lados
- 2.4 Lados congruentes
- 2,5 ângulos congruentes
- 3 Como calcular o perímetro?
- 4 Como calcular a altura?
- 5 Como calcular os lados?
- 6 Como calcular a área?
- 7 exercícios
- 7.1 - Primeiro exercício
- 7.2 - Segundo exercício
- 7.3 - Terceiro exercício
- 8 referências
Características dos triângulos equiláteros
- Lados iguais
Os triângulos equilaterais são figuras planas e fechadas, compostas por três segmentos de linha. Os triângulos são classificados por suas características, em relação aos seus lados e ângulos; o equilátero foi classificado usando a medida de seus lados como parâmetro, uma vez que estes são exatamente iguais, ou seja, são congruentes.
O triângulo equilátero é um caso particular do triângulo isósceles porque dois de seus lados são congruentes. É por isso que todos os triângulos equiláteros também são isósceles, mas nem todos os triângulos isósceles serão equiláteros.
Desta forma, os triângulos equiláteros têm as mesmas propriedades de um triângulo isósceles..
Os triângulos equilaterais também podem ser classificados pela largura de seus ângulos internos como um triângulo agudo equilátero, que possui três lados e três ângulos internos com a mesma medida. Os ângulos serão agudos, ou seja, serão menores que 90ou.
- Componentes (editar)
Os triângulos em geral possuem várias linhas e pontos que os compõem. Eles são usados para calcular a área, os lados, os ângulos, a mediana, a bissetriz, a bissetriz e a altura..
- Mediana: é uma linha que começa do ponto médio de um lado e atinge o vértice oposto. As três medianas convergem em um ponto denominado baricentro ou centróide..
- Bisector: é um raio que divide o ângulo dos vértices em dois ângulos de igual medida, por isso é conhecido como eixo de simetria. O triângulo equilátero tem três eixos de simetria. No triângulo equilátero, a bissetriz é desenhada do vértice de um ângulo para seu lado oposto, cortando-o em seu ponto médio. Eles se encontram em um ponto chamado de incentivo.
- A mediadora: é um segmento perpendicular ao lado do triângulo que tem sua origem no meio dele. Existem três mediatices em um triângulo e eles se encontram em um ponto chamado circuncentro.
- A altura: é a linha que vai do vértice ao lado oposto e também esta linha é perpendicular a esse lado. Todos os triângulos têm três alturas que coincidem em um ponto denominado ortocentro..
No gráfico a seguir, vemos um triângulo escaleno onde alguns dos componentes mencionados são detalhados
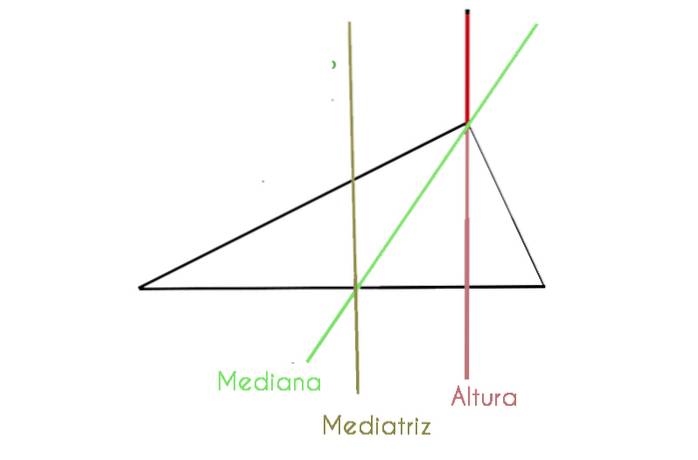
A bissetriz, mediana e bissetriz são coincidentes
A bissetriz divide o lado de um triângulo em duas partes. Nos triângulos equiláteros esse lado será dividido em duas partes exatamente iguais, ou seja, o triângulo será dividido em dois triângulos retângulos congruentes.
Assim, a bissetriz desenhada de qualquer ângulo de um triângulo equilátero coincide com a mediana e a bissetriz do lado oposto a esse ângulo..
Exemplo:
A figura a seguir mostra o triângulo ABC com um ponto médio D que divide um de seus lados em dois segmentos AD e BD.
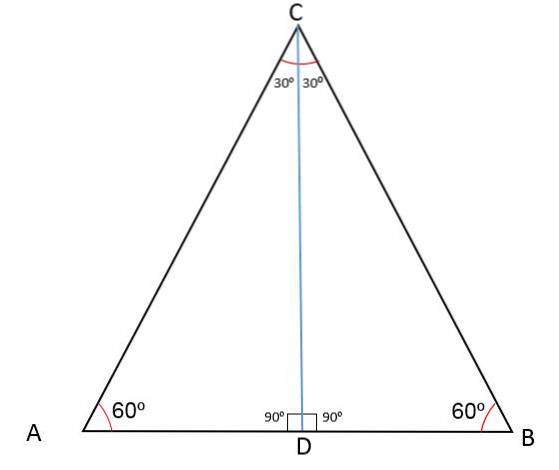
Ao traçar uma linha do ponto D ao vértice oposto, por definição o CD mediano é obtido, que é relativo ao vértice C e ao lado AB.
Como o segmento CD divide o triângulo ABC em dois triângulos iguais CDB e CDA, isso significa que o caso de congruência será tido: lado, ângulo, lado e, portanto, CD também será a bissetriz de BCD.
A plotagem do segmento CD divide o ângulo do vértice em dois ângulos iguais de 30ou, o ângulo do vértice A ainda mede 60ou e a linha CD forma um ângulo de 90ou em relação ao ponto médio D.
O segmento CD forma ângulos que têm a mesma medida para os triângulos ADC e BDC, ou seja, são complementares de forma que a medida de cada um será:
Med. (ADB) + Med. (ADC) = 180ou
dois * Med. (ADC) = 180ou
Med. (ADC) = 180ou ÷ 2
Med. (ADC) = 90ou.
E então, temos que o segmento CD também é a bissetriz do lado AB.
A bissetriz e a altura são coincidentes
Desenhando a bissetriz do vértice de um ângulo até o ponto médio do lado oposto, ele divide o triângulo equilátero em dois triângulos congruentes.
De tal forma que um ângulo de 90 é formadoou (reto). Isso indica que esse segmento de linha é totalmente perpendicular a esse lado e, por definição, essa linha seria a altura.
Desta forma, a bissetriz de qualquer ângulo de um triângulo equilátero coincide com a altura em relação ao lado oposto desse ângulo..
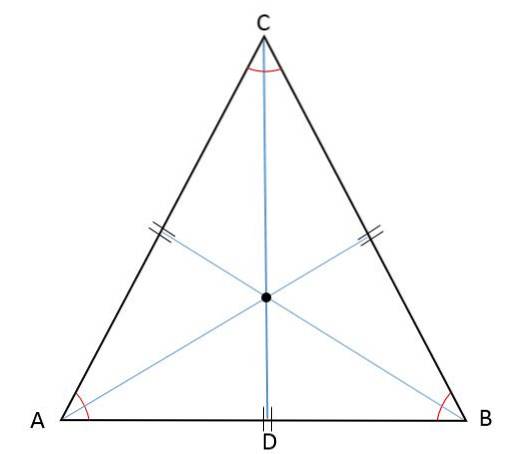
Ortocentro, baricentro, incentivo e circuncentro coincidente
Como a altura, mediana, bissetriz e bissetriz são representadas pelo mesmo segmento ao mesmo tempo, em um triângulo equilátero os pontos de encontro desses segmentos -o ortocentro, bissetriz, incentivo e circuncentro- serão encontrados no mesmo ponto:
Propriedades
A principal propriedade dos triângulos equiláteros é que eles serão sempre triângulos isósceles, uma vez que os isósceles são formados por dois lados congruentes e equiláteros por três..
Desta forma, os triângulos equiláteros herdaram todas as propriedades do triângulo isósceles:
Ângulos internos
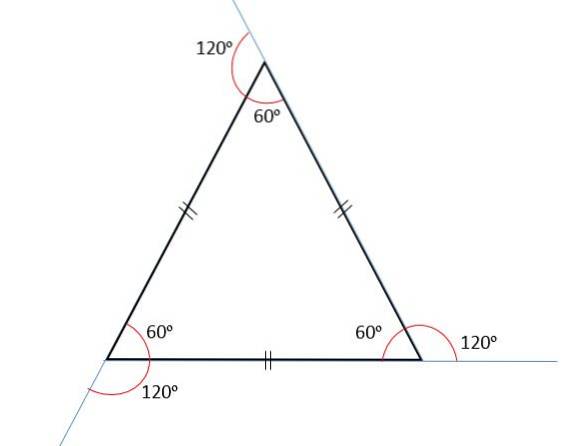
A soma dos ângulos internos é sempre igual a 180ou, e uma vez que todos os seus ângulos são congruentes, cada um deles medirá 60ou.
Ângulos externos
A soma dos ângulos externos sempre será igual a 360ou, portanto, cada ângulo externo medirá 120ou. Isso porque os ângulos internos e externos são complementares, ou seja, ao adicioná-los serão sempre iguais a 180ou.
Soma dos lados
A soma das medidas dos dois lados deve ser sempre maior que a medida do terceiro lado, ou seja, a + b> c, onde a, bec são as medidas de cada lado.
Lados congruentes
Os triângulos equilaterais têm todos os três lados com a mesma medida ou comprimento; ou seja, eles são congruentes. Portanto, no item anterior temos que a = b = c.
Ângulos congruentes
Os triângulos equilaterais também são conhecidos como triângulos equiangulares, porque seus três ângulos internos são congruentes entre si. Isso ocorre porque todos os seus lados também têm a mesma medida.
Como calcular o perímetro?
O perímetro de um polígono é calculado adicionando os lados. Como neste caso o triângulo equilátero tem todos os seus lados com a mesma medida, seu perímetro é calculado com a seguinte fórmula:
P = 3 * lado.
Como calcular a altura?
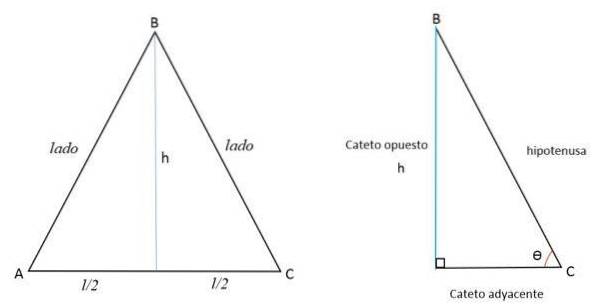
Como a altura é a linha perpendicular à base, ela a divide em duas partes iguais, estendendo-se até o vértice oposto. É assim que dois triângulos retângulos iguais são formados.
A altura (h) representa a perna oposta (a), metade do lado AC para a perna adjacente (b) e o lado BC representa a hipotenusa (c).
Usando o teorema de Pitágoras, o valor da altura pode ser determinado:
paradois + bdois = cdois
Onde:
paradois = altura (h).
bdois = lado b / 2.
cdois = lado a.
Substituindo esses valores no teorema de Pitágoras, e resolvendo pela altura, temos:
hdois + ( eu / dois)dois = eudois
hdois + eudois/ 4 = eudois
hdois = eudois - eudois/ 4
hdois = (4*eudois - eudois) / 4
hdois = 3*eudois /4
√hdois = √ (3*eudois /4)

Se o ângulo formado pelos lados congruentes for conhecido, a altura (representada por uma perna) pode ser calculada aplicando as razões trigonométricas.
As pernas são chamadas de opostas ou adjacentes, dependendo do ângulo tomado como referência..
Por exemplo, na figura acima, a perna h será oposta para o ângulo C, mas adjacente ao ângulo B:
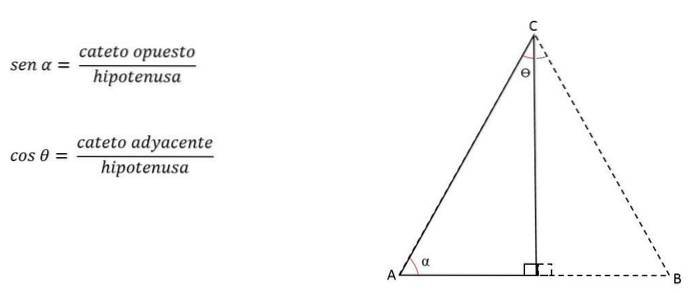
Assim, a altura pode ser calculada com:
Como calcular os lados?
Existem casos em que as medidas dos lados do triângulo não são conhecidas, mas sim a sua altura e os ângulos formados nos vértices.
Para determinar a área nestes casos é necessário aplicar as relações trigonométricas.
Conhecendo o ângulo de um de seus vértices, as pernas são identificadas e a razão trigonométrica correspondente é usada:
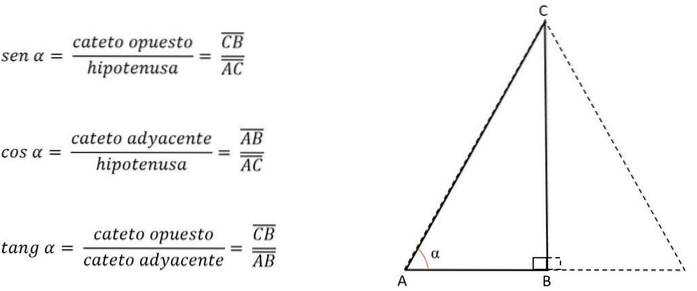
Assim, a perna AB será oposta para o ângulo C, mas adjacente ao ângulo A. Dependendo do lado ou perna correspondente à altura, o outro lado é desobstruído para obter o seu valor, sabendo que em um triângulo equilátero os três lados sempre terão a mesma medida.
Como calcular a área?
A área dos triângulos é sempre calculada com a mesma fórmula, multiplicando a base pela altura e dividindo por dois:
Área = (b * h) ÷ 2
Sabendo que a altura é dada pela fórmula:

Treinamento
- Primeiro exercício
Os lados de um triângulo equilátero ABC têm 20 cm cada. Calcule a altura e a área desse polígono.
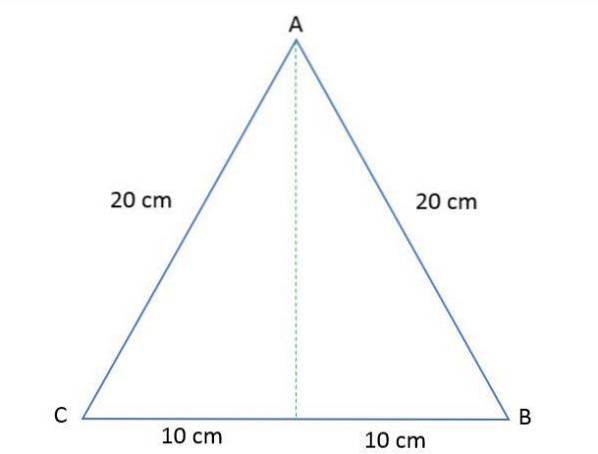
Solução
Para determinar a área deste triângulo equilátero é necessário calcular a altura, sabendo que ao desenhá-lo divide o triângulo em dois triângulos retângulos iguais.
Desta forma, o teorema de Pitágoras pode ser usado para encontrá-lo:
paradois + bdois = cdois
Onde:
a = 20/2 = 10 cm.
b = altura.
c = 20 cm.
Os dados são substituídos no teorema:
10dois + bdois = 20dois
100 cm + bdois = 400 cm
bdois = (400 - 100) cm
bdois = 300cm
b = √300 cm
b = 17,32 cm.
Ou seja, a altura do triângulo é igual a 17,32cm. Agora é possível calcular a área do triângulo dado, substituindo na fórmula:
Área = (b * h) ÷ 2
Área = (20 cm * 17,32 cm) ÷ 2
Área = 346,40 cmdois ÷ 2
Área = 173,20 cmdois.
Outra forma mais simples de resolver o exercício é substituindo os dados da fórmula direta pela área, onde o valor da altura também é encontrado implicitamente:

- Segundo exercício
As flores serão plantadas em um pedaço de terra que tem a forma de um triângulo equilátero. Se o perímetro desse terreno for igual a 450 m, calcule o número de metros quadrados que as flores vão ocupar.
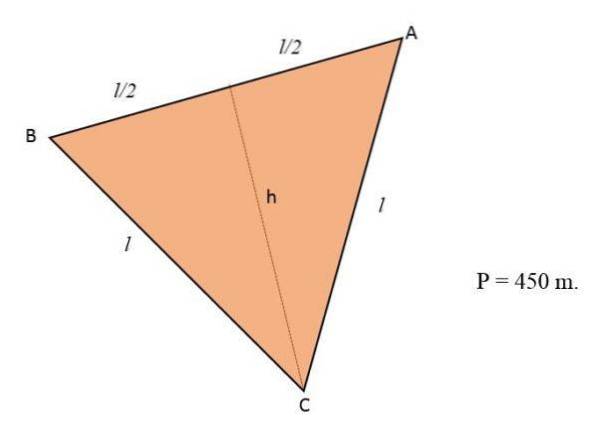
Solução
Sabendo que o perímetro de um triângulo corresponde à soma dos seus três lados e como o terreno tem a forma de um triângulo equilátero, os três lados deste terão a mesma medida ou comprimento:
P = lado + lado + lado = 3 * eu
3 * eu = 450 m.
l = 450 m ÷ 3
l = 150 m.
Agora só é necessário calcular a altura desse triângulo.
A altura divide o triângulo em dois triângulos retângulos congruentes, onde uma perna representa a altura e a outra metade a base. Pelo teorema de Pitágoras, a altura pode ser determinada:
paradois + bdois = cdois
Onde:
para = 150 m ÷ 2 = 75 m.
c = 150 m.
b = altura
Os dados são substituídos no teorema:
(75 m)dois + bdois = (150 m)dois
5.625 m + bdois = 22.500 m
bdois = 22.500 m - 5.625 m
bdois = 16.875 m
b = √16,875 m
b = 129,90 m.
Assim, a área que as flores ocuparão será:
Área = b * h ÷ 2
Área = (150 m * 129,9 m) ÷ 2
Área = (19.485 mdois) ÷ 2
Área = 9.742,5 mdois
- Terceiro exercício
O triângulo equilátero ABC é dividido por um segmento de reta que vai de seu vértice C até o ponto médio D, localizado no lado oposto (AB). Este segmento mede 62 metros. Calcule a área e o perímetro desse triângulo equilátero.
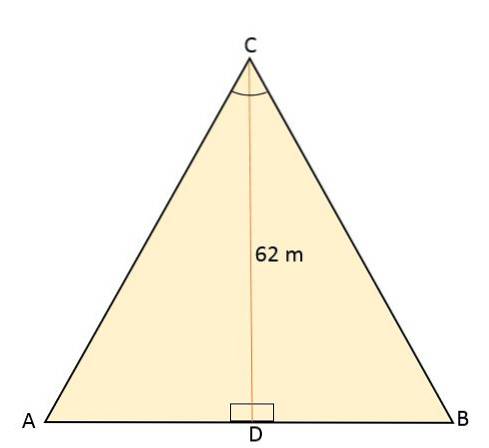
Solução
Sabendo que o triângulo equilátero é dividido por um segmento de reta que corresponde à altura, formando dois triângulos retos congruentes, este por sua vez também divide o ângulo do vértice C em dois ângulos com a mesma medida, 30ou cada um.
A altura forma um ângulo de 90ou em relação ao segmento AB, e o ângulo do vértice A irá então medir 60ou.
Então, usando o ângulo de 30 como referênciaou, a altura CD é definida como a perna adjacente ao ângulo e BC como a hipotenusa.
A partir desses dados, o valor de um dos lados do triângulo pode ser determinado, usando as razões trigonométricas:
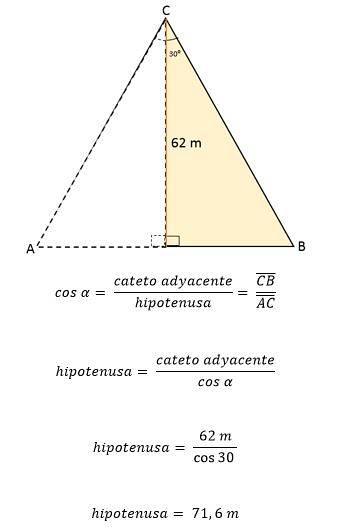
Como no triângulo equilátero todos os lados têm exatamente a mesma medida ou comprimento, isso significa que cada lado do triângulo equilátero ABC é igual a 71,6 metros. Sabendo disso, é possível determinar sua área:
Área = b * h ÷ 2
Área = (71,6 m * 62 m) ÷ 2
Área = 4.438,6 mdois ÷ 2
Área = 2.219,3 mdois
O perímetro é dado pela soma de seus três lados:
P = lado + lado + lado = 3 * eu
P = 3*eu
P = 3 * 71,6 m
P = 214,8 m.
Referências
- Álvaro Rendón, A. R. (2004). Desenho Técnico: livro de atividades.
- Arthur Goodman, L. H. (1996). Álgebra e trigonometria com geometria analítica. Pearson Education.
- Baldor, A. (1941). Álgebra. Havana: cultura.
- BARBOSA, J. L. (2006). Geometria Euclidiana plana. SBM. Rio de Janeiro, .
- Coxford, A. (1971). Geometria Uma Abordagem de Transformação. EUA: Laidlaw Brothers.
- Euclid, R. P. (1886). Elementos de geometria de Euclides.
- Héctor Trejo, J. S. (2006). Geometria e trigonometria.
- León Fernández, G. S. (2007). Geometria Integrada. Instituto Tecnológico Metropolitano.
- Sullivan, J. (2006). Álgebra e trigonometria. Pearson Education.



Ainda sem comentários