
Características do triângulo isósceles, fórmula e área, cálculo

UMA Triângulo isósceles é um polígono com três lados, onde dois deles têm a mesma medida e o terceiro lado uma medida diferente. Este último lado é chamado de base. Devido a essa característica foi dado esse nome, que em grego significa "pernas iguais"
Os triângulos são polígonos considerados os mais simples em geometria, porque são compostos de três lados, três ângulos e três vértices. São os que apresentam menor número de lados e ângulos em relação aos demais polígonos, porém seu uso é muito extenso.

Índice do artigo
- 1 Características dos triângulos isósceles
- 1.1 Componentes
- 2 propriedades
- 2.1 ângulos internos
- 2.2 Soma dos lados
- 2.3 Lados congruentes
- 2.4 Ângulos congruentes
- 2.5 Altura, mediana, bissetriz e bissetriz são coincidentes
- 2.6 Alturas relativas
- 2.7 Ortocentro, baricentro, incentivo e circuncentro coincidentes
- 3 Como calcular o perímetro?
- 4 Como calcular a altura?
- 5 Como calcular a área?
- 6 Como calcular a base do triângulo?
- 7 exercícios
- 7.1 Primeiro exercício
- 7.2 Segundo exercício
- 7.3 Terceiro exercício
- 8 referências
Características dos triângulos isósceles
O triângulo isósceles foi classificado usando a medida de seus lados como parâmetro, uma vez que dois de seus lados são congruentes (têm o mesmo comprimento)..
Com base na amplitude dos ângulos internos, os triângulos isósceles são classificados como:
- Triângulo retângulo isósceles: dois de seus lados são iguais. Um de seus ângulos está certo (90ou) e os outros são iguais (45ou cada um)
- Triângulo obtuso isósceles: dois de seus lados são iguais. Um de seus ângulos é obtuso (> 90ou).
- Triângulo agudo de isósceles: dois de seus lados são iguais. Todos os seus ângulos são agudos (< 90ou), onde dois têm a mesma medida.
Componentes (editar)
- Mediana: é uma linha que começa do ponto médio de um lado e atinge o vértice oposto. As três medianas convergem em um ponto denominado baricentro ou centróide..
- Bisector: é um raio que divide o ângulo de cada vértice em dois ângulos de igual medida. Por isso é conhecido como eixo de simetria e este tipo de triângulos possui apenas um.
- A mediadora: é um segmento perpendicular ao lado do triângulo, que tem sua origem no meio do triângulo. Existem três mediatices em um triângulo e eles se encontram em um ponto chamado circuncentro.
- A altura: é a linha que vai do vértice ao lado oposto e também esta linha é perpendicular a esse lado. Todos os triângulos têm três alturas, que coincidem em um ponto denominado ortocentro..
Propriedades
Os triângulos isósceles são definidos ou identificados porque possuem várias propriedades que os representam, originadas dos teoremas propostos por grandes matemáticos:
Ângulos internos
A soma dos ângulos internos é sempre igual a 180ou.
Soma dos lados
A soma das medidas de dois lados deve ser sempre maior que a medida do terceiro lado, a + b> c.
Lados congruentes
Os triângulos isósceles têm dois lados com a mesma medida ou comprimento; ou seja, eles são congruentes e o terceiro lado é diferente destes.
Ângulos congruentes
Os triângulos isósceles também são conhecidos como triângulos isoangulares, porque têm dois ângulos com a mesma medida (congruentes). Eles estão localizados na base do triângulo, opostos aos lados que têm o mesmo comprimento.
Devido a isso, foi gerado o teorema que afirma que:
"Se um triângulo tiver dois lados congruentes, os ângulos opostos a esses lados também serão congruentes." Portanto, se um triângulo é isósceles, os ângulos de suas bases são congruentes.
Exemplo:
A figura a seguir mostra um triângulo ABC. Desenhando sua bissetriz do vértice do ângulo B até a base, o triângulo é dividido em dois triângulos iguais BDA e BDC:
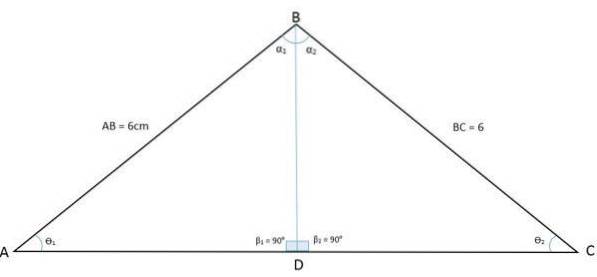
Desta forma, o ângulo do vértice B também foi dividido em dois ângulos iguais. A bissetriz é agora o lado comum (BD) entre esses dois novos triângulos, enquanto os lados AB e BC são os lados congruentes. Assim, temos o caso da congruência lado, ângulo, lado (LAL).
Isso mostra que os ângulos dos vértices A e C têm a mesma medida, assim como pode-se mostrar que como os triângulos BDA e BDC são congruentes, os lados AD e DC também são congruentes..
Altura, mediana, bissetriz e bissetriz são coincidentes
A linha que se traça do vértice oposto à base até o ponto médio da base do triângulo isósceles é ao mesmo tempo a altura, a mediana e a bissetriz, bem como a bissetriz em relação ao ângulo oposto da base..
Todos esses segmentos coincidem em um que os representa.
Exemplo:
A figura a seguir mostra o triângulo ABC com um ponto médio M que divide a base em dois segmentos BM e CM.
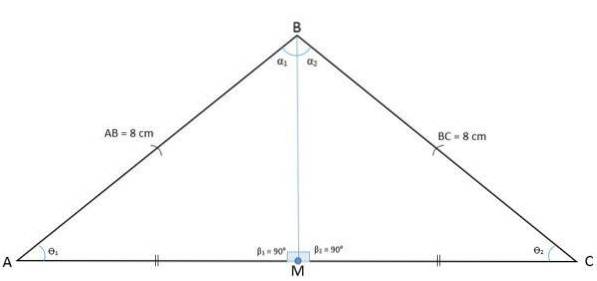
Desenhando um segmento do ponto M para o vértice oposto, por definição a mediana AM é obtida, que é relativa ao vértice A e lado BC.
Como o segmento AM divide o triângulo ABC em dois triângulos iguais AMB e AMC, isso significa que no caso de lado congruência, ângulo, lado será tido e, portanto, AM também será a bissetriz de BÂC.
Portanto, a bissetriz será sempre igual à mediana e vice-versa..
O segmento AM forma ângulos que têm a mesma medida para os triângulos AMB e AMC; ou seja, são complementares de tal forma que a medida de cada um será:
Med. (AMB) + Med. (AMC) = 180ou
dois * Med. (AMC) = 180ou
Med. (AMC) = 180ou ÷ 2
Med. (AMC) = 90ou
Pode-se saber que os ângulos formados pelo segmento AM em relação à base do triângulo são retos, o que indica que este segmento é totalmente perpendicular à base..
Portanto, representa a altura e a bissetriz, sabendo que M é o ponto médio.
Portanto, a linha AM:
- Representa no auge do BC.
- É de tamanho médio.
- Está contido na bissetriz de BC.
- É a bissetriz do ângulo do vértice Â
Alturas relativas
As alturas que são relativas a lados iguais também têm a mesma medida.
Como o triângulo isósceles tem dois lados iguais, suas duas alturas respectivas também serão iguais..
Ortocentro, baricentro, incentivo e circuncentro coincidente
Como a altura, mediana, bissetriz e bissetriz em relação à base, são representadas ao mesmo tempo pelo mesmo segmento, o ortocentro, baricentro central e circuncentro serão pontos colineares, ou seja, estarão na mesma linha:

Como calcular o perímetro?
O perímetro de um polígono é calculado adicionando os lados.
Como neste caso o triângulo isósceles tem dois lados com a mesma medida, seu perímetro é calculado com a seguinte fórmula:
P = 2*(lado a) + (lado b).
Como calcular a altura?
A altura é a linha perpendicular à base, ela divide o triângulo em duas partes iguais, uma vez que se estende até o vértice oposto.
A altura representa a perna oposta (a), o meio da base (b / 2) a perna adjacente e o lado “a” representa a hipotenusa.
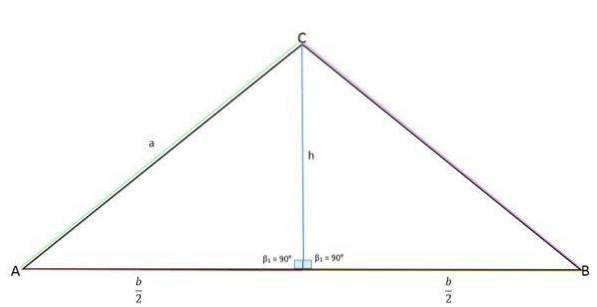
Usando o teorema de Pitágoras, o valor da altura pode ser determinado:
paradois + bdois = cdois
Onde:
paradois = altura (h).
bdois = b / 2.
cdois = lado a.
Substituindo esses valores no teorema de Pitágoras, e resolvendo pela altura, temos:
hdois + (b / dois)dois = paradois
hdois + bdois / 4 = paradois
hdois = paradois - bdois / 4
h = √ (paradois - bdois / 4).
Se o ângulo formado pelos lados congruentes for conhecido, a altura pode ser calculada com a seguinte fórmula:

Como calcular a área?
A área dos triângulos é sempre calculada com a mesma fórmula, multiplicando a base pela altura e dividindo por dois:

Há casos em que apenas são conhecidas as medidas de dois lados do triângulo e o ângulo formado entre eles. Neste caso, para determinar a área é necessário aplicar as relações trigonométricas:
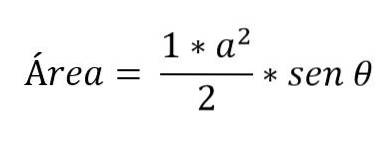
Como calcular a base do triângulo?
Como o triângulo isósceles tem dois lados iguais, para determinar o valor de sua base é necessário saber pelo menos a medida da altura ou um de seus ângulos.
Sabendo a altura, o teorema de Pitágoras é usado:
paradois + bdois = cdois
Onde:
paradois = altura (h).
cdois = lado a.
bdois = b / 2, é desconhecido.
Resolvemos para bdois da fórmula e temos que:
bdois = adois - cdois
b = √ adois - cdois
Como este valor corresponde à metade da base, deve ser multiplicado por dois para obter a medida completa da base do triângulo isósceles:
b = 2 * (√ adois - cdois)
Caso apenas o valor de seus lados iguais e o ângulo entre eles sejam conhecidos, a trigonometria é aplicada, desenhando uma linha do vértice até a base que divide o triângulo isósceles em dois triângulos retângulos.
Desta forma, metade da base é calculada com:

Também é possível que apenas o valor da altura e do ângulo do vértice oposto à base sejam conhecidos. Nesse caso, por trigonometria, a base pode ser determinada:

Treinamento
Primeiro exercício
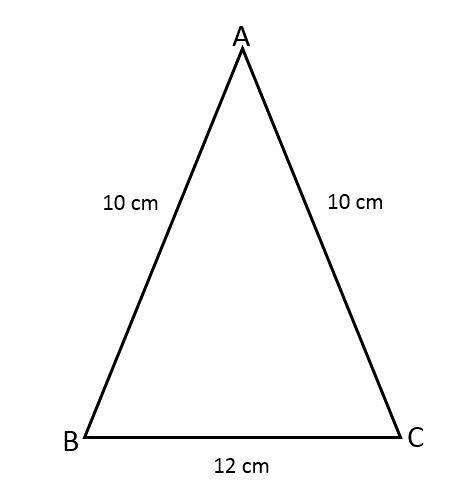
Encontre a área do triângulo isósceles ABC, sabendo que dois de seus lados têm 10 cm e o terceiro lado tem 12 cm.
Solução
Para encontrar a área do triângulo, é necessário calcular a altura usando a fórmula da área que está relacionada ao teorema de Pitágoras, pois o valor do ângulo formado entre os lados iguais não é conhecido.
Temos os seguintes dados do triângulo isósceles:
- Lados iguais (a) = 10 cm.
- Base (b) = 12 cm.
Os valores são substituídos na fórmula:

Segundo exercício
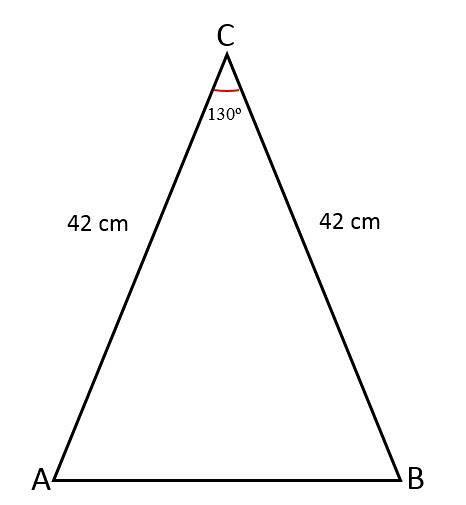
O comprimento dos dois lados iguais de um triângulo isósceles é de 42 cm, a união desses lados forma um ângulo de 130ou. Determine o valor do terceiro lado, a área desse triângulo e o perímetro.
Solução
Neste caso, as medidas dos lados e o ângulo entre eles são conhecidos..
Para saber o valor do lado que falta, ou seja, a base daquele triângulo, traça-se uma linha perpendicular a ele, dividindo o ângulo em duas partes iguais, uma para cada triângulo retângulo formado.
- Lados iguais (a) = 42 cm.
- Ângulo (Ɵ) = 130ou
Agora, por trigonometria, é calculado o valor da metade da base, que corresponde à metade da hipotenusa:
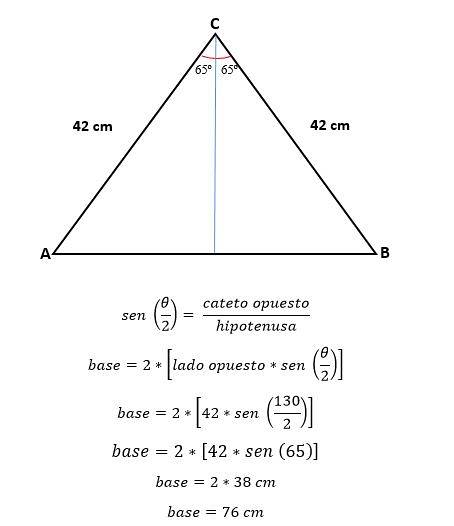
Para calcular a área é necessário saber a altura daquele triângulo que pode ser calculado por trigonometria ou pelo teorema de Pitágoras, agora que o valor da base já foi determinado.
Por trigonometria será:

O perímetro é calculado:
P = 2*(lado a) + (lado b).
P = 2* (42 cm) + (76 cm)
P = 84 cm + 76 cm
P = 160 cm.
Terceiro exercício
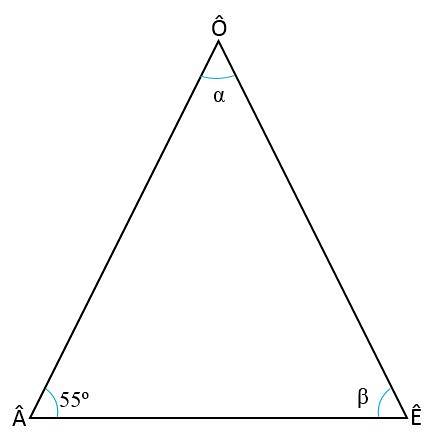
Calcule os ângulos internos do triângulo isósceles, sabendo que o ângulo da base é Â = 55ou
Solução
Para encontrar os dois ângulos ausentes (Ê e Ô), é necessário lembrar duas propriedades dos triângulos:
- A soma dos ângulos internos de cada triângulo será sempre = 180ou:
 + Ê + Ô = 180 ou
- Em um triângulo isósceles os ângulos da base são sempre congruentes, ou seja, têm a mesma medida, portanto:
 = Ô
Ê = 55ou
Para determinar o valor do ângulo Ê, substituímos os valores dos outros ângulos na primeira regra e resolvemos para Ê:
55ou + 55ou + Ô = 180 ou
110 ou + Ô = 180 ou
Ô = 180 ou - 110 ou
Ô = 70 ou.
Referências
- Álvarez, E. (2003). Elementos de geometria: com numerosos exercícios e geometria da bússola. Universidade de Medellin.
- Álvaro Rendón, A. R. (2004). Desenho Técnico: livro de atividades.
- Angel, A. R. (2007). Álgebra elementar. Pearson Education.
- Arthur Goodman, L. H. (1996). Álgebra e trigonometria com geometria analítica. Pearson Education.
- Baldor, A. (1941). Álgebra. Havana: cultura.
- José Jiménez, L. J. (2006). Matemática 2.
- Tuma, J. (1998). Manual de matemática de engenharia. Wolfram MathWorld.



Ainda sem comentários