
Características ovais (figura geométrica), exemplos, exercícios
O oval simétrica é definida como uma curva plana e fechada, que tem dois eixos perpendiculares de simetria - um maior e um menor - e é composta por dois arcos de circunferência iguais dois a dois.
Desta forma, pode ser traçado com o auxílio de um compasso e de alguns pontos de referência em uma das linhas de simetria. Em qualquer caso, existem várias maneiras de desenhá-lo, como veremos mais tarde.

É uma curva muito familiar, pois é reconhecida como o contorno de uma elipse, sendo este um caso particular da oval. Mas a oval não é uma elipse, embora às vezes se pareça muito com ela, pois suas propriedades e layout são diferentes. Por exemplo, a elipse não é construída com uma bússola.
Índice do artigo
- 1 recursos
- 2 exemplos
- 2.1 Construção de uma oval usando círculos concêntricos
- 3 exercícios
- 3.1 - Exercício 1
- 3.2 - Exercício 2
- 4 referências
Caracteristicas
O oval tem aplicações muito variadas: arquitetura, indústria, design gráfico, relojoaria e joalheria são apenas algumas áreas onde seu uso se destaca..
As características mais marcantes desta curva importante são as seguintes:
-Pertence ao grupo das curvas técnicas: é desenhada formando arcos circunferenciais com a ajuda de uma bússola.
-Todos os seus pontos estão no mesmo plano.
-Falta curvas ou loops.
-Seu layout é contínuo.
-A curva do oval deve ser lisa e convexa.
-Ao desenhar uma linha tangente ao oval, tudo está no mesmo lado da linha.
-Uma oval admite apenas duas tangentes paralelas no máximo.
Exemplos
Existem vários métodos de construção de formas ovais que requerem o uso de régua, esquadro e compasso. Em seguida, vamos mencionar alguns dos mais usados.
Construção de uma oval usando círculos concêntricos
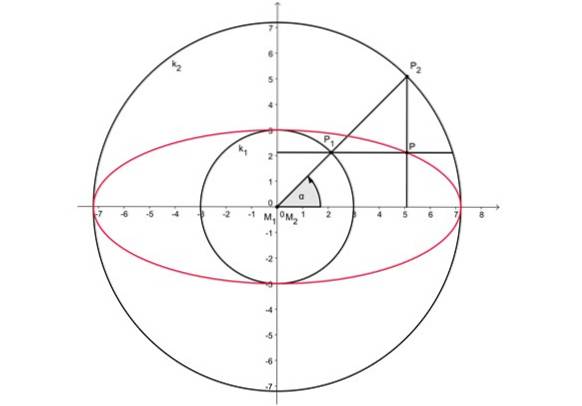
A Figura 2, acima, mostra dois círculos concêntricos centrados na origem. O eixo maior da oval mede o mesmo que o diâmetro da circunferência externa, enquanto o eixo menor corresponde ao diâmetro da circunferência interna.
-Um raio arbitrário é desenhado para a circunferência externa, que cruza os dois círculos nos pontos P1 E Pdois.
-Então o ponto P é projetadodois no eixo horizontal.
-Da mesma forma, o ponto P é projetado1 no eixo vertical.
-A intersecção de ambas as linhas de projeção é o ponto P e pertence ao oval.
-Todos os pontos nesta seção da oval podem ser plotados desta forma.
-O restante da oval é traçado com procedimento análogo, realizado em cada quadrante.
Treinamento
A seguir, serão examinadas outras formas de construção de ovais, dada uma certa medida inicial, que determinará seu tamanho..
- Exercício 1
Desenhe com a ajuda de uma régua e de um compasso uma oval, conhecida como seu eixo maior, cujo comprimento é de 9 cm.
Solução
Na Figura 3, mostrada abaixo, o oval resultante aparece em vermelho. Atenção especial deve ser dada às linhas pontilhadas, que são as construções auxiliares necessárias para desenhar uma oval cujo eixo principal é especificado. Vamos indicar todos os passos necessários para chegar ao desenho final.
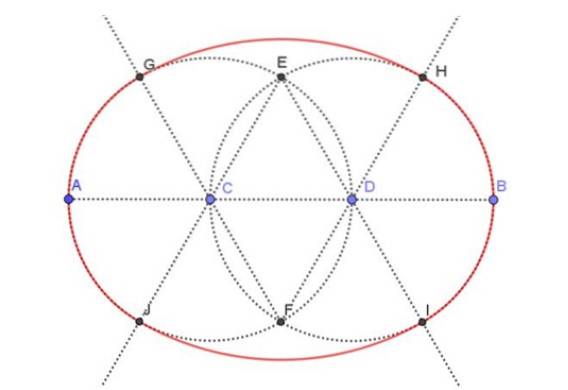
Passo 1
Desenhe com uma régua o segmento AB de 9 cm.
Passo 2
Trisect o segmento AB, ou seja, divida-o em três segmentos de igual comprimento. Uma vez que o segmento original AB é de 9 cm, os segmentos AC, CD e DB devem medir 3 cm cada um..
etapa 3
Com a bússola, centralizando em C e abrindo CA, uma circunferência auxiliar é desenhada. Da mesma forma, a circunferência auxiliar com centro D e raio DB é desenhada com a bússola..
Passo 4
As interseções dos dois círculos auxiliares construídos na etapa anterior são marcadas. Nós o chamamos de pontos E e F.
Etapa 5
Com a regra, os seguintes raios são desenhados: [FC), [FD), [EC), [ED).
Etapa 6
Os raios da etapa anterior cruzam os dois círculos auxiliares nos pontos G, H, I, J, respectivamente.
Etapa 7
Com o centro da bússola é feito em F e com a abertura (ou raio) FG o arco é desenhado GH. Da mesma forma, centrando em E e raio EI, o arco é desenhado EU J.
Etapa 8
A união dos arcos GJ, JI, IH Y HG forma uma oval cujo eixo principal é de 9 cm.
Etapa 9
Passamos a apagar (ocultar) os pontos e linhas auxiliares.
- Exercício 2
Desenhe uma oval com uma régua e compasso, cujo eixo menor é conhecido e sua medida é de 6 cm.
Solução
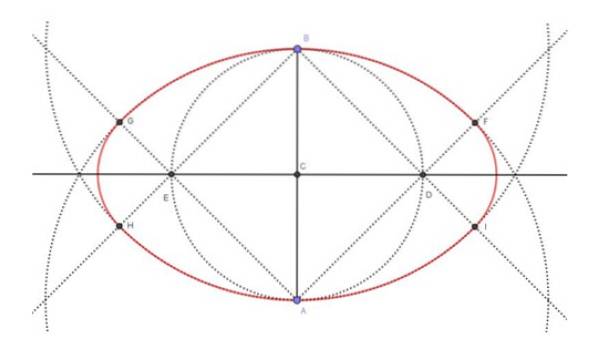
A figura acima (figura 4) mostra o resultado final da construção da oval (em vermelho), bem como as construções intermediárias necessárias para alcançá-la. As etapas seguidas para construir o oval de eixo menor de 6 cm foram as seguintes:
Passo 1
O segmento AB de 6 cm de comprimento é traçado com a régua.
Passo 2
Com a bússola e a régua, a bissetriz é traçada até o segmento AB.
etapa 3
A intersecção da bissetriz com o segmento AB, resulta no ponto médio C do segmento AB.
Passo 4
Com a bússola, a circunferência do centro C e raio CA é desenhada.
Etapa 5
A circunferência desenhada na etapa anterior cruza a bissetriz de AB nos pontos E e D.
Etapa 6
Os raios [AD), [AE), [BD) e [BE) são desenhados.
Etapa 7
Com a bússola, as circunferências do centro A e raio AB e do centro B e raio BA são desenhadas..
Etapa 8
As interseções dos círculos desenhados na etapa 7, com os raios construídos na etapa 6, determinam quatro pontos, a saber: F, G, H, I.
Etapa 9
Com o centro em D e o raio DI, o arco IF é desenhado. Da mesma forma, com centro em E e raio EG, o arco GH é desenhado.
Etapa 10
A união dos arcos de circunferência FG, GH, HI e IF determinam o oval desejado.
Referências
- Ed Plastic. Curvas técnicas: ovais, ovais e espirais. Recuperado de: drajonavarres.wordpress.com.
- Mathematische Basteleien. Curvas e ovais de ovo. Recuperado de: mathematische-basteleien.
- Universidade de Valência. Cônicas e curvas técnicas planas. Recuperado de: ocw.uv.es.
- Wikipedia. Oval. Recuperado de: es.wikipedia.org.
- Wikipedia. Oval. Recuperado de: en.wikipedia.org.



Ainda sem comentários