
Equação de direcionamento vetorial da linha, exercícios resolvidos
É compreendido por vetor diretor aquele que define a direção de uma linha, seja no plano ou no espaço. Portanto, um vetor paralelo à linha pode ser considerado um vetor direcionador da mesma.
Isso é possível graças a um axioma da geometria euclidiana que diz que dois pontos definem uma linha. Então, o segmento orientado formado por esses dois pontos também define um vetor diretor dessa linha.
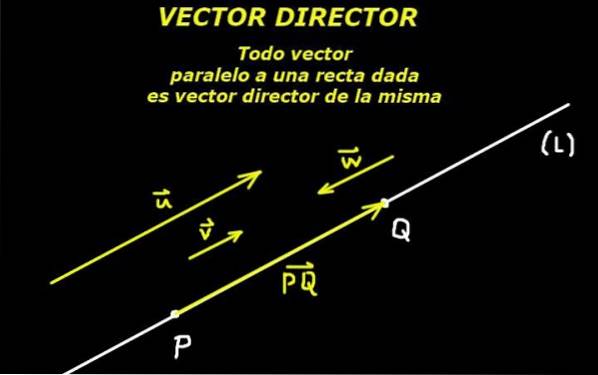
Dado um ponto P pertencendo à linha (EU) e dado um vetor diretor ou dessa linha, a linha é completamente determinada.
Índice do artigo
- 1 Equação da linha e vetor diretor
- 1.1 Equação paramétrica da linha
- 2 A linha em forma vetorial
- 2.1 Exemplo 2
- 2.2 Forma contínua da linha e do vetor diretor
- 3 Forma geral da equação da reta
- 3.1 Exemplo 3
- 4 Forma padrão da equação da linha
- 4.1 Exemplo 4
- 5 exercícios resolvidos
- 5.1 - Exercício 1
- 5.2 - Exercício 2
- 6 referências
Equação da linha e vetor diretor
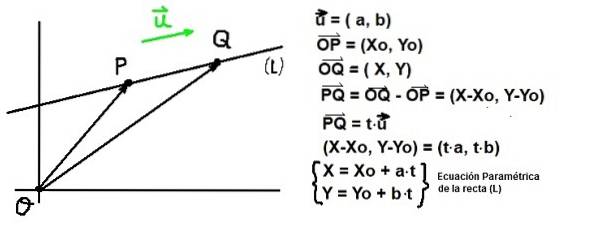
Dado um ponto P de coordenadas Q: (Xo, I) e um vetor ou diretor de uma linha reta (EU), todos os pontos Q de coordenadas Q: (X, Y) deve satisfazer que o vetor PQ ser paralelo a u. Esta última condição é garantida se PQ é proporcional a ou:
PQ = t⋅ou
na expressão anterior t é um parâmetro que pertence aos números reais.
Se os componentes cartesianos de PQ e de ou A equação acima é escrita da seguinte forma:
(X-Xo, Y-Yo) = t⋅ (a, b)
Se os componentes da igualdade do vetor forem equalizados, temos o seguinte par de equações:
X - Xo = a⋅t Y Y - I = b⋅t
Equação paramétrica da linha
As coordenadas X e Y de um ponto na linha (EU) passando por um ponto coordenado (Xo, I) e é paralelo a vetor diretor ou= (a, b) são determinados pela atribuição de valores reais ao parâmetro variável t:
X = Xo + a⋅t; Y = I + b⋅t
Exemplo 1
Para ilustrar o significado da equação paramétrica da linha, tomamos como o vetor de direção
ou = (a, b) = (2, -1)
e como um ponto conhecido da linha, o ponto
P = (Xo, I) = (1, 5).
A equação paramétrica da linha é:
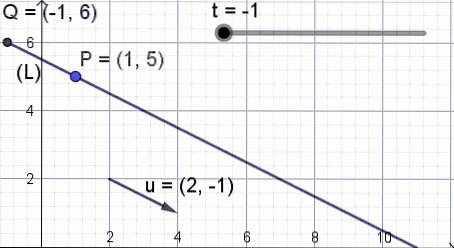
X = 1 + 2⋅t; Y = 5 - 1⋅t; -∞
Para ilustrar o significado desta equação, a figura 3 é mostrada, onde o parâmetro t muda de valor e o ponto Q de coordenadas (X, Y) tome posições diferentes na reta.
A linha em forma vetorial
Dado um ponto P na linha e seu vetor diretor u, a equação da linha pode ser escrita na forma vetorial:
OQ = OP + λ⋅ou
Na equação acima, Q é qualquer ponto, mas pertencente à linha e λ um número real.
A equação vetorial da linha é aplicável a qualquer número de dimensões, mesmo uma hiper-linha pode ser definida.
No caso tridimensional de um vetor diretor ou= (a, b, c) e um ponto P = (Xo, Yo, Zo), as coordenadas de um ponto genérico Q = (X, Y, Z) pertencente à linha é:
(X AND Z) = (Xo, Yo, Zo) + λ⋅ (a, b, c)
Exemplo 2
Considere novamente a linha que tem como vetor de direção
ou = (a, b) = (2, -1)
e como um ponto conhecido da linha, o ponto
P = (Xo, I) = (1, 5).
A equação vetorial desta linha é:
(X, Y) = (1, 5) + λ⋅ (2, -1)
Forma contínua da linha e do vetor diretor
Partindo da forma paramétrica, limpando e equacionando o parâmetro λ, temos:
(X-Xo) / a = (Y-Yo) / b = (Z-Zo) / c
Esta é a forma simétrica da equação da reta. Eu sinto isso para, b Y c são os componentes do vetor diretor.
Exemplo 3
Considere a linha que tem como vetor de direção
ou = (a, b) = (2, -1)
e como um ponto conhecido da linha, o ponto
P = (Xo, I) = (1, 5). Encontre sua forma simétrica.
A forma simétrica ou contínua da linha é:
(X - 1) / 2 = (Y - 5) / (- 1)
Forma geral da equação da reta
A equação que possui a seguinte estrutura é conhecida como a forma geral da reta no plano XY:
A⋅X + B⋅Y = C
A expressão para a forma simétrica pode ser reescrita para ter a forma geral:
b⋅X - a⋅Y = b⋅Xo - a⋅Yo
comparando com a forma geral da linha é:
A = b, B = -a e C = b⋅Xo - a⋅Yo
Exemplo 3
Encontre a forma geral da linha cujo vetor diretor é u = (2, -1)
e que passa pelo ponto P = (1, 5).
Para encontrar a forma geral, podemos usar as fórmulas fornecidas, no entanto, um caminho alternativo será escolhido.
Começamos encontrando o vetor dual w do vetor diretor u, definido como o vetor obtido trocando as componentes de u e multiplicando o segundo por -1:
C= (-1, -2)
o vetor dual C corresponde a uma rotação de 90 ° no sentido horário do vetor diretor v.
Nós multiplicamos escalarmente C com (X, Y) e com (Xo, I) e nós combinamos:
(-1, -2) • (X, Y) = (-1, -2) • (1, 5)
-X-2Y = -1 -2⋅5 = -11
permanecendo finalmente:
X + 2Y = 11
Forma padrão da equação da linha
É conhecida como a forma padrão da linha no plano XY, aquela que possui a seguinte estrutura:
Y = m⋅X + d
onde m representa a inclinação ed a interceptação com o eixo Y.
Dado o vetor de direção u = (a, b), a inclinação m é b / a.
Y d é obtido substituindo X e Y pelo ponto conhecido Xo, I:
I = (b / a) Xo + d.
Em suma, m = b / aed = I - (b / a) Xo
Observe que a inclinação m é o quociente entre o componente Y do vetor diretor e o componente x do mesmo.
Exemplo 4
Encontre a forma padrão da linha cujo vetor diretor é u = (2, -1)
e que passa pelo ponto P = (1, 5).
m = -½ e d = 5 - (-½) 1 = 11/2
Y = (-1/2) X + 11/2
Exercícios resolvidos
-Exercício 1
Encontre um vetor diretor da linha (L) que é a interseção do plano (Π): X - Y + Z = 3 e o plano (Ω): 2X + Y = 1.
Em seguida, escreva a forma contínua da equação da linha (L).
Solução
Da equação do plano (Ω) folga Y: Y = 1 -2X
Em seguida, substituímos na equação do plano (Π):
X - (1 - 2X) + Z = 3 ⇒ 3X + Z = 4 ⇒ Z = 4 - 3X
Em seguida, parametrizamos X, escolhemos a parametrização X = λ
Isso significa que a linha tem uma equação vetorial dada por:
(X, Y, Z) = (λ, 1 - 2λ, 4 - 3λ)
que pode ser reescrito como:
(X, Y, Z) = (0, 1, 4) + λ (1, -2, -3)
com o qual é claro que o vetor ou = (1, -2, -3) é um vetor de direção da linha (L).
A forma contínua da linha (L) é:
(X - 0) / 1 = (Y - 1) / (- 2) = (Z - 4) / (- 3)
-Exercício 2
Dado o plano 5X + para Y + 4Z = 5
e a linha cuja equação é X / 1 = (Y-2) / 3 = (Z -2) / (- 2)
Determine o valor de para de modo que o plano e a linha sejam paralelos.
Solução 2
O vetor n = (5, a, 4) é um vetor normal ao plano.
O vetor ou = (1, 3, -2) é um vetor diretor da linha.
Se a linha for paralela ao plano, então n • v = 0.
(5, para, 4)•(1, 3, -2) = 5 +3para -8 = 0 ⇒ para= 1.
Referências
- Fleming, W., & Varberg, D. E. (1989). Pré-cálculo Matemática. Prentice Hall PTR.
- Kolman, B. (2006). Álgebra Linear. Pearson Education.
- Leal, J. M., & Viloria, N. G. (2005). Geometria analítica plana. Mérida - Venezuela: Editorial Venezolana C. A.
- Navarro, Rocio. Vetores. Recuperado de: books.google.co.ve.
- Pérez, C. D. (2006). Pré-cálculo. Pearson Education.
- Prenowitz, W. 2012. Basic Concepts of Geometry. Rowman e Littlefield.
- Sullivan, M. (1997). Pré-cálculo. Pearson Education.


Ainda sem comentários